泰勒展开式真是个好东西。可以很方便的把一个函数展开成幂级数。即
从函数的线性近似 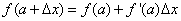
泰勒展开式了。这样的好东西,是怎么推导出来的呢?
在《直来直去微积分》看到了这个推导过程(在第10章,本文不是原创,只是一个学习笔记 ~_~)。
之前也思考了一下这个,但是没有什么太大的收获。现在知道了,原来是从微积分基本定理: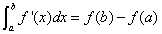
推导来的哦。
把上面微积分式子变形一下,
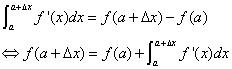
再做一个换元x=a+t,则dx=(a+t)'dt=dt。
接下来公式的整理,就交给你啦。~_~
泰勒公式余项”。~_~

文章标签 python泰勒级数展开求正弦 搜索 百度 文章分类 Python 后端开发
泰勒展开式真是个好东西。可以很方便的把一个函数展开成幂级数。即
从函数的线性近似 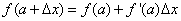
泰勒展开式了。这样的好东西,是怎么推导出来的呢?
在《直来直去微积分》看到了这个推导过程(在第10章,本文不是原创,只是一个学习笔记 ~_~)。
之前也思考了一下这个,但是没有什么太大的收获。现在知道了,原来是从微积分基本定理: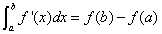
推导来的哦。
把上面微积分式子变形一下,
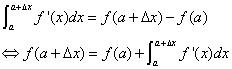
再做一个换元x=a+t,则dx=(a+t)'dt=dt。
接下来公式的整理,就交给你啦。~_~
泰勒公式余项”。~_~
MySQL优化
泰勒级数再讲傅立叶级数之前,我想先谈谈泰勒级数。因为傅立叶级数很大程度上与泰勒级数类似。 泰勒级数意义泰勒公式描述了任何初等函数都可以靠多项式拟合形成。具体点就是通过某一点的数值+导数+导数的导数,以此类推。举个常用的泰勒展开式 这个公式可以用来推导欧拉公式(待会要用) 泰勒公式推导由于 可以看到
举报文章
请选择举报类型
补充说明
0/200
上传截图
格式支持JPEG/PNG/JPG,图片不超过1.9M