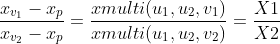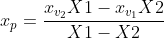小球反弹问题

51nod 1262 扔球

​​http://www.51nod.com/onlineJudge/questionCode.html#​​!problemId=1262

在圆上一点S，扔出一个球，这个球经过若干次反弹还有可能回到S点。N = 4时，有4种扔法，如图：

恰好经过4次反弹回到起点S（从S到T1，以及反向，共4种）。

给出一个数N，求有多少种不同的扔法，使得球恰好经过N次反弹，回到原点，并且在第N次反弹之前，球从未经过S点。

所有的分点。

画一个N=5的圆，它上面有6段不同的圆弧，球每一步跨越一个圆弧当然可以跑完所有的分点；当每一步跨越两个圆弧时，可以发现遗漏了一半的点；当每一步跨越三个圆弧时遗漏了4个点。发现规律：每一步跨越的步数i和N+1互质的话就符合条件，所以真相就是

#include <iostream>
#include <cstdio>
using namespace std;

int main()
{
    int n;
    while(~scanf("%d",&n)){
        int ans=n+1;
        int t=n+1;
        for(int i=2;i*i<=t;i++){
            if(t%i==0){
                ans=ans-ans/i;
                while(t%i==0) t/=i;
            }
        }
        if(t>1) ans=ans-ans/t;
        printf("%d\n",ans);
    }
    return 0;
}

HDU 3834 Where am I

此题没有AC，下面代码没有参考意义，仅供自己学习记录。（郁闷）

​​http://acm.hdu.edu.cn/showproblem.php?pid=3834​​

大意：一个小球在大环内运动，求解经过时间T后的位置。（会给出圆和球的参数，以及初始运动向量，整个过程没有能量损耗）

分析：

求解线段v1v2和u1u2的交点：

面积之比等于线段长度之比：

y坐标同理。

point intersection(point u1,point u2,point v1,point v2){
    double X1=xmulti(u1,u2,v1);
    double X2=xmulti(u1,u2,v2);  //xmulti是有向的，只要相交，
    point p;
    p.x=(v2.x*X1-v1.x*X2)/(X1-X2);
    p.y=(v2.y*X1-v1.y*X2)/(X1-X2);
    return p;
}

求解圆和直线的交点（已知有两交点）：

由已知的两点我们可以知道所在直线的向量，所以也能轻易地把法向量表示出来。

由此可以表示出cp线段，接着求出cp和p1p2的交点P. （得到P)

|cp1|=r，所以|pp1|能够求出，进一步:

同理求出p1.y和p2的坐标

void line_circle_intersec(point c,double r,point l1,point l2,point &p1,point &p2){
    point p=c;
    p.x+=l1.y-l2.y;
    p.y+=l2.x-l1.x;
    p=intersection(c,p,l1,l2);
    double p_l=sqrt(dis2(p,l1));
    double p_p=sqrt(r*r-dis2(c,p));
    double B=p_p/p_l;
    p1.x=(l1.x-p.x)*B+p.x;
    p1.y=(l1.y-p.y)*B+p.y;
    p_l=sqrt(dis2(p,l2));
    B=p_p/p_l;
    p2.x=(l2.x-p.x)*B+p.x;
    p2.y=(l2.y-p.y)*B+p.y;
}

再写得优雅一点：

void line_circle_intersec(point c,double r,point l1,point l2,point &p1,point &p2){
    point p=c;
    p.x+=l1.y-l2.y;
    p.y+=l2.x-l1.x;
    p=intersection(c,p,l1,l2);
    double l_l=sqrt(dis2(l1,l2));
    double p_p=sqrt(r*r-dis2(c,p));
    double B=p_p/l_l;
    p1.x=p.x+(l1.x-l2.x)*B;
    p1.y=p.y+(l1.y-l2.y)*B;
    p2.x=p.x+(l2.x-l1.x)*B;
    p2.y=p.y+(l2.y-l1.y)*B;
}

有了上诉技能，尝试解决此题：

由小球在环内碰撞运动的特殊性——相邻撞击点的距离是一定的，运动轨迹和半径的夹角是一定的，前后碰撞点和圆心成固定三角形。

由此，可先计算出T时间内的运动路程，然后根据“周期性”，找到最后的碰撞点，再依据所剩余的路程找到停止点。

然而，不知道为何就是WA啊啊啊啊。。

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-10;
struct point{
    double x,y;
    point(double _x=0,double _y=0):x(_x),y(_y){}
    void show(){
        printf("%.1lf %.1lf\n",x,y);
    }
};
double xmulti(point p0,point p1,point p2){
    return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);
}
double dis2(point p1,point p2){
    return (p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y);
}
point intersection(point u1,point u2,point v1,point v2){
    double X1=xmulti(u1,u2,v1);
    double X2=xmulti(u1,u2,v2);  //xmulti是有向的，只要相交，
    point p;
    p.x=(v2.x*X1-v1.x*X2)/(X1-X2);
    p.y=(v2.y*X1-v1.y*X2)/(X1-X2);
    return p;
}
void line_circle_intersec(point c,double r,point l1,point l2,point &p1,point &p2){
    point p=c;
    p.x+=l1.y-l2.y;
    p.y+=l2.x-l1.x;
    p=intersection(c,p,l1,l2);
    double l_l=sqrt(dis2(l1,l2));
    double p_p=sqrt(r*r-dis2(c,p));
    double B=p_p/l_l;
    p1.x=p.x+(l1.x-l2.x)*B;
    p1.y=p.y+(l1.y-l2.y)*B;
    p2.x=p.x+(l2.x-l1.x)*B;
    p2.y=p.y+(l2.y-l1.y)*B;
}
// 已知圆上一点和逆时针旋转圆心角，求解对称点
/*point rotated(point c,point p,double angle){  //angle是逆时针圆心角度数，P是原点，C是圆心
    p.x-=c.x;
    p.y-=c.y;
    c.x+=p.x*cos(angle)-p.y*sin(angle);
    c.y+=p.x*sin(angle)+p.y*cos(angle);
    return c;
}*/
point rotated(point c,point p,double angle){  //angle是逆时针圆心角度数，P是原点，C是圆心
    p.x-=c.x;
    p.y-=c.y;
    double t1=cos(angle)*1.0;
    double t2=sin(angle)*1.0;
    c.x+=p.x*t1-p.y*t2; //坐标旋转  点逆时针跑产生的增量向量相当于顺时针方向增加坐标值
    c.y+=p.x*t2+p.y*t1;
    return c;
}

int main()
{
    //freopen("cin.txt","r",stdin);
    int N;
    point O,A,vec;
    double R,r,t;
    cin>>N;
    while(N--){
        scanf("%lf%lf%lf",&O.x,&O.y,&R);
        scanf("%lf%lf%lf",&A.x,&A.y,&r);
        scanf("%lf%lf%lf",&vec.x,&vec.y,&t);

        point ans;
        double len=sqrt(vec.x*vec.x+vec.y*vec.y)*t;
        point p1,p2;
        point pc1;
        line_circle_intersec(O,R-r,A,point(A.x+vec.x,A.y+vec.y),p1,p2);
        //if(fabs((p1.x-A.x)*vec.y - (p1.y-A.y)*vec.x)<eps) pc1=p1;
        if((p1.x-A.x)*vec.x>=0&&(p1.y-A.y)*vec.y>=0) pc1=p1;
        else pc1=p2;

        double limit=sqrt(dis2(A,pc1));
        if(len-limit<=-eps) {
            ans.x=A.x+vec.x*t;
            ans.y=A.y+vec.y*t;
            ans.show();
            continue;
        }

        len=len-limit;
        double line_len=sqrt(dis2(p1,p2));
        int sum=(int)(len/line_len);
        R=R-r;
        double cosx=(2*R*R-line_len*line_len)/(2*R*R);
        double angle1=acos(cosx);
        if(xmulti(O,A,pc1)<eps)  angle1=-angle1;
        point pc2=rotated(O,pc1,sum*angle1);
        len=len-line_len*sum;
        double B=len/line_len;
        //point pc3=rotated(O,pc2,angle1);
        point pc3=rotated(O,pc1,(sum+1)*angle1);
        ans.x=pc2.x+(pc3.x-pc2.x)*B;
        ans.y=pc2.y+(pc3.y-pc2.y)*B;
        ans.show();
    }
    return 0;
}