字符串之KMP算法

KMP有什么用?

KMP主要应用在字符串匹配上。

KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

所以如何记录已经匹配的文本内容，是KMP的重点，也是next数组肩负的重任。

Next[]数组是什么?

而Next[]数组存放的是什么?-----最长公共前后缀,也就是一个前缀表.
当我们获得了模式串的前缀表,我们匹配字符串就可以这样(如下图所示),当匹配到不相等的,就跳至当前子串的最长公共前缀的下一个位置.

为什么这样呢?因为子串的公共前后缀是相等的,文本串移动到i位置,说明之前的公共后缀已经匹配通过了,而该公共后缀又和模式串的公共前缀相同.所以下一次文本串直接从上一次不匹配的开始,模式串直接从公共前缀的下一个字符开始匹配.

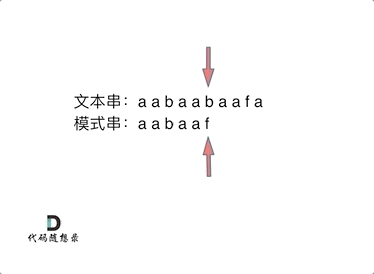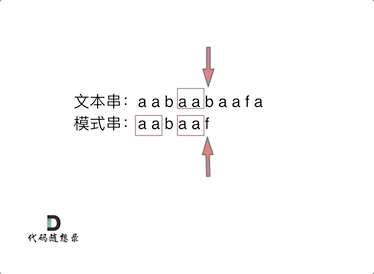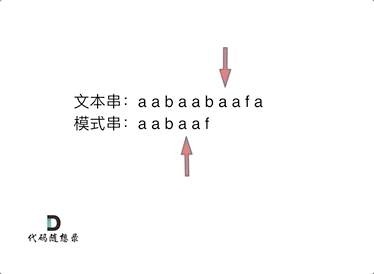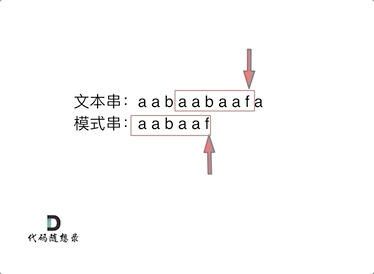
以上就是我们为什么要求模板串的最长公共前后缀.

Next[]如何求呢?

分为四步:

• 初始化next数组和变量
  Next[0] = 0,i = 0;j=1
• 当s[i] != s[j]时
  j要跳到next[j-1]的位置.继续进行比较,直到相等或者j <= 0退出循环.
• 当s[i]=s[j],说明当前字符可以作为公共前后缀的一部分.j++
• Next[]数组进行赋值:Next[i] = j

每一步的图解如下:

实现代码:

void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }

进行字符串匹配过程

思路分析:

匹配过程与求Next[]数组很相似.

• 第一步:使用j指向模板串,i指向文本串.
• 如果haystack[i]=needle[j],i++,j++
• 如果haystack[i] != needle[j],j= next[j - 1], 直到相等或者 j<=0.
• 判断j 是否等于了needle.size(),如果等,则说明已经匹配到了子串,否则说明还在进行中.
• 如果i的循环执行完了还没有匹配到,说明haystack中不存在子串needle.返回-1.

实现代码

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    //haystack:文本串  needle:模板串
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = 0;
        for (int i = 0; i < haystack.size(); i++) {
            while(j > 0 && haystack[i] != needle[j]) {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == needle.size() ) {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

​​以上思路参考自卡尔大佬的代码随想录​​