转自leetcode:
https://leetcode-cn.com/explore/featured/card/array-and-string/200/introduction-to-string/1429/

字符串匹配算法：KMP

Knuth–Morris–Pratt（KMP）算法是一种改进的字符串匹配算法，它的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。它的时间复杂度是 O(m+n)。

这段话你可能并不理解。没关系，我们来看一个例子。

情景 1

假如你是一名生物学家，现在，你的面前有两段 DNA 序列 S 和 T，你需要判断 T 是否可以匹配成为 S 的子串。

字符串匹配算法：KMP_字符串

你可能会凭肉眼立即得出结论：是匹配的。可是计算机没有眼睛，只能对每个字符进行逐一比较。

对于计算机来讲，首先它会从左边第一个位置开始进行逐一比较：

字符串匹配算法：KMP_后缀_02

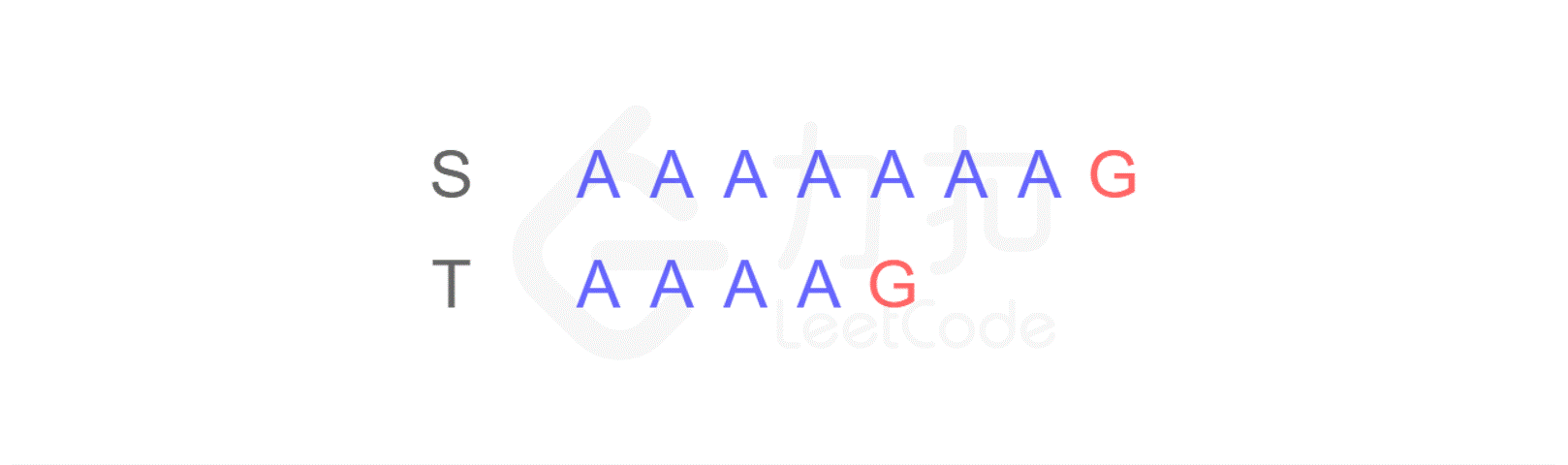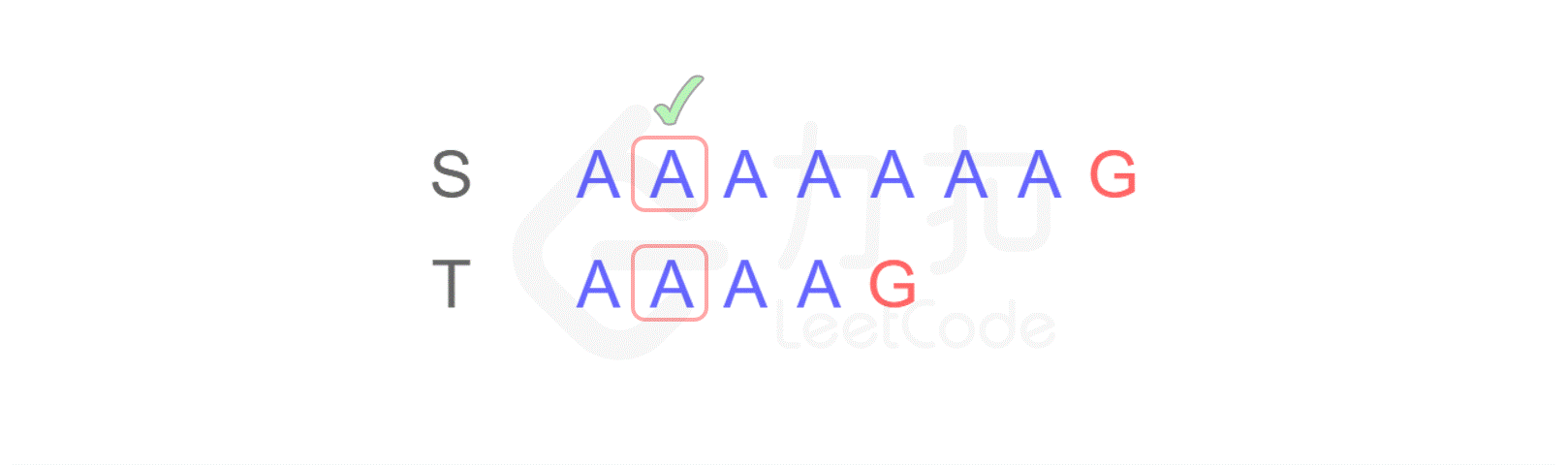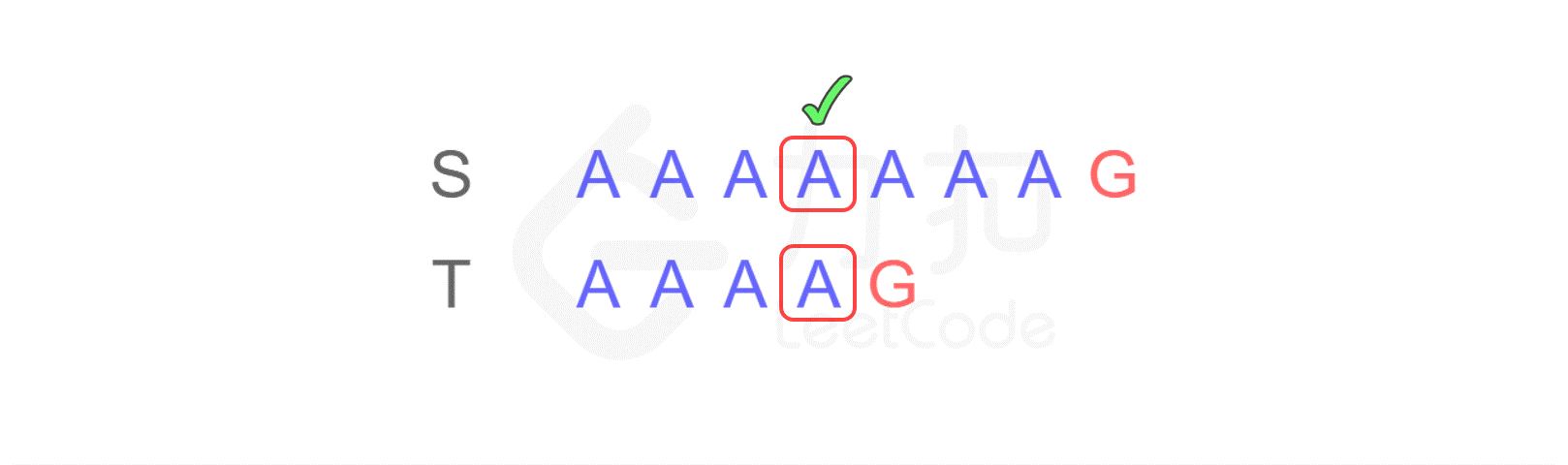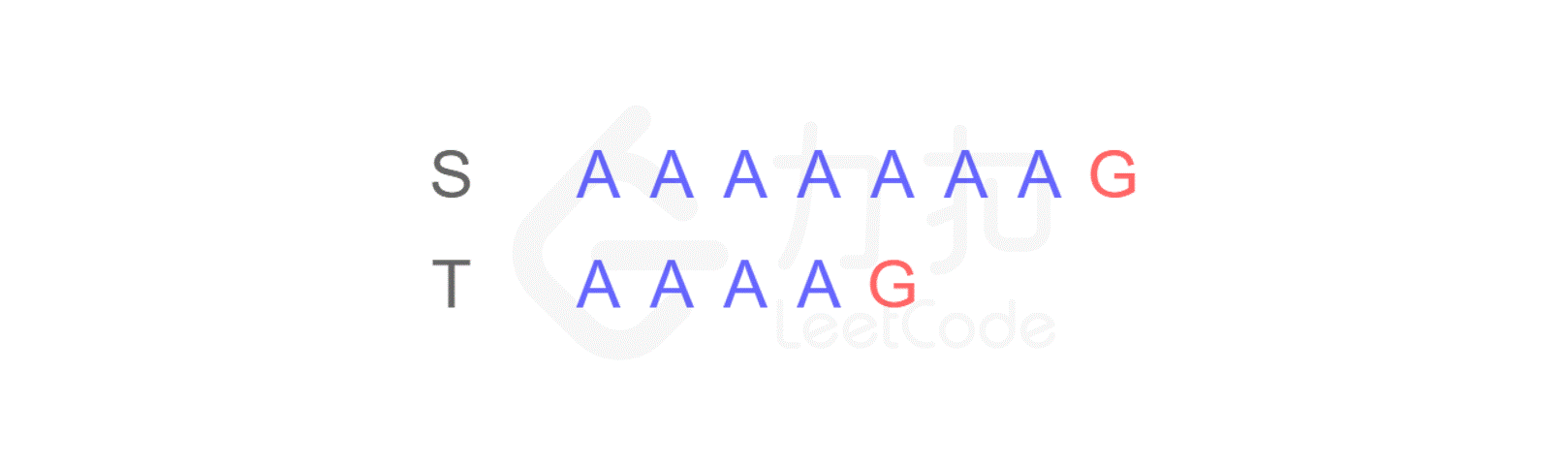
这样，当匹配到 T 的最后一个字符时，发现不匹配，于是从 S 的第二个字符开始重新进行比较：

字符串匹配算法：KMP_后缀_03

仍然不匹配，再次将 T 与 S 的第三个字符开始匹配…不断重复以上步骤，直到从 S 的第四个字符开始时，最终得出结论：S 与 T 是匹配的。

字符串匹配算法：KMP_字符串_04

你发现这个方法的弊端了吗？我们在进行每一轮匹配时，总是会重复对 A 进行比较。也就是说，对于 S 中的每个字符，我们都需要从 T 第一个位置重新开始比较，并且 S 前面的 A 越多，浪费的时间也就越多。假设 S 的长度为  m，T 的长度为  n，理论上讲，最坏情况下迭代 m−n+1 轮，每轮最多进行 n 次比对，一共比较了 (m−n+1)×n 次，当 m>>n 时，渐进时间复杂度为  O(mn)。

而 KMP 算法的好处在于，它可以将时间复杂度降低到 O(m+n)，字符序列越长，该算法的优势越明显。它是怎么实现的呢？

情景 2

再来举一个例子，现在有如下字符串 S 和 P，判断 P 是否为 S 的子串。

字符串匹配算法：KMP_后缀_05

我们仍然按照原来的方式进行比较，比较到 P 的末尾时，我们发现了不匹配的字符。

字符串匹配算法：KMP_后缀_06

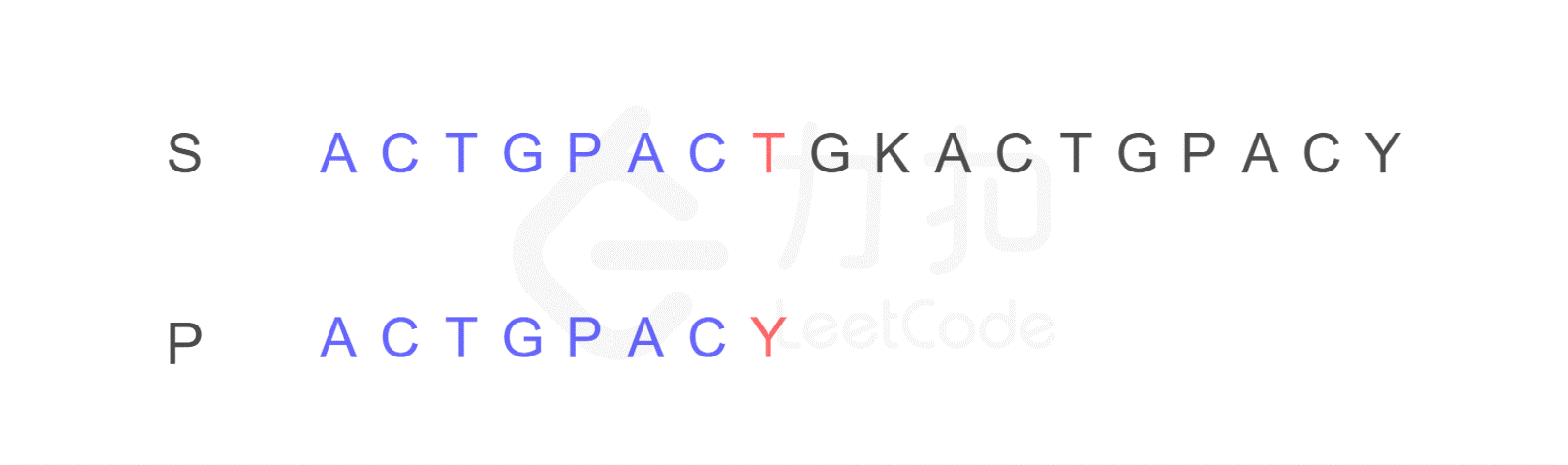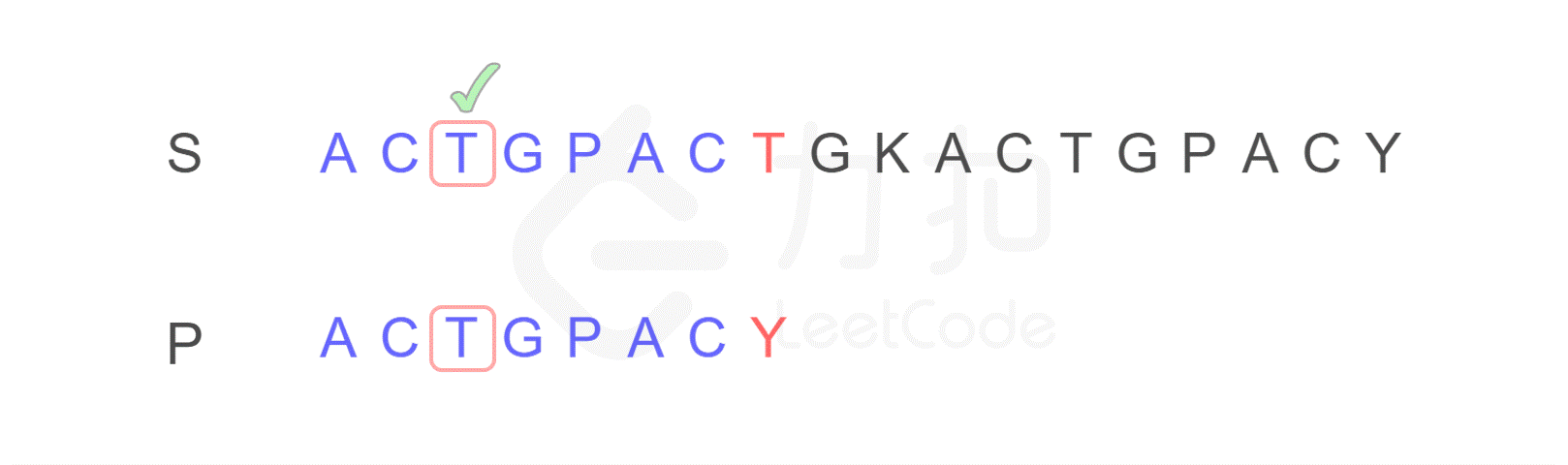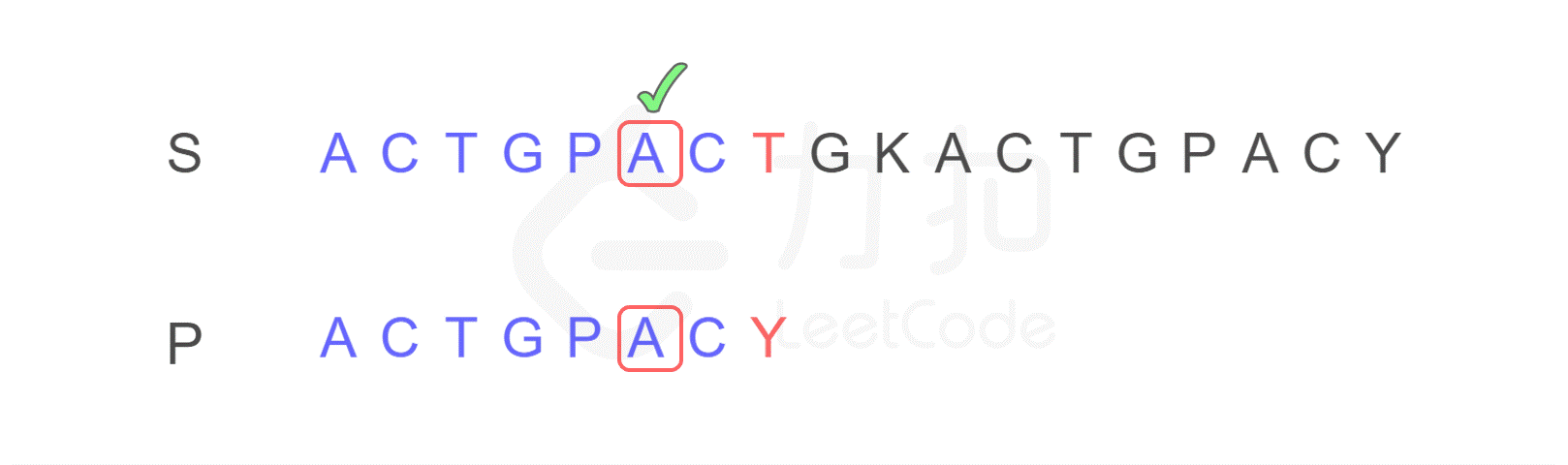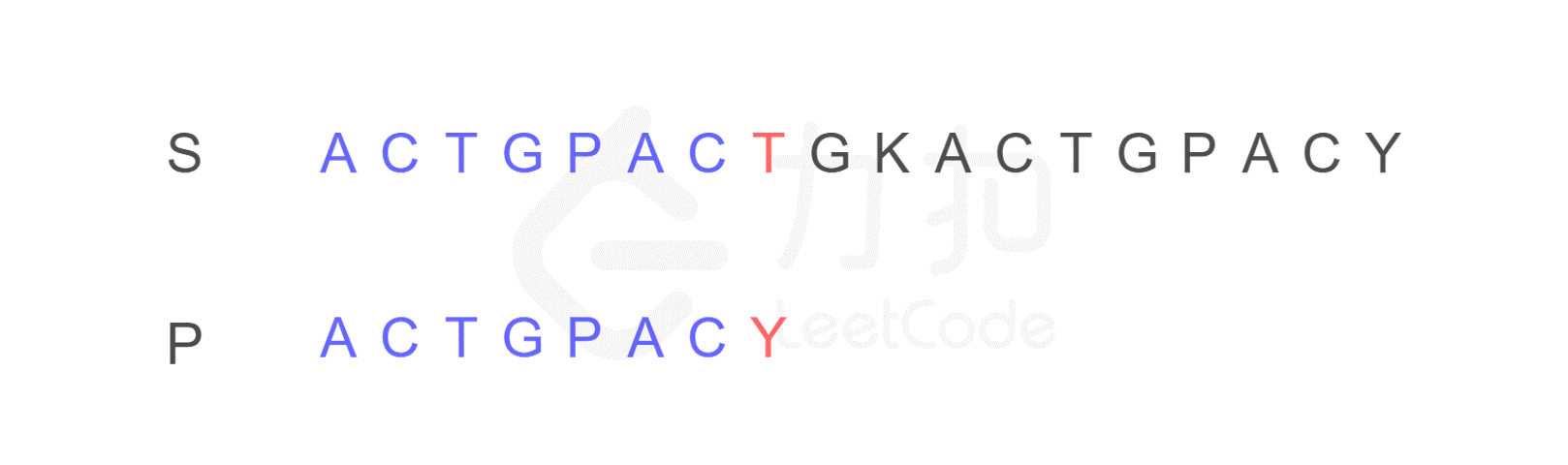
注意，按照原来的思路，我们下一步应将字符串 P 的开头，与字符串 S 的第二位 C 重新进行比较。而 KMP 算法告诉我们，我们只需将字符串 P 需要比较的位置重置到图中 j 的位置，S 保持 i 的位置不变，接下来即可从 i，j 位置继续进行比较。

字符串匹配算法：KMP_后缀_07

为什么？我们发现字符串 P 有子串 ACT 和 ACY，当 T 和 Y 不匹配时，我们就确定了 S 中的蓝色 AC 并不匹配 P 右侧的 AC，但是可能匹配左侧的 AC，所以我们从位置 i 和 j 继续比较。

换句话说，Y 对应下标 2，表示下一步要重新开始的地方。

既然如此，如果每次不匹配的时候，我们都能立刻知道 P 中不匹配的元素，下一步应该从哪个下标重新开始，这样不就能大大简化匹配过程了吗？这就是 KMP 的核心思想。

KMP 算法中，使用一个数组 next 来保存 P 中元素不匹配时，下一步应该重新开始的下标。由于计算机不能像我们人类一样，通过视觉来得出结论，因此这里有一种适合计算机的构造 next 数组的方法。

小插曲：构造 next 数组

构造方法为：P[i] 对应的下标，为 P[0...i + 1] 的最长公共前缀后缀的长度，令 P[0] = -1。 具体解释如下：

例如对于字符串 abcba：

  • 前缀：它的前缀包括：a, ab, abc, abcb，不包括本身；
  • 后缀：它的后缀包括：bcba, cba, ba, a，不包括本身；
  • 最长公共前缀后缀：abcba 的前缀和后缀中只有 a 是公共部分，字符串 a 的长度为 1。

所以，我们将 P[0...i + 1] 的最长公共前后缀的长度作为 P[i] 的下标，就得到了 next 数组。

字符串匹配算法：KMP_后缀_08

回到情景 2

我们将思绪切换回来，上次我们还停留在位置 i 和 j，现在继续进行比较。从如下图所示，由于我们已经构造了 next 数组，当继续移动到图中的 r 和 c 位置时，发现不匹配，根据 next 数组，我们可以立即将位置 c 回到下标 0 的位置：

字符串匹配算法：KMP_字符串_09

之后的情形就很简单了：

  • K 与 A 不匹配，查看 next 数组，A 对应 next 中的元素为 -1，表示不动，r 加 1；
  • 位置 r 字符与位置 c 字符匹配，继续比较下一位；
  • 后面元素均匹配，最终找到匹配元素。

以上就是 KMP 算法的思想，现在回过头来看文章开头的第一句话，你是否有更加深刻的理解了呢？

结尾

最后，我们给出相关代码。

KMP 主算法参考代码：

int match (char* P, char* S){ // KMP 算法
    int* next = buildNext(P); // 构造 next 表
    int m = (int) strlen (S), i = 0; // 文本串指针
    int n = (int) strlen(P), j = 0; //模式串指针
    while (j < n && i < m) // 自左向右逐个比对字符
        if (0 > j || S[i] == P[j]) // 若匹配，或 P 已移除最左侧
            {i++; j++} // 则转到下一字符
        else
            j = next[j]; // 模式串右移（注意：文本串不用回退）
    delete [] next; // 释放 next 表
    return i - j;
}

构造 next 表参考代码：

int* buildNext(char* P) { // 构造模式串 P 的 next 表
   size_s m = strlen(P), j = 0; // “主”串指针
   int* N = new int[m]; // next 表
   int  t = N[0] = -1; // 模式串指针
   while (j < m - 1)
       if ( 0 > t || P[j] == P[t]){ // 匹配
           j++; t++;
           N[j] = t; // 此句可改进为 N[j] = (P[j] != P[t] ? t : N[t]);
       }else // 失配
       t = N[t];
   return N;

}