前缀和&差分

转载

mob604756f8c81a 2021-08-03 16:17:33

前缀和&差分

前缀和是一个数组在某个下标之前的所有数组元素之和（包括此元素）。
差分是将数列中的每一项分别与前一项做差。

一维前缀和

定义式：\(b[i] = \sum_{j=0}^{i}a[j]\)；
递推公式：\(b[0]=0; b[i] = b[i-1]+a[i]\);

初始化O(n):

for(int i = 1; i <= n; i++){
	cin >> a[i];
	b[i] = b[i-1]+a[i];
}

查询O(1):

cout << b[l] - b[r-1] << endl;

上道例题 AT1894総和

输入两个整数\(n,k\)，给出一个长度为\(n\)数列，求这个数列中的所有长度为\(k\)的连续的部分的总和。\(1 \leq k \leq n \leq 10^5,0 \leq a_i \leq 10^8\)。

思路：本题数据范围过大，我们无法使用暴力，我们可以先计算整个数列的前缀和，然后计算数列中的所有长度为\(k\)的连续的部分的总和。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl '\n'
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
const int INF = 0x7fffffff;
const int N = 1e5+10;

ll arr[N], n, k, res;

int main(){
	cin >> n >> k;
	for(int i = 1; i <= n; i++){
		cin >> arr[i];
		arr[i] += arr[i-1];
	}
	for(int i = 1; i <= n-k+1; i++){
		res += arr[k+i-1] - arr[i-1];
	}
	cout << res << endl;
	return 0;
}

一维差分

例如\(A:1，2，3，4，5，6\)，差分后是\(B:1，1，1，1，1，1\)。
所以我们可以知道，对于一个给定的数列\(A[]\)，它的差分数列\(B[]\)为：\(B[1] = A[1]，B[i] = A[i] - A[i-1]\)。（数列\(A[]\)是数列\(B[]\)的前缀和）

单点修改：\(A[i]+num\)。
若将\(A[2]+1\)，则\(A:1,3,3,4,5,6\quad B:1,2,0,1,1,1\)。
所以我们发现单点修改，只要改变差分数列中的自己和后一个数即可（即\(A[i]+num,A[i+1]-num\)）

区间修改：区间\([L,R]\)增加\(num\)。
若将\(A\)数组\([2,5]\)每个元素增加1，则\(A:1,3,4,5,6,6 \quad B:1,2,1,1,1,0\)。
所以我们发现区间修改，只需要改变\(B[L]\)和\(B[R+1]\)即可（即\(A[L]+num,A[R+1]-num\)）

同样上道例题 CF44C

\(n\)天假期，安排\(m\)个人来浇花，第\(i\)个人负责\(a[i],b[i]\)天，问花是否可以每天都被浇水且不重复。可以的话输出“\(OK\)”，不可以的话输出最早出问题的那天的天号以及那天花被浇了多少次水。\(1\leq n,m \leq 100 \quad 1 \leq a[i] \leq b[i] \leq n \quad b[i] \leq a[i+1]\)。

思路：这道题的数据范围很小，我们使用暴力也是可以解决的，但在这里我们还是使用一维差分的思想。那么我们应该如何实现？很简单，我们只需要开一个数组，对它进行区间修改（即在\(arr[l]\)上加\(1\)表示浇过一天水，再在\(arr[r+1]\)上减去\(1\)表示到这一天截止），最后从头到尾遍历一遍，\(arr[i]+=arr[i-1]\)即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl '\n'
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
const int INF = 0x7fffffff;
const int N = 1e5+10;

int arr[N], n, m, l, r;

int main(){
	cin >> n >> m;
	for(int i = 1; i <= m; i++){
		cin >> l >> r;
		arr[l] += 1;
		arr[r+1] -= 1;//做差分
	}
	for(int i = 1; i <= n; i++){
		arr[i] += arr[i-1];
		if(arr[i] != 1){
			cout << i << " " << arr[i] << endl;
			return 0; 
		}
	}
	cout << "OK" << endl;
	return 0;
}

二维前缀和

定义式：\(b[x][y]=\) \(\sum_{i=0}^{x}\sum_{j=0}^{y}a[i][j]\)
递推公式：\(b[x][y]=b[x-1][y]+b[x][y-1]-b[x-1][y-1]+a[x][y]\)

初始化O(nm):

for(int i = 1; i <= n; i++){
	for(int j = 1; j <= m; j++){
		cin >> a[i][j];
		b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j];
	}
}

下面我们来理解为什么二维前缀和的递推公式为\(b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j]\)。

原数组A	\(2_{1,1}\)	\(3_{1,2}\)	\(4_{1,3}\)	前缀和B	\(2_{1,1}\)	\(5_{1,2}\)	\(9_{1,3}\)
	\(7_{2,1}\)	\(4_{2,2}\)	\(8_{2,3}\)		\(9_{2,1}\)	\(16_{2,2}\)	\(28_{2,3}\)
	\(5_{3,1}\)	\(9_{3,2}\)	\(10_{3,3}\)		\(14_{3,1}\)	\(30_{3,2}\)	\(52_{3,3}\)

现在我们来计算区间\(A[2][2]\)的前缀和：
如果我们直接用递推公式\(B[2][2]=B[2][1]+B[1][2]-A[1][1]+A[2][2]=9+5-2+4=16\);为什么呐？
\(B[2][2]=A[1][1]+A[1][2]+A[2][1]+A[2][2]=2+3+7+4=16\);
\(B[2][1]=A[1][1]+A[2][1]\);
\(B[1][2]=A[1][1]+A[1][2]\);
使用在我们计算\(A[2][2]\)前缀和的时候就可以用\(A[1][2]\)的前缀和加上\(A[2][1]\)的前缀和，再减去多加的\(A[1][1]\)，最后加上自己本身的数值。

查询O(1):

sum = b[x2][y2] - b[x2][y1-1] - b[x1-1][y2] + b[x1-1][y1-1];

同样的下面我们来理解二维前缀和的查询代码：

原数组A	\(2_{1,1}\)	\(3_{1,2}\)	\(4_{1,3}\)	前缀和B	\(2_{1,1}\)	\(5_{1,2}\)	\(9_{1,3}\)
	\(7_{2,1}\)	\(4_{2,2}\)	\(8_{2,3}\)		\(9_{2,1}\)	\(16_{2,2}\)	\(28_{2,3}\)
	\(5_{3,1}\)	\(9_{3,2}\)	\(10_{3,3}\)		\(14_{3,1}\)	\(30_{3,2}\)	\(52_{3,3}\)

现在我们想求区间\(A[2][3]\)到\(A[3][3]\)的数值之和\(res\)：
如果我们直接使用代码\(res=B[3][3]-B[3][2]-B[1][3]+B[1][2]=52-30-9+5=18\);Why?
我们来看\(B[3][3]\)等于区间\(A[1][1]\)到\(A[3][3]\)的和，\(B[2][3]\)等于区间\(A[1][1]\)到\(A[2][3]\)的和
现在我们计算区间\(A[2][3]\)到\(A[3][3]\)的和，就等于我们在区间\(A[1][1]\)到\(A[3][3]\)上删除区间\(A[1][1]\)到\(A[3][2]\)和区间\(A[1][1]\)到\(A[1][3]\)，但我们又发现我们多删除了区间\(A[1][1]\)到\(A[1][2]\)，所以我们要加上它.
所以\(res=B[3][3]-B[3][2]-B[1][3]+B[1][2]\)。

来检验检验自己是否理解P1719最大加权矩形

有一个\(N\times N\)矩阵，要求矩阵中最大加权矩形，即矩阵的每一个元素都有一权值，权值定义在整数集上。从中找一矩形，矩形大小无限制，是其中包含的所有元素的和最大。矩阵的每个元素属于\([-127,127]\),\(N\leq 120\).

思路：计算出\(N\times N\)矩阵的前缀和，如果枚举找出一个矩形，这个矩形内包含的所有元素的和最大。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define endl '\n'
#define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
const int INF = 0x7fffffff;
const int N = 1e5+10;

int MAX = -INF;
int n, m, c, x, y, t, sum[130][130];
int main(){
	cin >> n;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			cin >> t;
			sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + t;
		}
	}
	 for(int x1 = 1; x1 <= n; x1++){
    	for(int y1 = 1; y1 <= n; y1++){
    		for(int x2 = 1; x2 <= n; x2++){
    			for(int y2 = 1; y2 <= n; y2++){
    				if(x2 < x1 || y2 < y1) continue;
    				MAX = max(MAX,sum[x2][y2] + sum[x1-1][y1-1] - sum[x2][y1-1] - sum[x1-1][y2]);
    			}
    		}
    	}
    }
	cout << MAX << endl;
	return 0;
}

二维差分

这里我们写的是前缀和和差分的对比理解，所以在这里我们使用的是二维差分的直接构造方法，

在一维差分中，我们曾说过这样一句话：数列\(A[]\)（原数组）是数列\(B[]\)（差分数组）的前缀和。同样的道理：在二维差分中，原数组也是差分数组的前缀和，使用我们通过前缀和的构造公式：\(b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j]\)（这里\(b[][]\)是前缀和数组，\(A[][]\)是原数组），我们可以知道二维差分的构造公式为：\(b[i][j]=a[i][j]−a[i−1][j]−a[i][j−1]+a[i−1][j−1]\)（这里\(b[][]\)是差分数组，\(A[][]\)是原数组）。

构造：

for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cin >> arr[i][j];
			b[i][j] = arr[i][j] - arr[i-1][j] - arr[i][j-1] + arr[i-1][j-1];
		}
	}

下面我们先把修改操作的代码给大家

for(int i = 1; i <= q; i++){
		cin >> x2 >> y2 >> x3 >> y3 >> c;
		b[x2][y2] += c;
		b[x2][y3+1] -= c;
		b[x3+1][y2] -= c;
		b[x3+1][y3+1] += c;
	}

每次对\(b\)数组执行以上操作，等价于

for(int i = x2; i <= x3; i++){
	for(int j = y2; j <= y3; j++){
        arr[i][j] += c;
    }
}

下面我们画图来理解这个修改过程：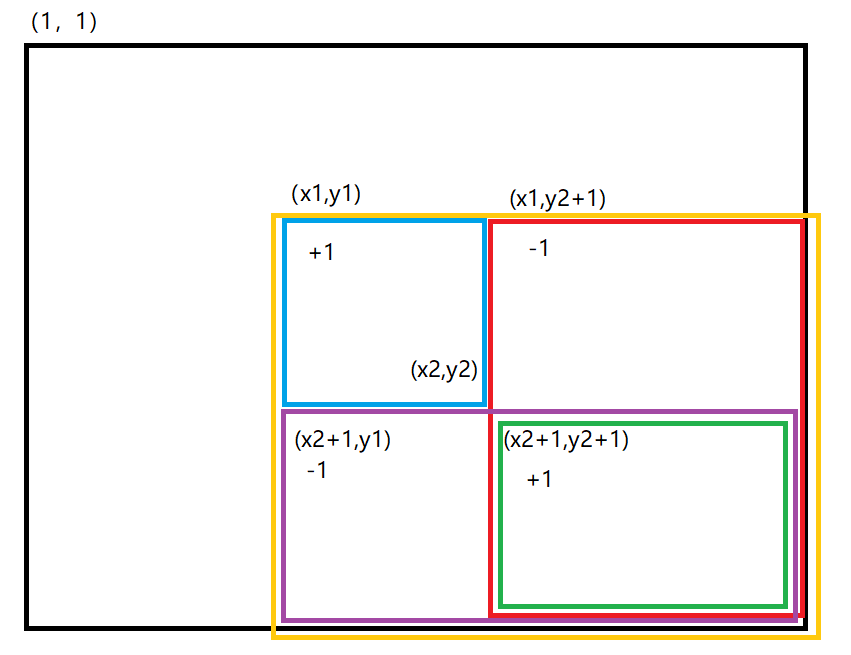
前缀和&差分_数组

\(b[x_1][y_1] += c\)；让整个\(arr\)数组中的黄色矩形内的每个元素都加上\(c\)；
\(b[x_1][y_2+1] -= c\)；让整个\(arr\)数组中的红色矩形内的每个元素都减去\(c\)，使其内元素不发生改变。
\(b[x_2+1][y_1] -= c\)；让整个\(arr\)数组中的紫色矩形内的每个元素都减去\(c\)，使其内元素不发生改变。
\(b[x_2+1][y_2+1] += c\)；让整个\(arr\)数组中的绿色矩形内的每个元素都加上\(c\)，绿色内的元素相当于减去了两次，所以我们要再加上一次，使其内的元素保持不变。
这就是整个二维差分的修改操作，最后我们只需要再求一次差分数组的前缀和，就可以得到被修改的原数组了。

最后我们看一道例题，来更好的理解二维差分798. 差分矩阵

输入一个\(n\)行\(m\)列的整数矩阵，再输入 \(q\)个操作，每个操作包含五个整数\(x_1,y_1,x_2,y_2,c\)，其中\((x_1,y_1)\)和\((x_2,y_2)\)表示一个子矩阵的左上角坐标和右下角坐标。每个操作都要将选中的子矩阵中的每个元素的值加上\(c\)。最后输出修改后的矩阵。\(1\leq n,m\leq 1000,1\leq q \leq 100000,1\leq x_1 \leq x_2\leq n,1\leq y_1\leq y_2\leq m,-1000\leq c\leq 1000,-1000\leq\)矩阵内元素的值\(\leq1000\)。

思路：这是一道二维差分的简单运用，我们可以先求出原数组的差分数组，在差分数组进行修改，最后在求差分数组的前缀和，即修改后的原数组。

#include <bits/stdc++.h>
#include <stack>
using namespace std;
typedef long long ll;
#define endl '\n'
const int INF = 0x3fffffff;
const int N = 1e6+10;

int n, m, q, x2, y2, x3, y3, c;
int arr[1010][1010], b[1010][1010];

int main(){
	cin >> n >> m >> q;
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cin >> arr[i][j];
            //求二维差分数组
			b[i][j] = arr[i][j] - arr[i-1][j] - arr[i][j-1] + arr[i-1][j-1];
		}
	}
	for(int i = 1; i <= q; i++){//修改二维差分数组
		cin >> x2 >> y2 >> x3 >> y3 >> c;
		b[x2][y2] += c;
		b[x2][y3+1] -= c;
		b[x3+1][y2] -= c;
		b[x3+1][y3+1] += c;
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
            //求修改后的原数组
			b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + b[i][j];
		}
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cout << b[i][j] << " ";
		}
		cout << endl;
	}
	return 0;
}

本文章为转载内容，我们尊重原作者对文章享有的著作权。如有内容错误或侵权问题，欢迎原作者联系我们进行内容更正或删除文章。