主成分分析（PCA）

理论介绍

PCA的全拼是Principal Component Analysis，翻译成中文就是主成分分析。在探索性数据分析中应用广泛，能更好地可视化在具有许多变量的数据集中出现的变化。这在“宽”数据集的情况下特别有用，在这种情况下，每个样本有许多变量。主成分分析的目的是在于降维，其结果是把多个指标归约为少数的几个指标，这少数的几个指标的表现形式一般为原来指标体系中的某几个指标线性组合。

个人认为，主成分分析就是通过降维来预测和寻找关键因子。

那什么情况下可以用主成分分析呢？话说这个真没有一个统一的标准，但一般认为数据需符合以下三条：

  1. 因子较多。
  2. 因子之间的共线性或相关性较强，所以要进行KMO检验。1
  3. 变量类型必须为连续变量，分类变量不可以。

下面说说主成分的原理，由于本人数学基础一般，所以这里仅简单总结一下。说白了，就是旋转坐标轴，来看个例子。

假如有两个变量是相关的，其散点图如下：

R语言中pch R语言中pca和mnn的区别_数据可视化


看看下面这个动图，是不很形象？黑线在旋转，红线和红点在变化。这就是PCA的工作过程，它在寻找最佳的黑线。标准是这条线上的差异应该最大化，也就是红点的分布越分散越好（方差）；另外误差最小化，这个好理解，就是蓝点到黑线的距离越小越好（投影）。PCA自动为我们找到了，根据勾股定理，嗯，大家都懂…

R语言中pch R语言中pca和mnn的区别_机器学习_02


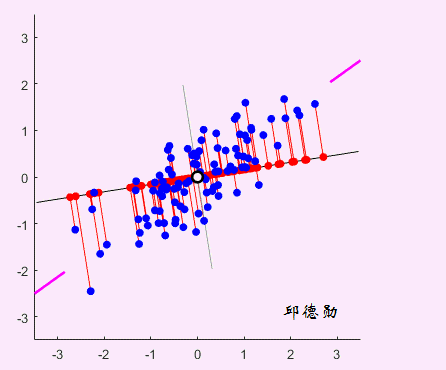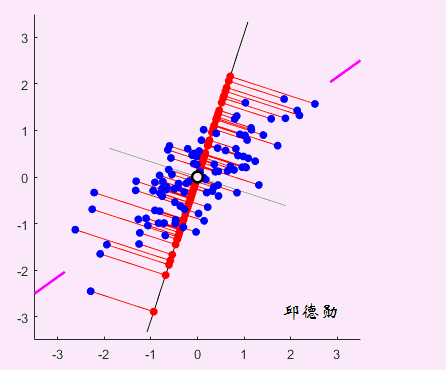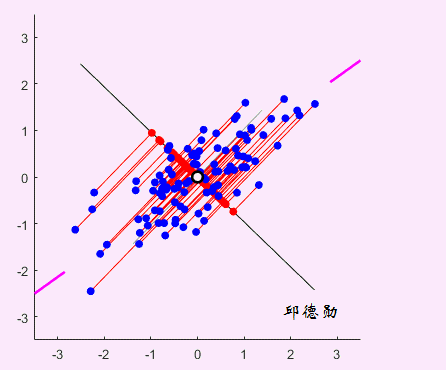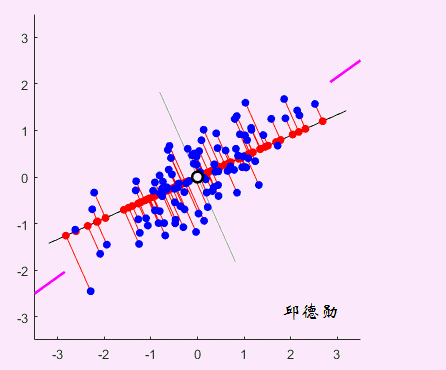
这是二维的数据，我们可以看出来数据变异最大的新维度，但是如果是更高维的就难以直观的呈现出来了。PCA有它的秘密武器，就是特征向量和特征值。一个是方向一个是长度，而在PCA中，有最大特征值的特征向量就是我们要找的主成分。引用别人的一句话：

特征向量定义了新的坐标系，它将原始数据转换到相互独立的两个方向上，且在主成分上方差达到最大化。

至于是怎么做到的呢，用协方差矩阵。这个就涉及到具体的数学推演了，作为非数理统计专业的，我不太会推，应用才是重点。

用R语言做PCA

说了半天，还没跟R语言扯上半毛钱关系。马上就来实战！
举个栗子，这里用到的是R自带的mtcars数据集。先来看看数据结构：

> str(mtcars)
'data.frame':	32 obs. of  11 variables:
 $ mpg : num  21 21 22.8 21.4 18.7 18.1 14.3 24.4 22.8 19.2 ...
 $ cyl : num  6 6 4 6 8 6 8 4 4 6 ...
 $ disp: num  160 160 108 258 360 ...
 $ hp  : num  110 110 93 110 175 105 245 62 95 123 ...
 $ drat: num  3.9 3.9 3.85 3.08 3.15 2.76 3.21 3.69 3.92 3.92 ...
 $ wt  : num  2.62 2.88 2.32 3.21 3.44 ...
 $ qsec: num  16.5 17 18.6 19.4 17 ...
 $ vs  : num  0 0 1 1 0 1 0 1 1 1 ...
 $ am  : num  1 1 1 0 0 0 0 0 0 0 ...
 $ gear: num  4 4 4 3 3 3 3 4 4 4 ...
 $ carb: num  4 4 1 1 2 1 4 2 2 4 ...

可以看到有11个变量，要注意的是vs和am是类别变量，而PCA分析只能是连续变量，所以要排除这两个变量。

> mtcars.pca <- prcomp(mtcars[,c(1:7,10,11)], center = TRUE,scale. = TRUE)
> summary(mtcars.pca)
Importance of components:
                          PC1    PC2     PC3     PC4     PC5     PC6     PC7    PC8     PC9
Standard deviation     2.3782 1.4429 0.71008 0.51481 0.42797 0.35184 0.32413 0.2419 0.14896
Proportion of Variance 0.6284 0.2313 0.05602 0.02945 0.02035 0.01375 0.01167 0.0065 0.00247
Cumulative Proportion  0.6284 0.8598 0.91581 0.94525 0.96560 0.97936 0.99103 0.9975 1.00000

9个变量得到PC1-9，看第二行Proportion of Variance，PC1解释了总方差的63％，PC2解释了23％，二者相加86%（累计贡献率），因此，前两个就是我们要找的主成分。
再来看看mtcars.pca的数据结构：

> str(mtcars.pca)
List of 5
 $ sdev    : num [1:9] 2.378 1.443 0.71 0.515 0.428 ...
 $ rotation: num [1:9, 1:9] -0.393 0.403 0.397 0.367 -0.312 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:9] "mpg" "cyl" "disp" "hp" ...
  .. ..$ : chr [1:9] "PC1" "PC2" "PC3" "PC4" ...
 $ center  : Named num [1:9] 20.09 6.19 230.72 146.69 3.6 ...
  ..- attr(*, "names")= chr [1:9] "mpg" "cyl" "disp" "hp" ...
 $ scale   : Named num [1:9] 6.027 1.786 123.939 68.563 0.535 ...
  ..- attr(*, "names")= chr [1:9] "mpg" "cyl" "disp" "hp" ...
 $ x       : num [1:32, 1:9] -0.664 -0.637 -2.3 -0.215 1.587 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:32] "Mazda RX4" "Mazda RX4 Wag" "Datsun 710" "Hornet 4 Drive" ...
  .. ..$ : chr [1:9] "PC1" "PC2" "PC3" "PC4" ...
 - attr(*, "class")= chr "prcomp"

嗯，看看就好，没啥可说的。

绘制PCA

可以说，以上都是在为绘制PCA铺垫。这里需要用到ggbiplot包，没有的话需要下载，如果下载失败，请看我的上一篇博客。
R语言PCA主成分分析——从github安装ggbiplot包

library(ggbiplot)
ggbiplot(mtcars.pca)

R语言中pch R语言中pca和mnn的区别_机器学习_03


箭头代表原始变量，其中方向代表原始变量与主成分的相关性，长度代表原始数据对主成分的贡献度。（我也不确定这么理解对不对）

然而，我们并不知道哪个点对应于哪个样本（汽车），就不是很有用。补充一下，mtcars里有32种汽车，11个变量（去掉俩还剩9个）。

来把这些点变成汽车的名字：

ggbiplot(mtcars.pca, labels=rownames(mtcars))

R语言中pch R语言中pca和mnn的区别_数据分析_04


现在可以看到哪些汽车彼此相似。例如，玛莎拉蒂Bora，法拉利Dino和福特Pantera L都聚集在顶部。这是有道理的，因为所有这些都是跑车，都是我买不起的车。

但我不知道该怎么让点和汽车名字同时显示…

我们还可以把这些汽车分为三类，分别属于美国，日本和欧洲的汽车，画3个椭圆。

mtcars.country <- c(rep("Japan", 3), rep("US",4), rep("Europe", 7),rep("US",3), "Europe", rep("Japan", 3), rep("US",4), rep("Europe", 3), "US", rep("Europe", 3))

ggbiplot(mtcars.pca,ellipse=TRUE, labels=rownames(mtcars), groups=mtcars.country)

rep(x, y)，x循环y次。栗子：
rep(1:2, 2)
1 2 1 2

R语言中pch R语言中pca和mnn的区别_r语言_05


可以看到，美国汽车在右边形成了一个独特的集群。美国车与cyl，disp和wt相关性大。日本汽车于mpg相关性大。欧洲汽车处于中间位置，并且不如任何一组更紧密地聚集。

让我们看一下PC3和PC4：

ggbiplot(mtcars.pca,ellipse=TRUE,choices=c(3,4), labels=rownames(mtcars),groups=mtcars.country)

R语言中pch R语言中pca和mnn的区别_R语言中pch_06


规律性不如PC1和PC2，因为PC3和PC4解释了总变化的很小的百分比。

有时候我们需要在图的中间画个圆：

ggbiplot(mtcars.pca,ellipse=TRUE,circle=TRUE, labels=rownames(mtcars), groups=mtcars.country)

R语言中pch R语言中pca和mnn的区别_r语言_07

ggbiplot(mtcars.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,  labels=rownames(mtcars), groups=mtcars.country)

R语言中pch R语言中pca和mnn的区别_r语言_08

ggbiplot(mtcars.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,var.axes=FALSE,   labels=rownames(mtcars), groups=mtcars.country)

R语言中pch R语言中pca和mnn的区别_r语言_09


由于ggbiplot是基于ggplot功能，可以使用同一组图形参数来改变图

。比如：

ggbiplot(mtcars.pca,ellipse=TRUE,obs.scale = 1, var.scale = 1,  labels=rownames(mtcars), groups=mtcars.country) +
  scale_colour_manual(name="Origin", values= c("forest green", "red3", "dark blue"))+
  ggtitle("PCA of mtcars dataset")+
  theme_minimal()+
  theme(legend.position = "bottom")

R语言中pch R语言中pca和mnn的区别_r语言_10

ggbiplot参数

?ggbiplot

ggbiplot(pcobj, choices = 1:2, scale = 1, pc.biplot =
  TRUE, obs.scale = 1 - scale, var.scale = scale, groups =
  NULL, ellipse = FALSE, ellipse.prob = 0.68, labels =
  NULL, labels.size = 3, alpha = 1, var.axes = TRUE, circle
  = FALSE, circle.prob = 0.69, varname.size = 3,
  varname.adjust = 1.5, varname.abbrev = FALSE, ...)

pcobj # prcomp()或princomp()返回结果
choices # 选择轴，默认1：2
scale   # covariance biplot (scale = 1), form biplot (scale = 0). When scale = 1, the inner product between the variables approximates the covariance and the distance between the points approximates the Mahalanobis distance.
obs.scale # scale factor to apply to observations
var.scale # scale factor to apply to variables
pc.biplot # 兼容 biplot.princomp()
groups # 组信息，并按组上色
ellipse # 添加组椭圆
ellipse.prob # 置信区间
labels  # 向量名称
labels.size # 名称大小
alpha # 点透明度 (0 = TRUEransparent, 1 = opaque)
circle # 绘制相关环(only applies when prcomp was called with scale = TRUE and when var.scale = 1)
var.axes # 为变量绘制箭头
varname.size # 变量名大小
varname.adjust # 标签与箭头距离 >= 1 表示远离箭头
varname.abbrev # 标签是否缩写

问题：为什么我运行ggbiplot中的例子失败？求解答

> wine.pca <- prcomp(wine, scale. = TRUE)
> print(ggbiplot(wine.pca, obs.scale = 1, var.scale = 1, groups = wine.class, ellipse = TRUE, circle = TRUE))
Error in ggbiplot(wine.pca, obs.scale = 1, var.scale = 1, groups = wine.class,  : 
  找不到对象'wine.class'

后记

主成分分析本身往往并不是目的，而是达到目的的一种手段。因此，它多用在大型研究项目的某个中间环节。例如，把它用在多重回归中，便产生了主成分回归。另外，它还可以用于聚类、判别分析等。比如，上面我们是手动赋予汽车的产地（美国，欧洲，日本），但如果是随机抽样，编号1-32，就可以先进行聚类分析，每一个椭圆代表一类。另外，分清PCA、PCoA、NMDS、CCA、RDA也很有必要。总之，数据分析需要花费大量的时间去学习和积累经验。我认为，最简单的方式就是读高质量的论文，把别人应用的方法借鉴过来。

坚持，厚积薄发！

  1. KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作因子分析；KMO值越接近于0，意味着变量间的相关性越弱，原有变量越不适合作因子分析。有人说KMO>0.7，才表示适合做主成分分析，仅供参考。 ↩︎