上一节说过,会单独写一节关于前面所有随机知识的梳理和总结。
这一节不可能会特别短,但很可能会有点长,因为以前的程序都写完了,这一节几乎没有新程序,而全部都是原理的详细分析(超级详细!详细到我觉得高中生都能看懂。)那好,就让我们做好心理准备,开始深入MC的世界。
目录:
一、MC与积分
二、球面积分再议
三、光散射公式
四、产生随机方向
五、结论:
一、MC与积分
首先还是我们要进行的积分:

结果就是下图中蓝色区域的面积:

其实也很好使用MC方法,产生一堆横坐标0-2,纵坐标0-4之间的随机数,然后判断其在蓝色区域还是黄色区域,然后根据比值计算出蓝色区域的值。但是这样有没有什么问题?肯定有:(这个问题我之前也阐述了好几段,现在再重新阐述一下)

如果是完全随机产生的均匀的随机数,那么从x轴上来说,产生在紫色部分的随机数,贡献率会比产生在粉色区域的贡献率大。这是为什么呢?
再把之前的话放上:这种求积分的方式,其实就是求整段线的均值,然后乘以横坐标长度,即这里为2。
比如,我要计算x^2从0到2的积分,我们真实地计算一下发现,从0到1积分起来的值只有1/3,而从1到2积分的值是7/3,所以说,从1-2的积分的值不就占比重更大吗?当我们要通过估计的方法来获得值的时候,假如我们随机产生200个数,其中100个在(0-1)之间,100个在(1-2)之间,假设通过100个数的估计偏差在2%左右,则从0-1积分的估计值与真实值的偏差是0.0067(即(1/3)*0.02),而从1-2积分值的估计值与真实值的偏差为 0.047(即(7/3)*0.02),两个偏差加起来的值是0.053左右。
如果我们进行一下分配,让随机数在1-2之间产生的更多,这样就会降低1-2之间积分的偏差。根据刚才的计算,我们知道1-2之间占积分值比重很大,所以这样就能很好的降低总的偏差。

还是这个图,如果我们能知道产生的每个随机点的权重,那么就可以很快地逼近了。
解释方法:上面的蓝色区域中,随便选其中一部分并计算面积,如果知道它的面积占总面积的比重,就能得到总的面积。
我们从图中可以看到,横坐标值越大,随机点出现在蓝色中的比例越大,这种比例关系是线性关系吗?不是。(我们只知道它呈现正相关,至于是不是线性正相关,废话,这是个曲线,肯定不是线性关系。如果学过微积分就知道其实是x的三次方的关系)。但是没有关系,在实际例子中我们一般都很难明确待求问题的pdf,但我们既然知道了呈正相关,就自己设计一个产生正相关随机数的产生器,然后再除以该随机数产生器的权重不就好了
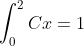
因为概率密度函数积分为1.
得到C = 0.5。
于是,在这个随机数发生器的帮助下,我们得到了大量的随机数rs,这些随机数分布符合p(x)=0.5x,每个随机数 r 的值为 r^2。注意这里的p(x)是其占比,即重要性,若p(r)大的话,表示我们产生的随机数,在 r 这里的可能性更大。但是如果大量的数都产生在x更大的地方的话,会对最后的积分值有影响,所以需要除以其比重:r^2/p(r),即 f(x)/p(x) , f(x) = x^2。所以要求出f(x)的平均值,就是计算出 (f(x1)/p(x1)+f(x2)/p(x2)+f(x3)/p(x3)+f(x4)/p(x4)+......+f(xN)/p(xN))/N 。
那么现在的问题是怎么产生pdf为p(x)=0.5x的随机数——但是以前的章节已经讲的已经很明白了,这里就跳过。
(p.s.说句题外话。概率论真的是一门有趣和神奇的学科,以前大学里学习过好几遍概率论与数理统计,但是现在每次再学习还是会有所收获。概率论薄弱的同学可以先学习一下MIT的概率论与数理统计课程,然后再学习一些关于随机过程方面的知识(例如孙应飞老师的随机过程),加深一下应用和理解。)
现在我们为了加深一下理解,来使用绝对均匀的随机数:p(x) =C
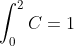
,C=0.5
所以我们的公式就变为了 (2*f(x1)+2*f(x2)+2*f(x3)+2*f(x4)+......+2*f(xN))/N (注意xN是产生在0-2上的随机数)
注意,这里的2和前面2*sum/N中的2看着一样,但其实不同,这里的2是每个随机数的pdf处理的
我们再来设计一个pdf: p(x)=Cx^2
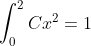
, C=8/3
P(x) = 1/8x^3 反函数 y=(8x)^1/3
x*x / pdf(x) = (x*x) / (3/8x*x) = 8/3,所以一次就能得到正确的值。但当然一般情况下我们不知道被积函数自变量x的分布,所以这种完美解决的情况并不多见。
本节最难理解的一点是:
为什么 sum += x*x / pdf(x);
sum / N 的结果为蓝色区域的面积,而不是f(x)的平均值(即面积除以横坐标长度2)。
前面已经分析过多次,现在再添加一种理解方式:因为pdf积分从0到2后一定是1,所以我们以均匀随机数为例,一半产生在0-1之间,一半产生在1-2之间。如果要计算x^2从0到1之间的积分的话,pdf=1,而且 sum / N 的结果既是f(x)平均值,也是f(x)积分的面积。当积分区间增大一倍以后,因为pdf积分为1,所以pdf缩小一倍,变为了0.5,但仍然是随机均匀分布的。这个时候,sum/N 的结果就应该是面积了。
二、球面积分再议
计算积分:
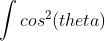
其中 theta 是与Z轴的夹角。因为是一整个球面,而不是半球,所以产生的向量全都均匀随机分布在表面。
对一个单位球面进行积分,得到单位球面的面积4Pi,而因为这里的pdf是常数,所以对一个常数在单位球面积分,等于积分后乘该常数,所以随机向量在每个方向的权重都是球体的表面积的倒数,即1/(4*Pi)。
所以对cos^2(theta)积分就是
(cos^2(theta1)/(1/(4*Pi))+cos^2(theta2)/(1/(4*Pi))+cos^2(theta3)/(1/(4*Pi))+cos^2(theta4)/(1/(4*Pi))+
......+cos^2(thetaN)/(1/(4*Pi)))/N
注意对于产生的单位随机向量r,cos(theta_r) = (0,0,1)·(r.x(),r.y(),r.z())=r.z()
所以积分就变为了:
(r1.z()*r1.z()/(1/(4*Pi))+r2.z()*r2.z()/(1/(4*Pi))+r3.z()*r3.z()/(1/(4*Pi))+r4.z()*r4.z()/(1/(4*Pi))+
......+rN.z()*rN.z()/(1/(4*Pi)))/N我们要注意,这里的积分并不是简单地把从
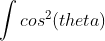
0积分到Pi,而是:

即:
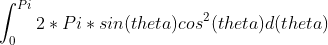
而不是

注意这里的2*Pi*sin(theta)的意义会在下面第四节来详细讲(其实抛去cos^2(theta)后的积分结果就是球的表面积)。
三、光散射公式
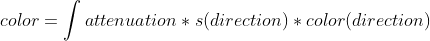
根据前面所述的理论,采用重要性抽样后:
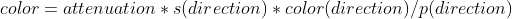
前面我说的比较简略,这里我再重新强调一下,这里比前面的积分中多了一个s(direction),这是散射方向direction的分布pdf,也就是说散射光在哪个方向分布的多以及哪个方向分布的少。我们对不同方向的s(direction)color(direction)积分,就得到的是全部方向上的信息,也就是全局光照(从各个方向都考虑到了)
第一种:散射pdf=采样pdf
s(direction)=p(direction),即
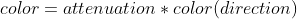
,即散射的pdf等同于采样方向的pdf。
第二种:(常规情况)
散射pdf≠采样方向的pdf。注意这个散射方向的pdf是我们自己定义的,根据物理分析,lambertian材料的散射pdf分布就是我们之前用的这个 cos(theta)/Pi
为什么要设置不一样呢?有的人可能觉得,按照lambertian材料散射的pdf计算不是更方便吗?不是这样的。因为我们要知道,采样的时候,如果最终采样不到灯光,就是黑点,对最后的结果不做任何贡献,所以根据重要性采样原理,要尽可能超光源的方位散射,即s(direction)≠p(direction)。
第一种的结果:

第二种,设置散射光线pdf为1/(2*Pi),即在半球上随机分布:

四、产生随机方向
我们产生的随机坐标(x,y,z)真的是在方向上随机吗?真的是在方向上密度均匀吗?是的。
但是现在,要求变了:我们想生成符合一定规律的向量,例如,在法线附近生成几率比较大,所以要通过一些方法来进行约束。
还记得我们这一节的程序吗?就是生成两个随机数,然后用这两个随机数生成向量。为什么两个就够了,很简单,因为我们要生成的向量是关于Z轴旋转对称的,所以只需要两个变量就够了。要生成朝向 (θ,phi) 的单位矢量方向,根据球面坐标公式:
x = cos(phi)*sin(theta)
y = sin(phi)*sin(theta)
z = cos(theta)所以要生成一个随机的theta和一个随机的phi,但是,如何根据限制theta和phi的pdf来约束生成的随机向量呢?(核心问题)
生成向量的pdf关于Z轴旋转对称的,所以phi的pdf: a(phi) = 1/(2Pi) (是uniform的)

图中紫色圆的紫色线段代表 sin(theta),2*Pi*sin(theta)就是圆的周长,对其进行积分就是圆的表面积,所以:
b(theta) = 2*Pi*f(theta)sin(theta)
pdf的积分一定为1,积分即P(表示概率)。
所以生成两个[0-1]之间的随机数作为概率P,然后令:
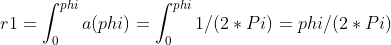
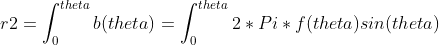
根据 f(theta) 的不同,可以生成不同 pdf 的随机向量。
如果要在上半球积分:
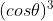
,即:
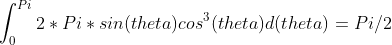
使用均匀分布pdf p(directions)=1/(2*Pi),所以我们的均值为

对应书本上的程序:

使用非均匀分布pdf p(directions) = cos(theta) / Pi,所以我们的均值为
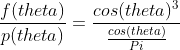
对应书本上的程序:

五、结论:
终于写完这一节了,花了整整一天的时间,自认为这一节已经讲述的非常明白和确切了。结合前面的五节课程,奠定了一个很坚实的基础!MC估计积分值,就是将采样值除以该采样的概率,把多次采样值取平均,就会逼近真实的积分值。





















