本节书摘来华章计算机出版社《R的极客理想——高级开发篇 A》一书中的第1章,第1.4节,作者:张丹
1.4 常用连续型分布介绍及R语言实现
问题
如何让R语言画出概率分布函数曲线?

引言
随机变量在我们的生活中处处可见,如每日天气、股价涨跌、彩票中奖等,这些事情都是事前不可预言其结果的,就算在相同的条件下重复进行试验,其结果未必相同。数学家们总结了这种规律,用概率分布来描述随机变量取值。就算股价不能预测,但如果知道了它的波动率的概率分布,那么我们就会有更大的机会猜出答案。
本节将介绍用R语言画出多种连续型概率分布的曲线,包括正态分布、指数分布、伽玛分布、韦布尔分布、F分布、T分布、贝塔分布、卡方分布、均匀分布。
1.4.1 均匀分布
本节的系统环境是:
Windows 7 64bit
R: 3.1.1 x86_64-w64-mingw32/x64 (64-bit)
均匀分布(uniform distribution)是均匀的、不偏差的一种简单的概率分布,分为离散型均匀分布与连续型均匀分布,本节只介绍连续型的概率分布部分。
1.?概率密度函数
均匀分布的概率密度函数由式(1.13)给出。

(1.13)下面的R程序画出均匀分布的概率密度函数曲线:
set.seed(1) # 设置随机种子
x<-seq(0,10,length.out=1000) # 取从0~10顺序取的1000个点
y<-dunif(x,0,1) # 计算服从均匀分布U(0,1),1000个点的概率密度函数的值plot(x,y,col="red",xlim=c(0,10),ylim=c(0,1.2),type='l',xaxs="i", yaxs="i",
ylab='density',xlab='',main="The Uniform Density Distribution") # 画出概率密度函数曲线,如图1-12所示
lines(x,dnorm(x,0,0.5),col="green") # 计算服从均匀分布U(0,0.5)的值,并增加一条曲线
lines(x,dnorm(x,0,2),col="blue") # 计算服从均匀分布U(0,2)的值,并增加一条曲线
lines(x,dnorm(x,-2,1),col="orange") # 计算服从均匀分布U(-2,1)的值,并增加一条曲线
lines(x,dnorm(x,4,2),col="purple") # 计算服从均匀分布U(4,2)的值,并增加一条曲线
legend("topright",legend=paste("m=",c(0,0,0,-2,4)," sd=", c(1,0.5,2,1,2)),lwd=1, col=c("red", "green","blue","orange","purple")) # 在右上角增加图例

2.?累积分布函数
均匀分布的累积分布函数公式为(1.14):

下面的R程序画出均匀分布的累积分布函数曲线:
set.seed(1) # 设置随机种子
x<-seq(0,10,length.out=1000) # 取从0~10顺序取的1000个点
y<-punif(x,0,1) # 计算服从均匀分布U(0,1),1000个点的累积分布函数的值plot(x,y,col="red",xlim=c(0,10),ylim=c(0,1.2),type='l',xaxs="i", yaxs="i",
> lines(x,punif(x,0,0.5),col="green")
> lines(x,punif(x,0,2),col="blue")
> lines(x,punif(x,-2,1),col="orange")
> legend("bottomright",legend=paste("m=",c(0,0,0,-2)," sd=", c(1,0.5,2,1)),
lwd=1, col=c("red", "green","blue","orange","purple"))3.?分布检验
Kolmogorov-Smirnov连续分布检验是检验单一样本是不是服从某一预先假设的特定分布的方法。把样本数据的累计频数分布与特定理论分布相比较,若两者间的差距很小,则推论该样本取自某特定分布族。
均匀分布检验的原假设为H0:数据集符合均匀分布,备择假设为H1:样本所来自的总体分布不符合均匀分布。令F0(x)表示预先假设的理论分布,Fn(x)表示随机样本的累计概率(频率)函数。统计量D为:
D=max|F0(x)-Fn(x)|
D值越小,越接近0,表示样本数据越接近均匀分布
p值,如果p值小于显著性水平α(0.05),则拒绝H0
set.seed(1) # 设置随机种子
S<-runif(1000) # 生成服从均匀分布的1000点
ks.test(S, "punif") # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0244, p-value = 0.5928
alternative hypothesis: two-sided
D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合均匀分布!
后文中其他函数的分布检验也使用的是Kolmogorov-Smirnov的检验方法,因此后面检验描述从略。
1.4.2 正态分布
正态分布(normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个位置参数为μ、尺度参数为σ2的高斯分布,则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记为N(μ, σ2)。数学期望μ决定了分布位置,标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ=0, σ=1的正态分布。
1.?概率密度函数
正态分布的概率密度函数公式为(1.15):
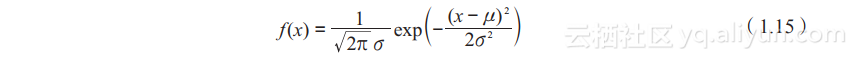(1.15)
下面的R程序画出正态分布的概率密度函数曲线:
set.seed(1)
x <- seq(-5,5,length.out=100) # 取从-5到5的100个点
y <- dnorm(x,0,1) # 计算服从正态分布N(0,1),100个点的概率密度函数的值plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab
='density',xlab='',main="The Normal Density Distribution") # 画出概率密度函数曲线,如图1-14所示
lines(x,dnorm(x,0,0.5),col="green")
lines(x,dnorm(x,0,2),col="blue")
lines(x,dnorm(x,-2,1),col="orange")
legend("topright",legend=paste("m=",c(0,0,0,-2)," sd=", c(1,0.5,2,1)), lwd=1,col=c("red", "green","blue","orange"))

2.?累积分布函数
正态分布的概率密度函数公式为(1.16):

下面的R程序画出正态分布的累积分布函数曲线:
set.seed(1)
x <- seq(-5,5,length.out=100)
y <- pnorm(x,0,1) # 计算服从正态分布N(0,1),100个点的累积分布函数的值
> plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,1),type='l',xaxs="i", yaxs="i",
ylab='F(x)',xlab='',main="The Normal Cumulative Distribution")
# 画出累积分布函数曲线,如图1-15所示
> lines(x,pnorm(x,0,0.5),col="green")
> lines(x,pnorm(x,0,2),col="blue")
> lines(x,pnorm(x,-2,1),col="orange")
> legend("bottomright",legend=paste("m=",c(0,0,0,-2)," sd=", c(1,0.5,2,1)),
lwd=1,col=c("red", "green","blue","orange"))3.?分布检验
Shapiro-Wilk正态分布检验用来检验数据是否符合正态分布,同线性回归的方法一样,是检验其与回归曲线的残差。该方法推荐在样本量很小的时候使用,一般是样本在3~5000之间。
Shapiro-Wilk正态分布检验的原假设为H0:数据集符合正态分布,统计量W为

(1.17)其中统计量W最大值是1,越接近1,表示样本与正态分布越匹配。如果p值小于显著性水平α(0.05),则拒绝H0
set.seed(1)
S<-rnorm(1000) # 生成服从正态分布的1000点
shapiro.test(S) # Shapiro-Wilk正态分布检验Shapiro-Wilk normality test
data: S
W = 0.9988, p-value = 0.7256
这里W接近1,p值>0.05,不能拒绝原假设,所以数据集S符合正态分布!
若用Kolmogorov-Smirnov连续分布检验,原假设为H0:数据集符合正态分布,备择假设为H1:样本所来自的总体分布不符合正态分布。
set.seed(1)
S<-rnorm(1000)
ks.test(S, "pnorm") # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0211, p-value = 0.7673
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合正态分布!
1.4.3 指数分布
指数分布(exponential distribution)用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等。许多电子产品的寿命一般服从指数分布,有的系统的寿命分布也可用指数分布来近似。当产品的失效是偶然失效时,其寿命服从指数分布。指数分布的失效率是与时间t无关的常数,所以分布函数简单。指数分布在可靠性研究中是最常用的一种分布形式。
1.?概率密度函数
指数分布的概率密度函数公式为(1.18):
(1.18)
其中λ>0是分布的参数,常被称为率参数(rate parameter),即每单位时间发生该事件的次数。指数分布的取值区间是[0,∞)。如果一个随机变量X呈指数分布,则可以写作X~Exponential(λ)。
下面的R程序画出指数分布的概率密度函数曲线。
set.seed(1)
x<-seq(-1,2,length.out=100)
y<-dexp(x,0.5) # 计算服从指数分布e(0.5),100个点的概率密度函数的值plot(x,y,col="red",xlim=c(0,2),ylim=c(0,5),type='l',xaxs="i", yaxs="i",ylab=
'density',xlab='',main="The Exponential Density Distribution") # 画出概率密度函数曲线,如图1-16所示
lines(x,dexp(x,1),col="green")
lines(x,dexp(x,2),col="blue")
lines(x,dexp(x,5),col="orange")
legend("topright",legend=paste("rate=",c(.5, 1, 2,5)), lwd=1,col=c("red","green","blue","orange"))

2.?累积分布函数
指数分布的累积分布函数公式为(1.19):

下面的R程序画出指数分布的累积分布函数曲线。
set.seed(1)
x<-seq(-1,2,length.out=100)
y<-pexp(x,0.5) # 计算服从指数分布e(0.5),100个点的累积分布函数的值plot(x,y,col="red",xlim=c(0,2),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab=
'F(x)',xlab='',main="The Exponential Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-17所示
lines(x,pexp(x,1),col="green")
lines(x,pexp(x,2),col="blue")
lines(x,pexp(x,5),col="orange")
legend("bottomright",legend=paste("rate=",c(.5, 1, 2,5)), lwd=1, col=c("red","green","blue","orange"))
3.?分布检验
对指数分布来说,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合指数分布,备择假设为H1:样本所来自的总体分布不符合指数分布。
set.seed(1)
S<-rexp(1000)
ks.test(S, "pexp") # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0387, p-value = 0.1001
alternative hypothesis: two-sided
这里,D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合指数分布!
1.4.4 伽玛分布
伽玛分布(Gamma)是著名的皮尔逊概率分布函数簇中重要的一员,称为皮尔逊Ⅲ型分布。它的曲线有一个峰,但左右不对称。伽玛函数是阶乘在实数上的泛化,其公式为(1.20):
(1.20)
1.?概率密度函数
伽玛分布的概率密度函数公式为(1.21):

(1.21)其中k为形状参数,θ为尺度参数。
下面的R程序画出伽玛分布的概率密度函数曲线。
set.seed(1)
x<-seq(0,10,length.out=100)
y<-dgamma(x,1,2) # 计算服从伽玛分布Ga(1,2),100个点的概率密度函数的值plot(x,y,col="red",xlim=c(0,10),ylim=c(0,2),type='l',xaxs="i", yaxs="i",ylab=
'density',xlab='',main="The Gamma Density Distribution") # 画出概率密度函数曲线,如图1-18所示
lines(x,dgamma(x,2,2),col="green")
lines(x,dgamma(x,3,2),col="blue")
lines(x,dgamma(x,5,1),col="orange")
lines(x,dgamma(x,9,1),col="black")
legend("topright",legend=paste("shape=",c(1,2,3,5,9)," rate=", c(2,2,2,1,1)),lwd=1, col=c("red", "green","blue","orange","black"))
2.?累积分布函数
伽玛分布的累积分布函数公式为(1.22):

(1.22)下面的R程序画出伽玛分布的累积分布函数曲线。
set.seed(1)
x<-seq(0,10,length.out=100)
y<-pgamma(x,1,2) # 计算服从伽玛分布Ga(1,2),100个点的累积分布函数的值plot(x,y,col="red",xlim=c(0,10),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab=
'F(x)',xlab='',main="The Gamma Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-19所示
lines(x,pgamma(x,2,2),col="green")
lines(x,pgamma(x,3,2),col="blue")
lines(x,pgamma(x,5,1),col="orange")
lines(x,pgamma(x,9,1),col="black")
legend("bottomright",legend=paste("shape=",c(1,2,3,5,9)," rate=",c(2,2,2,1,1)), lwd=1, col=c("red", "green","blue","orange","black"))

3.?分布检验
对伽玛分布来说,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合伽玛分布,备择假设为H1:样本所来自的总体分布不符合伽玛分布。
set.seed(1)
S<-rgamma(1000,1)
ks.test(S, "pgamma", 1) # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0363, p-value = 0.1438
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合形状参数为1伽玛分布!
下面我们做一个检验失败的测试,如果设检验形状参数为2,那么用Kolmogorov-Smirnov检验时,结果就不是符合我们预期的。
ks.test(S, "pgamma", 2) # Kolmogorov-Smirnov检验
One-sample Kolmogorov-Smirnov test
data: S
D = 0.3801, p-value < 2.2e-16
alternative hypothesis: two-sided
这里D值不够小,p值<0.05,拒绝原假设,所以数据集S不符合形状参数为2伽玛分布!
1.4.5 韦布尔分布
韦布尔(Weibul)分布,又称韦氏分布或韦伯分布,是可靠性分析和寿命检验的理论基础。韦布尔分布由形状、尺度(范围)和位置三个参数决定,其中形状参数是最重要的参数,决定分布密度曲线的基本形状,尺度参数起放大或缩小曲线的作用,但不影响分布的形状。
韦布尔分布通常用在故障分析领域中;尤其是它可以模拟故障率(failture rate)持续变化的分布。如果故障率:
一直为常量(constant over time),那么α=1,暗示在随机事件中发生;
一直减少(decreases over time),那么α<1,暗示“早期失效(infant mortality)”;
一直增加(increases over time),那么α>1,暗示“耗尽(wear out)”,即随着时间的推进,失败的可能性变大。
1.?概率密度函数
韦布尔分布的概率密度函数公式为(1.23):

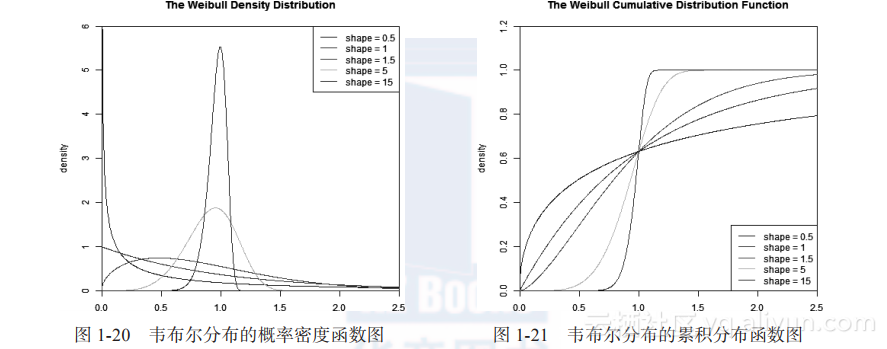
(1.23)下面的R程序画出韦布尔分布的概率密度函数曲线。
set.seed(1)
x<- seq(0, 2.5, length.out=1000)
y<- dweibull(x, 0.5) # 计算服从韦布尔分布W(0.5,1),1000个点的概率密度函数的值plot(x, y, type="l", col="blue",xlim=c(0, 2.5),ylim=c(0, 6),xaxs="i", yaxs=
"i",ylab='density',xlab='',main="The Weibull Density Distribution") # 画出概率密度函数曲线,如图1-20所示
lines(x, dweibull(x, 1), type="l", col="red")
lines(x, dweibull(x, 1.5), type="l", col="magenta")
lines(x, dweibull(x, 5), type="l", col="green")
lines(x, dweibull(x, 15), type="l", col="purple")
legend("topright", legend=paste("shape =", c(.5, 1, 1.5, 5, 15)),lwd=1,col=c("blue", "red", "magenta", "green","purple"))
2.?累积分布函数
韦布尔分布的累积分布函数公式为(1.24):
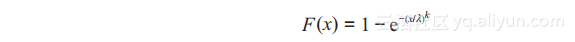(1.24)
下面的R程序画出韦布尔分布的累积分布函数曲线。
set.seed(1)
x<- seq(0, 2.5, length.out=1000)
y<- pweibull(x, 0.5) # 计算服从weibull分布W(0.5,1),1000个点的累积分布函数的值plot(x, y, type="l", col="blue",xlim=c(0, 2.5),ylim=c(0, 1.2),xaxs="i", yaxs=
"i",ylab='F(x)',xlab='',main="The Weibull Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-21所示
lines(x, pweibull(x, 1), type="l", col="red")
lines(x, pweibull(x, 1.5), type="l", col="magenta")
lines(x, pweibull(x, 5), type="l", col="green")
lines(x, pweibull(x, 15), type="l", col="purple")
legend("bottomright", legend=paste("shape =", c(.5, 1, 1.5, 5, 15)), lwd=1,col=c("blue", "red", "magenta", "green","purple"))
图1-20 韦布尔分布的概率密度函数图 图1-21 韦布尔分布的累积分布函数图
3.?分布检验
对于韦布尔分布,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合韦布尔分布,备择假设为H1:样本所来自的总体分布不符合韦布尔分布。
set.seed(1)
S<-rweibull(1000,1)
ks.test(S, "pweibull",1) # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0244, p-value = 0.5928
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合形状参数为1的韦布尔分布!
1.4.6 卡方分布
若n个相互独立的随机变量ξ1, ξ2, …, ξn均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一个新的随机变量,其分布规律称为卡方(χ2, chi-square)分布。其中参数n称为自由度,自由度不同就是另一个卡方分布,正如正态分布中均值或方差不同就是另一个正态分布一样。
1.?概率密度函数
卡方分布的概率密度函数公式为(1.25):
(1.25)
其中分母Γ是伽玛函数。
下面是R程序画出卡方分布的概率密度函数曲线。
set.seed(1)
x<-seq(0,10,length.out=1000)
y<-dchisq(x,1) # 计算服从卡方分布X(1),1000个点的概率密度函数的值plot(x,y,col="red",xlim=c(0,5),ylim=c(0,2),type='l',xaxs="i", yaxs="i",ylab=
'density',xlab='',main="The Chisq Density Distribution") # 画出概率密度函数曲线,如图1-22所示
lines(x,dchisq(x,2),col="green")
lines(x,dchisq(x,3),col="blue")
lines(x,dchisq(x,10),col="orange")
legend("topright",legend=paste("df=",c(1,2,3,10)), lwd=1, col=c("red","green","blue","orange"))
2.?累积分布函数
卡方分布的累积分布函数公式为(1.26):

(1.26)其中分母Γ是伽玛函数,分子γ(k, z)为不完全伽玛函数。
下面的R程序画出卡方分布的累积分布函数曲线。
set.seed(1)
x<-seq(0,10,length.out=1000)
y<-pchisq(x,1) # 计算服从卡方分布X(1),1000个点的累积分布函数的值plot(x,y,col="red",xlim=c(0,10),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab=
'F(x)',xlab='',main="The Chisq Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-23所示
lines(x,pchisq(x,2),col="green")
lines(x,pchisq(x,3),col="blue")
lines(x,pchisq(x,10),col="orange")
legend("topleft",legend=paste("df=",c(1,2,3,10)), lwd=1, col=c("red", "green","blue","orange"))

3.?分布检验
对于卡方分布,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合卡方分布,备择假设为H1:样本所来自的总体分布不符合卡方分布。
set.seed(1)
S<-rchisq(1000,1)
ks.test(S, "pchisq",1) # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0254, p-value = 0.5385
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合自由度为1的卡方分布!
1.4.7 F分布
F分布是一种连续型概率分布,广泛应用于似然比率检验,特别是ANOVA中。F分布的定义为:设X,Y为两个独立的随机变量,X服从自由度为d1的卡方分布,Y服从自由度为d2的卡方分布,则 服从自由度为d1和d2的F分布。
F分布是一种非对称分布,它有两个自由度,即d1和d2,相应的分布记为F(d1, d2),d1通常称为分子自由度,d2通常称为分母自由度。F分布是一个以自由度d1和d2为参数的分布族,不同的自由度决定了F分布的形状。
1.?概率密度函数
F分布的概率密度函数公式为(1.27):
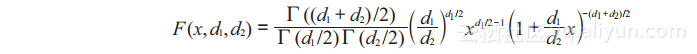(1.27)
其中Γ是伽玛函数。
下面的R程序画出F分布的概率密度函数曲线。
set.seed(1)
x<-seq(0,5,length.out=1000)
y<-df(x,1,1,0) # 计算服从F分布F(1,1,0),1000个点的概率密度函数的值plot(x,y,col="red",xlim=c(0,5),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab=
'density',xlab='',main="The F Density Distribution") # 画出概率密度函数曲线,如图1-24所示
lines(x,df(x,1,1,2),col="green")
lines(x,df(x,2,2,2),col="blue")
lines(x,df(x,2,4,4),col="orange")
legend("topright",legend=paste("df1=",c(1,1,2,2),"df2=",c(1,1,2,4)," ncp=",c(0,2,2,4)), lwd=1, col=c("red", "green","blue","orange"))
2.?累积分布函数
F分布的累积分布函数公式为(1.28):
(1.28)
其中I是不完全Beta函数
下面的R程序画出F分布的累积分布函数曲线。
set.seed(1)
x<-seq(0,5,length.out=1000)
y<-df(x,1,1,0) # 计算服从F分布F(1,1,0),1000个点的累积分布函数的值plot(x,y,col="red",xlim=c(0,5),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab=
'F(x)',xlab='',main="The F Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-25所示
lines(x,pf(x,1,1,2),col="green")
lines(x,pf(x,2,2,2),col="blue")
lines(x,pf(x,2,4,4),col="orange")
legend("topright",legend=paste("df1=",c(1,1,2,2),"df2=",c(1,1,2,4)," ncp=",c(0,2,2,4)), lwd=1, col=c("red", "green","blue","orange"))

3.?分布检验
对于F分布,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合F分布,备择假设为H1:样本所来自的总体分布不符合F分布。
set.seed(1)
S<-rf(1000,1,1,2)
ks.test(S, "pf", 1,1,2) # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0113, p-value = 0.9996
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合df1=1, df2=1, ncp=2的F分布!
1.4.8 t分布
学生t分布(Student’s t-Distribution),可简称为t分布,应用于估计呈正态分布的总体之平均数。它是对两个样本均值差异进行显著性测试的学生t检验的基础。学生t检验改进了Z检验(Z-test),因为Z检验以总体标准差已知为前提。虽然在样本数量大(超过30个)时,可以应用Z检验来求得近似值,但Z检验用在小样本会产生很大的误差,因此必须改用学生t检验以求准确。
1.?概率密度函数
t分布的概率密度函数公式为

(1.29)其中等于n-1,一般称为自由度;Γ是伽玛函数。
下面的R程序画出t分布的概率密度函数曲线。
set.seed(1)
x<-seq(-5,5,length.out=1000)
y<-dt(x,1,0) # 计算服从t分布T(1,0),1000个点的概率密度函数的值plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,0.5),type='l',xaxs="i", yaxs="i",ylab
='density',xlab='',main="The T Density Distribution") # 画出概率密度函数曲线,如图1-26所示
lines(x,dt(x,5,0),col="green")
lines(x,dt(x,5,2),col="blue")
lines(x,dt(x,50,4),col="orange")
legend("topleft",legend=paste("df=",c(1,5,5,50)," ncp=", c(0,0,2,4)), lwd=1,col=c("red", "green","blue","orange"))
2.?累积分布函数
t分布的累积分布函数公式为(1.30):
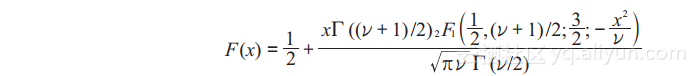(1.30)
其中等于n-1,一般称为自由度;Γ是伽玛函数。
下面的R程序画出t分布的累积分布函数曲线。
set.seed(1)
x<-seq(-5,5,length.out=1000)
y<-pt(x,1,0) # 计算服从T分布T(1,0),1000个点的累积分布函数的值plot(x,y,col="red",xlim=c(-5,5),ylim=c(0,0.5),type='l',xaxs="i", yaxs="i",ylab
='F(x)',xlab='',main="The T Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-27所示
lines(x,pt(x,5,0),col="green")
lines(x,pt(x,5,2),col="blue")
lines(x,pt(x,50,4),col="orange")
legend("topleft",legend=paste("df=",c(1,5,5,50)," ncp=", c(0,0,2,4)), lwd=1,col=c("red", "green","blue","orange"))
3.?分布检验
对于t分布,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合t分布,备择假设为H1:样本所来自的总体分布不符合t分布。
set.seed(1)
S<-rt(1000, 1,2)
ks.test(S, "pt", 1, 2) # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0253, p-value = 0.5461
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合df=1, ncp=2的t分布!
1.4.9 贝塔分布
贝塔(Beta)分布是指一组定义在(0, 1)区间的连续概率分布,Beta分布有α和β两个参数,α, β>0,其中α为成功次数加1,β为失败次数加1。
贝塔分布通常用来为取值于某有限区间[c, d]的随机现象建立模型。当然,如果令c为原点,而d-c为单位长度,那么可将取值区间转化为[0, 1]。贝塔分布的一个重要应用是作为伯努利分布和二项式分布的共轭先验分布出现,在机器学习和数理统计学中有重要应用。
1.?概率密度函数
概率密度函数公式为(1.31):

(1.31)
其中随机变量X服从参数为, β的贝塔分布,Γ是伽玛函数
下面的R程序画出贝塔分布的概率密度函数曲线。
set.seed(1)
x<-seq(-5,5,length.out=10000)
y<-dbeta(x,0.5,0.5) # 计算服从贝塔分布B(0.5,0.5),10000个点的概率密度函数的值plot(x,y,col="red",xlim=c(0,1),ylim=c(0,6),type='l',xaxs="i", yaxs="i",ylab=
'density',xlab='',main="The Beta Density Distribution") # 画出概率密度函数曲线,如图1-28所示
lines(x,dbeta(x,5,1),col="green")
lines(x,dbeta(x,1,3),col="blue")
lines(x,dbeta(x,2,2),col="orange")
lines(x,dbeta(x,2,5),col="black")
legend("top",legend=paste("a=",c(.5,5,1,2,2)," b=", c(.5,1,3,2,5)), lwd=1,col=c("red", "green","blue","orange","black"))
2.?累积分布函数
贝塔分布的累积分布函数公式为(1.32):

(1.32)其中B是正则不完全贝塔函数。
下面的R程序画出贝塔分布的累积分布函数曲线。
set.seed(1)
x<-seq(-5,5,length.out=10000)
y<-pbeta(x,0.5,0.5) # 计算服从贝塔分布B(0.5,0.5),10000个点的累积分布函数的值plot(x,y,col="red",xlim=c(0,1),ylim=c(0,1),type='l',xaxs="i", yaxs="i",ylab=
'F(x)',xlab='',main="The Beta Cumulative Distribution Function") # 画出累积分布函数曲线,如图1-29所示
lines(x,pbeta(x,5,1),col="green")
lines(x,pbeta(x,1,3),col="blue")
lines(x,pbeta(x,2,2),col="orange")
lines(x,pbeta(x,2,5),col="black")
legend("topleft",legend=paste("a=",c(.5,5,1,2,2)," b=", c(.5,1,3,2,5)), lwd=1,col=c("red", "green","blue","orange","black"))

3.?分布检验
对于贝塔分布,Kolmogorov-Smirnov连续分布检验的原假设为H0:数据集符合贝塔分布,备择假设为H1:样本所来自的总体分布不符合贝塔分布。
set.seed(1)
S<-rbeta(1000,1,2)
ks.test(S, "pbeta",1,2) # Kolmogorov-Smirnov检验One-sample Kolmogorov-Smirnov test
data: S
D = 0.0202, p-value = 0.807
alternative hypothesis: two-sided
这里D值很小,p值>0.05,不能拒绝原假设,所以数据集S符合形状参数为1和2的贝塔分布!
在掌握了这几种常用的连续型分布后,我们就可以基于这些分布来建模了,很多算法模型也就能解释通了!最后说明一点,本书不是统计学方面的教科书,对每种分布的定义均摘自互联网,与教科书有出入的部分请以统计学教科书为准。






















