只用python求向量内积 python 向量内积

转载

mob64ca140530fb 2024-03-14 07:45:14

文章标签 只用python求向量内积深度学习花书矩阵乘积向量相乘 文章分类 Python 后端开发

前言

向量

定义

与矩阵的关系

向量的乘法运算

矩阵

定义

矩阵乘积运算

Python代码

区别与联系

举例

总结

重点区别

点积与矩阵相乘的联系

前言

看“花书”的过程中碰到这样一句话

两个相同维数的向量x 和y 的点积（dot product）可看作是矩阵乘积x⊤y。

明明在讲矩阵相乘，怎么又扯到点积了？还有向量……

之前学得懵懵懂懂，为了深度学习，我仔细找资料写下这篇博客，送给与我一样情况的小伙伴。

PS:“花书”为图书AI圣经《深度学习》，由全球知名的三位专家 Ian Goodfellow、Yoshua Bengio 和 Aaron Courville联合撰写，是深度学习领域奠基性的经典教材。

向量

定义

向量是一列数。

举例：向量

只用python求向量内积 python 向量内积_深度学习

只用python求向量内积 python 向量内积_矩阵乘积_02

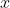
与矩阵的关系

向量可以看作只有一列的矩阵

向量的转置可以看作是只有一行的矩阵

向量x的转置:

只用python求向量内积 python 向量内积_深度学习_03

向量的乘法运算

向量有很多运算，本文只说向量的乘法运算。

数量积（又叫内积、点积dot product; scalar product）

设二维空间内有两个向量
和
，定义它们的数量积（又叫内积、点积）为以下实数：
更一般地，n维向量的内积定义如下：

参考百度百科

矩阵

定义

矩阵是一个二维数组

矩阵乘积运算

矩阵有很多运算，本文只说矩阵乘积运算。

设A为
的矩阵，
B
为
的矩阵，那么称
的矩阵
C
为矩阵
A
与
B
的乘积，记作
，
其中矩阵C中的第行第列元素可以表示为：

矩阵相乘的前提条件：

矩阵A 的形状是

$m\times p$

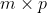
，矩阵B 的形状是

$p\times n$

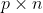
，C 的形状是

$m\times n$

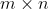
有两个矩阵A, B如下：

矩阵A的维数为3x2，矩阵B的维数为2x3，那么A、B相乘的结果矩阵C应该为3x3，其中m=3，p=2，n=3

只用python求向量内积 python 向量内积_矩阵乘积_18

根据公式

只用python求向量内积 python 向量内积_矩阵乘积_19

，其中i, j取值范围为[1, 3], p=2

得出矩阵C各个元素为如下表格

只用python求向量内积 python 向量内积_花书_20

即矩阵C为3x3的矩阵

只用python求向量内积 python 向量内积_向量相乘_21

简单地记：结果矩阵C的第(i, j)个元素为矩阵A的第 i 行与矩阵B的第 j 列分别相乘后求和的结果。

Python代码

写了一个简单的矩阵乘积方法，与np.dot(A, B, C)的结果是一样的。供参考。

以下方法的缺点是没法进行大数字的矩阵计算，比如A的维数为1000*10000，B的维数为10000*10000的情况.还需要再改进。

np.dot(A, B, C)也不能进行这么大数字的矩阵计算。

各位如果有更好的方法欢迎留言。

#! /usr/bin/env python
# -*- coding: utf-8 -*-

import numpy as np


def dot(A, B):
    row = A.shape[0]
    column = B.shape[1]
    p = A.shape[1]
    if A.shape[1] != B.shape[0]:
        return
    # 创建一个矩阵C，维数为row*column, 其值全部为零
    C = np.zeros((row, column), dtype=A.dtype)
    print("A.shape, B.shape, C.shape:", A.shape, B.shape, C.shape)
    # 计算矩阵相乘结果
    for i in range(row):
        for j in range(column):
            for k in range(p):
                C[i, j] += A[i, k] * B[k, j]
    return C


if __name__ == '__main__':
    A = np.arange(3, 9).reshape(2, 3)
    B = np.arange(1, 7).reshape(3, 2)
    C = np.zeros((2, 2), dtype=int)
    print("matrix A:\n", A)
    print("matrix B:\n",B)
    np.dot(A, B, C)
    print("np.dot C:\n", C)

    c = dot(A, B)
    print("my dot C:\n", c)
    assert C.any() == c.any()
    assert C.all() == c.all()