离散概率分布,即离散型随机变量的概率分布,与其相对的是连续概率分布。显然,离散往往意味着与自然数密切相关,本文下面介绍几种常见的离散概率分布及其Python运用。
一、离散均匀分布:掷骰子
均匀分布分为离散与连续两种情况,这里介绍离散的情况。离散型均匀分布指有限个数值拥有相同的概率的分布,比如掷骰子。假设实验结果共有n种可能,其分布列为
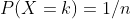
,即每种情况发生的可能性相同。
二、二点分布(伯努利分布):扔一次硬币
二点分布,又称伯努利分布。用 X 代表扔一次硬币的结果,正面则 X 取1,反面则 X 取0,该硬币扔出正面的概率为p,其分布列为
。数学期望为p。注意到一般不用分类函数表示二点分布的分布列,上述表达形式在 Logistic 回归的最大似然估计中有用。
三、二项分布:扔 n 次硬币中正面的次数
二项分布是多种离散分布的基础,用 X 代表扔 n 次硬币的结果中正面的次数,该硬币扔出正面的概率为p,其分布列为
。即先从 n 次结果中随机选出 k 次作为正面,乘以 k 次正面的概率再乘 n - k 次反面的概率。数学期望为 np ,即简单的次数乘以每次期望。
四、几何分布:扔多次硬币第一次出现正面的次数
用 X 代表扔多次硬币在第一次出现正面时扔的次数,该硬币扔出正面的概率为p,其分布列为
。即前 k - 1 次均为反面,最后一次为正面的概率。数学期望为 1 / p,即正面概率的倒数。
这样看来,几何分布似乎与几何无关?为什么叫几何分布呢?这是由于其分布列是一个等比数列,而等比数列又被称为几何数列。那等比数列又缘何被称为几何数列呢?这是因为等比数列的中间项是前后两项的几何平均数。
五、负二项分布:扔多次硬币第 r 次出现正面的次数
用 X 代表扔多次硬币在第 r 次出现正面时扔的次数,该硬币扔出正面的概率为p,其分布列为
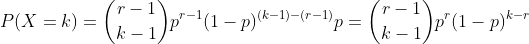
。
由于最后一次一定是正面,因此先从前 k - 1 次中随机选出 r - 1 次作为正面,乘以 r 次正面的概率再乘 k - r 次反面的概率。数学期望为 r / p,即出现正面的次数除以正面概率。
几何分布是负二项分布的特例。
六、超几何分布:有限总体不放回抽样
假设一个袋子里有 M 个球,其中有 N 个红球,从袋子里一次性随机摸 n 个球,用 X 代表其中红球的个数,则 X 的分布列为
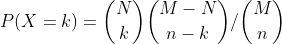
。
即先从 N 个红球中选 k 个出来,再从 M - N 个非红球中选 n - k 个出来,这样组成了 n 个球中有 k 个红球的完备情况,再除以从 M 个球中抽取 n 个球的总情况即得到概率。数学期望为 Nn / M,即抽取一个红球的概率乘以抽取个数。
七、泊松分布:二项分布的极限情况
泊松分布是二项分布在单位时间内取极限的情况,即假设每个单位时间里事件发生的次数均服从二项分布,在单位时间趋于 0 时事件发生的次数就服从泊松分布。
首先将时间分成 n 段,每段 1 / n,假设事件发生的概率与时长是线性关系,则
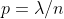
,
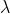
是系数。此时,每段的事件发生次数服从二项分布,
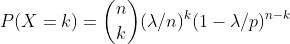
。再对 n 求极限,有
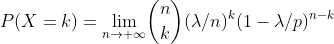
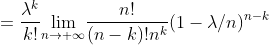
注意到,
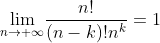
,这是由于分子分母均为 k 项。
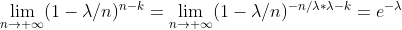
综上,
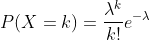
,其中
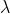
为单位时间内事件发生的平均次数,所以数学期望即为
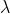
。
八、用 Python 生成上述分布随机数
from scipy.stats import randint, bernoulli, binom, geom, nbinom, hypergeom, poisson
###########生成随机数###########
randint.rvs(1, 10, size=100) # 1 到 9 的均匀离散分布随机数 100 个
bernoulli.rvs(p=0.3, size=100) # p = 0.3 的伯努利分布随机数 100 个
binom.rvs(n=100, p=0.6, size=10) # n=100, p=0.6 的二项分布随机数 10 个
geom.rvs(p=0.4, size-100) # p = 0.4 的几何分布随机数 100 个
nbinom.rvs(n=100, p=0.6, size=10) # r=100, p=0.6 的负二项分布随机数 10 个
hypergeom.rvs(M=100, n=10, N=20, size=10) # M=100, n=10, N=20 的超几何分布随机数 10 个
poisson.rvs(mu=1, size=100) # lambda=1 的泊松分布随机数 100 个
###########计算概率###########
randint.pmf(k=2, 1, 10) # 1 到 9 的均匀离散分布等于 2 的概率
bernoulli.pmf(k=1, p=0.3) # p = 0.3 的伯努利分布等于 1 的概率
binom.pmf(k=2, n=100, p=0.6) # n=100, p=0.6 的二项分布等于 2 的概率
geom.pmf(k=2, p=0.4) # p = 0.4 的几何分布等于 2 的概率
nbinom.pmf(k=2, n=100, p=0.6) # r=100, p=0.6 的负二项分布等于 2 的概率
hypergeom.rvs(k=2, M=100, n=10, N=20) # M=100, n=10, N=20 的超几何分布等于 2 的概率
poisson.pmf(k=2, mu=1) # lambda=1 的泊松分布等于 2 的概率
###########累积分布函数###########
randint.cdf(k=2, 1, 10) # 1 到 9 的均匀离散分布小于等于 2 的概率
bernoulli.cdf(k=1, p=0.3) # p = 0.3 的伯努利分布小于等于 1 的概率
binom.cdf(k=2, n=100, p=0.6) # n=100, p=0.6 的二项分布小于等于 2 的概率
geom.cdf(k=2, p=0.4) # p = 0.4 的几何分布小于等于 2 的概率
nbinom.cdf(k=2, n=100, p=0.6) # r=100, p=0.6 的负二项分布小于等于 2 的概率
hypergeom.cdf(k=2, M=100, n=10, N=20) # M=100, n=10, N=20 的超几何分布小于等于 2 的概率
poisson.cdf(k=2, mu=1) # lambda=1 的泊松分布小于等于 2 的概率除了上述的 rvs 方法生成随机数、pmf 求概率密度、cdf 求累积概率之外,还有 stats 求矩、median 求中位数等方法





















