贝叶斯深度学习实现代码贝叶斯网络训练

转载

墨染心语 2024-01-17 06:57:42

文章标签 贝叶斯深度学习实现代码机器学习朴素贝叶斯算法贝叶斯网络概率分布 文章分类 深度学习人工智能

Advanced Topics in Statistical Machine Learning 笔记02：贝叶斯网络（Bayesian Network）

贝叶斯网络构建

网络结构（Network Structure）

马尔科夫假设（Markovian Assumptions）

参数化（Parametrisation）
网络定义（Network Definition）

独立性属性（Properties of Independence）

对称 (Symmetry)
分解 (Decomposition)
弱联合（Weak Union）
收缩 (Contraction)
交集（Intersection）

独立性的图形测试（Graphical Test of Independence）

D-Separation
对于 D-Separation 的检测
可靠性和完备性（Soundness and Completeness）
独立关系图（Independence Maps）

I-MAP
D-MAP
P-MAP

马尔科夫毯（Markov Blanket）

我们首先回顾一下贝叶斯网络 (Bayesian Networks) 的作用。我们之前已经提到过，在进行概率计算，尤其是实际情况的概率推理时，联合概率分布表 (Joint Probability Distribution Table) 是个十分常见的手段，因为我们需要考虑所有的情况。但是这个表有一个很大的问题，那就是它的规模会根据变量的数量指数级增长，因为一般都是二值变量，所以联合概率的规模一般为 2ⁿ。显然，这对于存储空间造成了很大的压力，同时也对建模和计算造成困难。因此，我们使用贝叶斯网络的一个很重要的原因，就是为了避免这些问题。其次，联合概率分布会隐藏一些相关属性，比如独立性等，而贝叶斯网络能够体现这些特性。

贝叶斯网络构建

网络结构（Network Structure）

在上一篇笔记中，我们已经对贝叶斯网络的结构进行了一个基本的介绍，这里，我们先回顾一下，依然是用一个简单的例子来进行理解：

首先，贝叶斯网络是一种 DAG (Directed Acyclic Graph)，即有向无环图。在这幅图中：

节点 (Nodes) 表示变量 (Variables)
边 (Edge) 可以表示因果关系 (Direct Causal Influence)。我们目前这样理解就好，后面随着介绍的深入，我们会体会到边代表的具体内容。 比如，下图我们理解为：警报 (Alarm) 被触发，导致邻居来电 (Call)

贝叶斯深度学习实现代码贝叶斯网络训练_朴素贝叶斯算法

在这种表述形式下，我们发现，实际上，即使不是被边直接相连的两个变量，也会受到影响。比如：我们在广播 (Radio) 上听到有关地震的报道，这就增加了我们居住的地区发生地震 (Earthquake) 的可能性，进一步也就加大了警报 (Alarm) 被地震触发的几率，最终也就增加了邻居呼叫 (Call) 我们的几率。但是，这种“影响” (Influence) 在我们已观察到某些变量时，是会被“阻碍” (Blocked) 的。

为了方便理解，我们可以把“影响” (Influence) 看作是水，把每个变量 (图中的节点) 看作是阀门，当某个变量被观察 (Observed) 时，也就意味着我们已经对它的信息有所确知，因此该变量对应的节点/阀门就被关闭了，“影响”也就无法继续流到后面。

比如，我们已经知道警报 (Alarm) 没有被触发。这可能有很多原因，可能是地震 (Earthquake) 强度不足以触发警报、入室抢劫 (Burglary) 很隐秘没有触发或是其他情况，但我们不需要关心这些事情，我们只需要知道，邻居给我们打电话 (Call) 的概率不会受任何变量影响了，因此可以知道 𝐶 ⊥ 𝑅|¬𝐴.

根据以上介绍，我们能够知道，DAG G 表示以下独立性陈述：

𝑉 ⊥ 𝑁𝑜𝑛_𝐷𝑒𝑠𝑐𝑒𝑛𝑑𝑎𝑛𝑡𝑠 𝑉 | 𝑃𝑎𝑟𝑒𝑛𝑡𝑠(𝑉)

Parent(V)：表示变量/节点 V 的父节点
Descendants(V)：表示变量/节点 V 的所有后续节点
Non_Descendants(V)：所有其他的节点

在本例中，能够得到 A ⊥ R | E, B 等一系列的独立关系陈述。这一系列从贝叶斯网络 G 中得到的独立关系陈述就被称为马尔科夫假设 (Markovian Assumptions) ，记作 Markov(G).

马尔科夫假设（Markovian Assumptions）

为了便于理解马尔科夫假设，这里我们依旧把 DAG(G) 看作是因果结构 (Causal Structure)，那么 Parent(V) 就表示 V 的直接原因，Descendants(V) 则可以表示 V 的的影响对象。马尔科夫假设的核心思想就是 “在已知某个变量的直接原因的情况下，除了与其关联的变量之外，不会被其他任何变量所影响”

𝑉 ⊥ 𝑁𝑜𝑛_𝐷𝑒𝑠𝑐𝑒𝑛𝑑𝑎𝑛𝑡𝑠 𝑉 | 𝑃𝑎𝑟𝑒𝑛𝑡𝑠(𝑉)

因此，在我们之前的例子中，可以得到如下结论：
𝐶 ⊥ 𝐵, 𝐸, 𝑅 | 𝐴
𝑅 ⊥ 𝐴, 𝐵, 𝐶 | 𝐸
𝐴 ⊥ 𝑅 | 𝐵, 𝐸
𝐵 ⊥ 𝐸, 𝑅
𝐸 ⊥ 𝐵

这里我们需要着重注意的一点是，Markov(G) 只是确保了 DAG G 中的独立关系 (Independence) 满足了我们的要求，但是对于满足这样一系列独立关系的一幅图，可能会有多种不同的概率分布。这就是为什么我们需要给每一个变量/节点，维护一个 CPT (Conditional Probability Table)，只有这样才能确保定义一个唯一的概率分布。

目前为止，我们一直把 “因果关系 (Causality) ” 作为边 (Edge) 的解释，这是为了更容易进行建模和理解。但是实际上，关于贝叶斯网络 (Bayesian Network) 的定义本身，并没有涉及到任何与“因果关系”相关的表述，它实际上只是我们这里用来方便理解的工具而已。这里我们看一个具体的例子：

贝叶斯深度学习实现代码贝叶斯网络训练_朴素贝叶斯算法_02

这两个贝叶斯网络中，第一个就是我们之前使用了“因果关系”来理解并搭建的网络，而第二个网络并未使用所谓的“因果关系”。实际上，或许你会感到奇怪，但这两幅图所表示的变量之间的独立性状态是完全相同的。这在阅读了整篇笔记之后，我相信你能够完全理解。

参数化（Parametrisation）

参数化 (Parametrisation) 会量化节点和其父节点之间的依赖关系。实际体现就是对于 DAG G 中的每个节点会维护一个 CPT (条件概率表)，这个表中会包含节点 V 本身和其所有父节点 U。

贝叶斯深度学习实现代码贝叶斯网络训练_机器学习_03

这里我们要注意一个很重要的性质，也是条件概率本身的一个重要公式：

贝叶斯深度学习实现代码贝叶斯网络训练_朴素贝叶斯算法_04

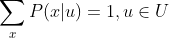
因为这个重要的性质，可以大大减少我们在建模时，对于参数的需求量，比如，因为 P(a|b) + P(a|¬b) = 1，所以在建模是，我们只需要其中一者即可。因此，上面图例中的贝叶斯网络，我们总共只需要 1 + 2 + 4 + 2 + 2 = 11 个参数/概率即可。从参数数量上，我们能够具体体会到之前说过的 “贝叶斯网络比联合概率表 (Joint Probability Matrix) 更加节省空间”，该例子中共有 5 个变量，若使用后者，共需要保存一个 2⁵ = 32 个联合概率的概率表，空间需求大大增加。

网络定义（Network Definition）

现在，贝叶斯网络中的所有独立性关系以及唯一的概率分布都被确定，整个网络的搭建也就完成了。因此，一个针对变量 Z 的贝叶斯网络表示为 (G, Θ) :

G 就是一个变量集合 Z 构成的有向无环图 (DAG)，被称为网络结构 (Network Structure)
Θ 是一系列的条件概率表 (CPT)，每一张表对应 Z 中的每一个变量，被称为网络参数化 (Network Parametrisation)

我们使用：

Θ_X|U 表示变量 X 和它的父节点 U 的 CPT
XU 表示一系列变量，这一系列变量也被称为网络家庭 (Network Family)，父母和孩子
θ_x|u 表示 P(x|u) 的值，也被称为网络参数 (Network Parameter)

网络实例化 (Network instantiation) 就是对所有网络变量的一组赋值。用 θ_x|u ~ z 表示网络参数复兴实例化 z。下面给出一个实例化例子：

贝叶斯深度学习实现代码贝叶斯网络训练_概率分布_05

根据以上实例化选择的网络参数如下图所示：

贝叶斯深度学习实现代码贝叶斯网络训练_概率分布_06

根据之前对于贝叶斯网络的定义，我们可以知道：只有一个概率分布满足贝叶斯网络所施加的约束。这个独一无二的概率分布就是：

贝叶斯深度学习实现代码贝叶斯网络训练_贝叶斯网络_07

最后，我们再来看一下贝叶斯网络的复杂度。我们都知道，复杂度就是要考虑最坏的情况，贝叶斯网络也不例外。我们把所有变量的父节点数量最大值记为 k，那么单个 CPT Θ_X|U 的最大尺寸即为 O(d^k+1)，如果该网络共有 n 个变量，那么总共就是 O(nd^k+1)，即最大 CPT 乘以变量数量。以上面的图为例：

Biggest CPT size: O(d^k+1) = O(2²⁺¹) = 8
Total is bounded by: O(nd^k+1) = 5 * 8 = 40

独立性属性（Properties of Independence）

我们之前已经了解到，由贝叶斯网络 (G, Θ) 指名的概率分布 P，满足 Markov(G) 中的独立性关系。但是，这并不是全部，我们之前的例子中，可以根据其马尔科夫假设得到以下独立关系：

𝐶 ⊥ 𝐵, 𝐸, 𝑅 | 𝐴
𝑅 ⊥ 𝐴, 𝐵, 𝐶 | 𝐸
𝐴 ⊥ 𝑅 | 𝐵, 𝐸
𝐵 ⊥ 𝐸, 𝑅
𝐸 ⊥ 𝐵

但是，这个网络中实际上还有其他的独立关系。比如 𝑅 ⊥ 𝐴 | 𝐸，我们并没有根据马尔科夫假设直接得到这个关系。但是，我们必须要知道，马尔科夫假设是一个网络中最基础的独立性集合，其他的独立性都能从中推论而来，而这个推论的过程，就需要用到独立性的一些特性，这些特性也被称为石墨公理 (Graphoid Axioms)，它包括对称 (Symmetry)，分解 (Decomposition)，弱联合 (Weak Union) 和收缩 (Contraction) 这几个特性实际上很好理解，接下来就对它们进行一个直觉的介绍。

对称 (Symmetry)

对称性是独立性最简单的一个特性：

𝑿 ⊥ 𝒀 | 𝒁 if and only if 𝒀 ⊥ 𝑿 | 𝒁

𝐴 ⊥ 𝑅 | 𝐵, 𝐸 (Markovian property for 𝐴)
𝑅 ⊥ 𝐴 | 𝐵, 𝐸 (Using symmetry)

分解 (Decomposition)

这个特性也很好理解。如果我们已经知道 YW 不会对我们对于 X 的信念度造成影响，那么 Y 和 W 也无法单独对 X 造成影响。

𝑿 ⊥ 𝒀 ∪ 𝑾 | 𝒁 only if 𝑿 ⊥ 𝒀 | 𝒁 and 𝑿 ⊥ 𝑾 | 𝒁

𝑅 ⊥ 𝐴, 𝐶, 𝐵 | 𝐸 (Markovian property for 𝐴)
𝑅 ⊥ 𝐴 | 𝐸 (using decomposition)
𝑅 ⊥ 𝐶 | 𝐸 (using decomposition)
𝑅 ⊥ 𝐵 | 𝐸 (using decomposition)

𝑋 ⊥ 𝑾 for every 𝑾 ⊆ Non_Descendants(𝑋)

分解性也能够帮助我们证明贝叶斯网络的链式法则 (Chain)

根据贝叶斯网络的定义，我们可以得到：
𝑃(𝑒, 𝑏, 𝑟, 𝑎, 𝑐) = 𝑃(𝑒) 𝑃(𝑏) 𝑃(𝑟|𝑒) 𝑃(𝑎|𝑒, 𝑏) 𝑃(𝑐|𝑎)
根据链式法则，我们能得到：
𝑃(𝑒, 𝑏, 𝑟, 𝑎, 𝑐) = 𝑃(𝑒) 𝑃(𝑏|𝑒) 𝑃(𝑟|𝑏, 𝑒) 𝑃(𝑎|𝑒, 𝑏, 𝑟) 𝑃(𝑐|𝑎, 𝑒, 𝑏, 𝑟)

According to P(b) and P(b|e): B ⊥ E
Markov assumption: B ⊥ E, R. Using decomposition: B ⊥ E & B ⊥ R

According to P(r|e) and P(r|b, e): R ⊥ B | E
Markov assumption: R ⊥ B, A, C | E. Using decomposition: R ⊥ B | E & R ⊥ A | E & R ⊥ C | E

贝叶斯深度学习实现代码贝叶斯网络训练_贝叶斯网络_08

弱联合（Weak Union）

如果我们已经知道 YW 不会对我们对于 X 的信念度造成影响，那么部分信息 Y 也不会让剩下的部分 W 对 X 造成影响。

𝑿 ⊥ 𝒀 ∪ 𝑾 | 𝒁 only if 𝑿 ⊥ 𝑾 | 𝒁 ∪ 𝒀

𝐶 ⊥ 𝐵, 𝐸, 𝑅 | 𝐴 (Markovian property for 𝐴)
𝐶 ⊥ 𝑅 | 𝐴, 𝐵, 𝐸 (using decomposition)

这可以看作是 Markov(𝐺) 得出的独立性的加强版。

收缩 (Contraction)

这个特性的理解可能会稍显复杂，它的定义是：在知道 Y 为无关信息且 W 也与 X 无关之后，那么 YW 一定也与 X 无关。

𝑿 ⊥ 𝒀 | 𝒁 and 𝑿 ⊥ 𝑾 | 𝒁 ∪ 𝒀 only if 𝑿 ⊥ 𝒀 ∪ 𝑾 | 𝒁

这一特性的证明会稍微复杂一些，我们用一个新的更简单的网络：

贝叶斯深度学习实现代码贝叶斯网络训练_贝叶斯深度学习实现代码_09

根据马尔科夫假设可得：X₃ ⊥ X₁ | X₂
X₃ ⊥ X₁ | X₂ = X₁⊥ X₃ | X₂ (Symmetric)

根据马尔科夫假设可得：X₄ ⊥ X₁ , X₂ | X₃
X₄ ⊥ X₁ , X₂ | X₃
= X₄ ⊥ X₁ | X₃ , X₂ (Weak Union)
= X₁⊥ X₄ | X₃ , X₂ (Symmetric)

X₁⊥ X₄, X₃| X₂

交集（Intersection）

该特性的核心思想为：如果我们知道给定 Y 时，信息 W 与 X 不相关，并且给定 W 时，信息 Y 与 X 不相关，那么 YW 与 X 不相关。

𝑿 ⊥ 𝒀 | 𝒁 ∪ 𝑾 and 𝑿 ⊥ 𝑾 | 𝒁 ∪ 𝒀 only if 𝑿 ⊥ 𝒀 ∪ 𝑾 | 𝒁

需要特别注意的是，这个特性只适用于严格正分布 (Strictly Positive Distributions) ，所谓严格正分配，指的是不会有为 0 的概率，这也意味着不会有为 1 的概率，因此，严格正分配实际上就表示不会有完全确知概率。

这里我们用一个电路图来进行理解：

贝叶斯深度学习实现代码贝叶斯网络训练_机器学习_10

E ⊥ A | C
E ⊥ C | A
在本例中 𝒁 = ∅ ，所以可以得到：
E ⊥ A, C
但是，这个结论是不正确的，这意味着这个电路的输出和左半边的电路完全没有关系，显然这不可能。造成这个结果的原因就在于，电路图的概率分布不是严格正分布，它一定包含确知概率。

独立性的图形测试（Graphical Test of Independence）

我们现在已经知道，根据贝叶斯网络 (G, Θ) 的 Markov(G) ，我们可以通过之前介绍的一系列石墨公理 (Graphoid Axioms) 推论出其中的所有独立关系，但是这个过程会显得比较复杂。这里，我们介绍一个更加简单的方式来找到这些独立关系，这种方式直接使用图来进行测试，十分直观和简单，被称为 D-Separation。

D-Separation

我们假设三个变量 X, Y 和 Z 。如果变量 X 和 Y 被 Z D-Separation，那么就意味着在 DAG G 中，节点 X 和节点 Y 之间的每一条路径都会被 Z 阻断，因此对于从 DAG G 得到的所有概率分布，都满足 𝑿 ⊥ 𝒀 | 𝒁

为了便于理解，我们来回顾一下之前我所做的一个比喻，将节点看作 “阀门”，将 “影响” 看作是管道中流动的水。这个思想将帮助我们更好地理解 D-Separation 的概念。那么，首先我们来看一看，整个 “管道系统” 中会有哪些不同的 “阀门”。

一般来说，总共有 3 种不同的阀门：

贝叶斯深度学习实现代码贝叶斯网络训练_机器学习_11

我们用 Z 表示已被观察到的节点集合，也就是我们所谓的证据 (Evidence)

名称	意义	关闭条件
顺序阀 (sequential valve)	N₁ → W → N₂：W 是它的原因 N₁ 和它的影响 N₂ 的中介 (Intermediary)	如果 W 出现在 Z 中，则顺序阀关闭
分歧阀 (divergent valve)	N₁ ← W → N₂：W 是 N₁ 和 N₂ 的共同原因 (Common Cause)	如果 W 出现在 Z 中，则分歧阀关闭
收敛阀 (convergent valve)	N₁ → W ← N₂：W 两个原因 N₁ 和 N₂ 的共同结果 (Common Effect)	如果 W 和其任何后继节点都没有出现在Z 中，则收敛阀关闭

在有了以上这些信息之后，我们要做的就只有将整个通路分割为一段段来进行检查，只要有一段通路的阀门关闭，则整条通路就一定是关闭的，此时就达成了 D-Separation，也就得到了独立性关系。

接下来，我们还是用之前的地震警报的贝叶斯网络，来看几个具体的例子：

贝叶斯深度学习实现代码贝叶斯网络训练_朴素贝叶斯算法

Case 1：X = R, Y = C, Z = Ø
首先检查有无通路。若 R 和 C 之间没有通路，那么 R 和 C 一定独立，但此处存在通路 R - E - A - C.
通路的第一部分为 R ← E → A 的分歧阀，E 未被观察到，即 E 不在 Z 中，因此通路为 Open
通路的第二部分为 E → A → C 的顺序阀，A 未被观察到，即 A 不在 Z 中，因此通路为 Open
因此整条通路允许 “影响” 流通，所以 R 和 C 不满足 D-Separation，此时，它们不独立

Case 2：X = R, Y = C, Z = E
这是的情况和之前只改变了一点，那就是 E 被观察到了，即 E 在 Z 中，那么我们知道，R ← E → A 的分歧阀为 Close，整条路径不通。因此 R 和 C 满足 D-Separation，所以 R ⊥ C | E

Case 4：X = R, Y = B, Z = Ø
首先确认， R 和 B 之间有路径
第一部分为 R ← E → A 的 Divergent，因为 E 为Open，通路。
第二部分为 E → A ← B 的 Convergent，因为 A 或 A 的后继都不在 Z 中，因此 Close，不通，所以 R 和 B 满足 D-Separation，因此 R ⊥ B

Case Five：X = R, Y = B, Z = A
第一部分和上述 Case 4 相同，第二部分因为 A 在 Z 中，所以Open，所以 R 和 B 不满足 D-Separation

对于 D-Separation 的检测

我们根据 D-Separation 的定义可以知道，想要检测在 DAG G 中， X 和 Y 是否被 Z D-Separation，其实就是在看 X 和 Y 是否在一幅新的图 G’ 中不相连

具体的操作很简单，我们把 G 中所有不属于 X ∪ Y ∪ Z 的叶节点 (Leaf Node) 全部删除，直到删无可删。之后，再把所有来自 Z 中的边全部删除，此时，如果 X 和 Y 不相连，那么满足 D-Separation。

贝叶斯深度学习实现代码贝叶斯网络训练_贝叶斯网络_13

比如我们想要检测 T,C 是否和 B 被 S,X D-Separation。此时，X = {T, C}, Y = {B}, Z = {S, X}
首先，我们删除叶节点，因为 X 在 X ∪ Y ∪ Z 中，因此，我们只能删除 D 以及它的两条边
此时叶节点只剩 X 和 B，它们都在 X ∪ Y ∪ Z 中，无法继续删除
删除所有来自 Z 中的边，即从 S 出发的两条边，这时我们已经能看到，T,C 和 B 没有路径相连，因此 T,C 与 B 满足D-Separation

可靠性和完备性（Soundness and Completeness）

直接看结论：

D-Separation 是可靠的 (Sound) 。如果 P 是由贝叶斯网络 (G, Θ) 的概率分布，那么只有 𝑿 ⊥ 𝒀 | 𝒁，才有 dsep(X, Z, Y)。我们可以放心地使用 D-Separation 来推导 P 中的独立性陈述。
D-Separation 不是完备 (Complete) 的。它无法推断出 P 中的所有独立性陈述。因为有一些独立性隐藏在网络的参数之中。

贝叶斯深度学习实现代码贝叶斯网络训练_贝叶斯网络_14

比如在上图这个例子中，我们可以看到，在这个参数化下，A 的取值不会影响 B，B ⊥ A。但是这个独立性是无法用 D-Separation 推论出来的，因为 A 和 B 两个节点是直接相连的。

造成这一结果的原因其实非常简单，这源于 D-Separation 本身的性质，我们之前说过 D-Separation 是一种 “图形测试方法”，我们是根据网络的图形特性来进行推论的，因此对于具体的参数化，这一“数”的领域，难以触及。

因此，我们可以得到如下结论，给定一个从贝叶斯网络 (G, Θ) 得出的分布 P ：

如果变量 X 和 Y 被 Z D-Separation ，那么给定Z，X 和 Y 相互独立对于所有的参数化都成立
如果变量 X 和 Y 不被 Z D-Separation，那么给定Z，X 和 Y 是否相互独立取决于具体的参数化 Θ

当然，我们在对贝叶斯网络进行参数化时候，也可以人为保障 D-Separation 的完备性，比如我们规定：对于每一个 DAG G，都有一个参数化 Θ 使得 dsep(X, Z, Y) 当且仅当 𝑿 ⊥ 𝒀 | 𝒁。也就是人为限制参数化中，隐性独立关系的出现。这一举措也体现了我们并不能对 D-Separation 算法本身进行提升，因为这个算法是直接根据图进行的计算。

独立关系图（Independence Maps）

I-MAP

独立关系图 (Independence Map, I-MAP) 描述了 DAG 中的独立性与概率分布之间的关系，它有助于理解 DAG 作为独立声明语言的表达能力。

比如我们用 G 表示 DAG，P 表示相同变量的概率分布。那么 G 是 P 的独立关系图 (I-MAP)，当且仅当 dsep(X, Z, Y) only if 𝑿 ⊥ 𝒀 | 𝒁。这意味着 D-Separation 声明的每个独立性都在 P 中成立。

我们可以把所有能够从P中得到的独立性看作一个集合，那么 D-Separation 就是其子集。但这里我们并未限制 D-Separation 的尺寸，随着我们往 G 中添加 Edge，其尺寸可能会越来越小。当G变为一个全连接图 (Fully Connected Graph) ，很有可能 D-Separation 会变为一个空集，但此时它仍为 P 的 I-MAP，因为空集是任何集合的子集。

我们还定义最小的 (Minimal) 的 I-MAP。最小的 I-MAP 指的是，如果我们删除图 G 中的任意一条边，G 不再为 I-MAP ，那么此时的 G 就是最小的 I-MAP。因为删除任何一条边都意味着，增加了一部分独立性。

贝叶斯深度学习实现代码贝叶斯网络训练_机器学习_15