信息熵
信息熵 (information entropy)是度量样本集合纯度最常用的一种指标。假定当前样本集合
中的第
类样本所占的比例为
(k = 1,2...
), 则 D 的信息熵为
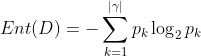
Ent(D) 的值越小,则D的纯度越高 .
- 计算信息熵时约定 : 如果 p = 0,则 = 0
- Ent(D)的最小值是0,最大值是
- |X| 表示X的数量,比如表示样本D的数量,下同.
假定随机变量X有两个取值0和1
X | 0 | 1 |
p(x) | p | 1-p |
则图像是,

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
x = np.arange(0,1,0.01)
y = -x*np.log2(x) -(1-x)*np.log2(1-x)
sns.set()
plt.grid(visible=True, which='major', linestyle='-')
plt.grid(visible=True, which='minor', linestyle='--', alpha=0.5)
plt.minorticks_on()
plt.xlabel('x')
plt.ylabel('H(x)')
plt.plot(x,y)
# plt.show()
plt.savefig('./h.png')条件熵
概率定义: 随机变量X在给定条件下随机变量Y的条件熵,公式如下,
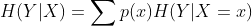
或者换一种符号表示,
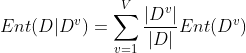
假定离散属性 a(西瓜的色泽)有V 个可能的取值{
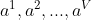
} (比如 {青绿,乌黑,浅白,墨绿 .. })等等吧 ,如果使用a 来对样本集D(西瓜) 进行划分 ,则会产生 V 个分支节点,其中第v 个分支节点包含了D 中所有在属性a上的取值为
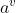
的样本 ,记作
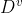
.
信息增益
根据信息熵的计算公式, 我们可以计算出
的信息熵 ,再考虑到不同的分支节点所包含的样本数不同,给分支节点赋予权重
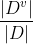
,也就是样本数越多的分支节点影响越大,于是可以计算出用 a 属性对样本D进行划分所获得的"信息增益"(information gain)
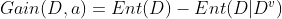
代入,
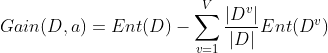
一般来说, 信息增益越大,则意味着使用属性a进行划分所获得的"纯度提升"越大 .因此可以用信息增益来进行决策树的划分属性选择.
下面以西瓜数据集为例, 该数据集包含17个样本,用以学习一棵能预测没刨开的是不是好瓜的决策树. 显然
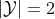
, 下图中可以看到,正例 占 8/17 , 反例占 9/17,
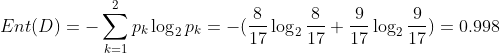

然后我们计算出当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感} 中每个属性的信息增益. 以属性"色泽" 为例 ,它有两个可能的取值 :{青绿,乌黑,浅白} .使用该属性对D进行划分, 则可得到 3个 子集 ,分别记为 D1 (色泽=青绿) D2(色泽=乌黑) D3(色泽=浅白).
子集D1 包含的编号{1,4,6,10,13,17} , 正例(是)占 p1 = 3/6 ,反例(否) 占 p2 = 3/6 ;
子集D2 包含的编号 {2,3,7,8,9,15} , 正例占 p1 = 4/6 , 反例占 p2 = 2/6 ;
子集D3 包含的编号 {5,11,12,14,16} ,正例占p1 = 1/5 , 反例占p2 = 4/5 ;
可计算出"色泽"划分之后所获得的信息熵为:

于是 , 计算出属性 " 色泽"的信息增益为 :

显然这里 Gain(D,纹理) = 0.381 信息增益最大, 于是他被选为划分属性.

然后,决策树学习算法将每一个分支节点做进一步划分. 以图中的一个分支节点("纹理= 清晰") 为例, 该节点包含的样例集合
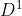
中有编号 {1,2,3,4,5,8,10,15} 的9 个样例,可用的属性集合为 { 色泽,根蒂,敲声,脐部,触感}; 基于
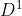
计算出各属性的信息增益:

"根蒂" , "脐部" , "触感" 3 个属性均取得最大的信息增益 ,可用选择其中一个作为划分属性, 最终得到:

增益率
事实上用信息增益准则对可取值数目较多的属性有所偏好,为了减少这种偏好可能带来的不利影响,我们会使用 "增益率" ,来选择最优划分属性 , 增益率定义为 :
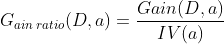
其中
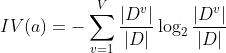
称为属性 a 的"固有值" ,属性a 取值数目越多(V越大) ,则 IV(a) 的值通常越大, 需要注意的是增益率准则对可取值数目较少的属性有所偏好,信息增益对可取值数目多的属性有所偏好, 折中一下就是先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择增益率最高的.
摘自 : 西瓜书























