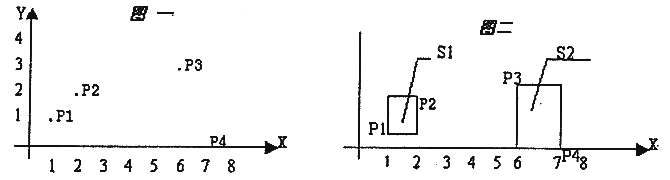NOIP 2002 矩形覆盖

题目描述

在平面上有 n 个点（n <= 50），每个点用一对整数坐标表示。例如：当 n＝4 时，4个点的坐标分另为：p1（1，1），p2（2，2），p3（3，6），P4（0，7），见图一。

这些点可以用 k 个矩形（1<=k<=4）全部覆盖，矩形的边平行于坐标轴。当 k=2 时，可用如图二的两个矩形 sl，s2 覆盖，s1，s2 面积和为 4。问题是当 n 个点坐标和 k 给出后，怎样才能使得覆盖所有点的 k 个矩形的面积之和为最小呢。约定：覆盖一个点的矩形面积为 0；覆盖平行于坐标轴直线上点的矩形面积也为0。各个矩形必须完全分开（边线与顶点也都不能重合）。
输入输出格式
输入格式：

n k xl y1 x2 y2 … …

xn yn （0<=xi,yi<=500)

输出格式：

输出至屏幕。格式为：

一个整数，即满足条件的最小的矩形面积之和。

输入输出样例
输入样例#1：

4 2
1 1
2 2
3 6
0 7

输出样例#1：

4

---

【分析】
枚举每个点放在哪一个矩形里…
剪枝：
1. 如果两个矩形重合，那么弹出
2. 如果当前点被某一个矩形覆盖，那么搜索下一层

---

【代码】

//NOIP 2002 矩形覆盖 
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define M(a) memset(a,0,sizeof a)
#define fo(i,j,k) for(i=j;i<=k;i++)
using namespace std;
const int mxn=55;
int n,k,ans=1e8;
int x[mxn],y[mxn],mxx[10],mnx[10],mxy[10],mny[10],vis[10];
inline int calc()
{
    int i,j,res=0;
    fo(i,1,k)
    {
        if(!vis[i]) return 1e8;
        res+=(mxx[i]-mnx[i])*(mxy[i]-mny[i]);
    }
    return res;
}
inline bool judge()
{
    int i,j;
    fo(i,1,k)
      fo(j,i+1,k)
        if(vis[i] && vis[j])
        {
            if(mnx[j]<=mxx[i] && mxx[i]<=mxx[j] && mny[j]<=mxy[i] && mxy[i]<=mxy[j]) return 0;
            if(mnx[j]<=mxx[i] && mxx[i]<=mxx[j] && mny[j]<=mny[i] && mny[i]<=mxy[j]) return 0;
            if(mnx[j]<=mnx[i] && mnx[i]<=mxx[j] && mny[j]<=mxy[i] && mxy[i]<=mxy[j]) return 0;
            if(mnx[j]<=mnx[i] && mnx[i]<=mxx[j] && mny[j]<=mny[i] && mny[i]<=mxy[j]) return 0;
        }
    return 1;
}
inline void dfs(int num)
{
    if(!judge()) return;
    if(num>n)
    {
        ans=min(ans,calc());
        return;
    }
    int i,j,tmp1,tmp2,tmp3,tmp4;
    fo(i,1,k)
      if(mnx[i]<=x[num] && x[num]<=mxx[i] && mny[i]<=y[num] && y[num]<=mxy[i])
      {
          vis[i]++;
          dfs(num+1);
          vis[i]--;
          return;
      }
    fo(i,1,k)
    {
        tmp1=mxx[i],tmp2=mxy[i],tmp3=mnx[i],tmp4=mny[i];
        mxx[i]=max(mxx[i],x[num]);
        mxy[i]=max(mxy[i],y[num]);
        mnx[i]=min(mnx[i],x[num]);
        mny[i]=min(mny[i],y[num]);
        vis[i]++;
        dfs(num+1);
        vis[i]--;
        mxx[i]=tmp1,mxy[i]=tmp2,mnx[i]=tmp3,mny[i]=tmp4;
    }
}
int main()
{
    int i,j;
    scanf("%d%d",&n,&k);
    fo(i,1,n)
      scanf("%d%d",&x[i],&y[i]);
    memset(mnx,0x3f,sizeof mnx);
    memset(mny,0x3f,sizeof mny);
    dfs(1);
    printf("%d\n",ans);
    return 0;
}