【算法排序】动态规划

目录

• 一、动态规划思想
• 二、动态规划与分治法的区别

• 1、共同点
• 2、不同点

• 三、动态规划特征

• 1、最优子结构
• 2、重叠子问题

• 四、动态规划求解问题的基本步骤
• 五、斐波那契数分析
• 六、实现思路
• 七、代码实现

一、动态规划思想

将待求问题划分为若干个子问题，按划分的顺序求解子阶段问题，前一个子问题的解，为后一个子问题的求解提供了有用的信息（最优子结构）。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其它局部解。依次解决各个子问题，最后求出原问题的最优解

二、动态规划与分治法的区别

1、共同点

二者都是求原问题具有最优子结构性质，都是将原问题分而治之，分解成若干个规模较小的子问题，然后将子问题的解合并，形成原问题的解

2、不同点

1、分治法：将问题分解成子问题后，通常是将子问题的解合并起来得到原问题的解
2、动态规划法：是先解决子问题，将子问题的解保存下来，最后根据子问题的解计算得到原问题的解

三、动态规划特征

1、最优子结构

问题的最优解是由最优子问题的最优解推出的，也就是问题的最优解包含了子问题的最优解

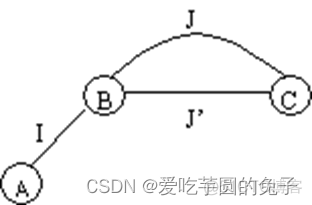
如图：若路线I和J是A到C的最优路径，则根据最优化原理，路线J必是从B到C的最优路线。

反证法证明： 假设有另一路径J是B到C的最优路径，则A到C的路径取I和J比I和J更优，矛盾：从而证明J`必是B到C的最优路径。最优化原理是动态规划的基础，任何问题，如果失去了最优化原理的支持，就不可能用动态规划方法计算哪些问题满足最优化原理

2、重叠子问题

在用递归算法自顶向下解问题时，每次产生的子问题并不是总是新问题。有些子问题被反复计算多次。斐波那契数列问题就存在重叠子问题。在递归实现中，当计算F(n)时，会先计算F(n-1)和F(n-2)，而计算F(n-1)时又会先计算F(n-2)和F(n-3)，这样就会出现重复计算的情况。

四、动态规划求解问题的基本步骤

动态规划所处理的问题是一个多阶段决策的问题，一般由初始状态开始，通过中间阶段决策的选择，达到结束状态。动态规划算法的代码设计都有一定的模式。一般经过以下几个步骤：
初始状态->决策1->决策2->…->决策n->结束状态

1. 找出最优解的性质，并刻画其结构特征（找问题状态）
2. 递归地定义最优值（找状态转移方程）
3. 自底向上地方式计算最优值
4. 根据计算最优值时得到的信息，构造最优解

五、斐波那契数分析

斐波那契数，通常用 F(n) 表示，形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
给定 N，计算 F(N)。

序列为：0、1
下标为：2
解释：F(2) = F(N - 1) + F(N - 2)= F(2 - 1) + F(2 - 2)=1+0 = 1
下标2的值为：1
序列为：0、1、1

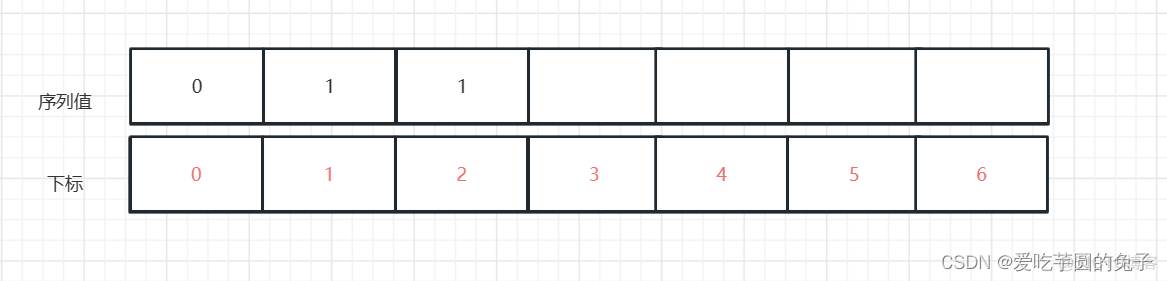
数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和（示意图如下）

六、实现思路

1. 定义一个要求的斐波那契数
2. 判断求的斐波那契数是否小于等于1，是的话直接返回求的斐波那契数，否的话，则创建一个数组，用来记录子问题的解
3. 初始化第一个斐波那契数值，和第二个斐波那契数值。求第三个斐波那契数值的时候，把前两个下标的值进行相加，得出第三个斐波那契的数值。依次按照这种方式，最终得出需要求的斐波那契数值

七、代码实现

public class Fibonacci {

    public static void main(String[] args) {
        int numberArr = 10; // 求第10个斐波那契数
        int result = fibonacci(numberArr); // 第10个斐波那契数的值
        System.out.println("第10个斐波那契数值为："+ result); // 输出第10个斐波那契数的值
    }
    /**
    * 斐波那契数列的动态规划算法
    * @paramn  第numberArr个斐波那契数，dp为数据处理后的值
    * @return 第numberArr个斐波那契数的值
    */
    public static int fibonacci(int numberArr) {
        if (numberArr <= 1) {
            // 当numberArr小于等于1时，直接返回numberArr
            return numberArr;
        }

        //创建数组，用于记录子问题的解
        //dp为数据处理后的值
        int[] dp = new int[numberArr + 1];
        dp[0] = 0; // 初始化第一个数
        dp[1] = 1; // 初始化第二个数

        // 递推求解子问题
        for (int i = 2; i <= numberArr; i++) {
            //dp[i]:i为该求下标的值
            //dp[i-1]:i为该求下标-1的值
            //dp{[i-2]:i为该求下标-2的值
            //算出两个下标的值后进行相加，最后得出该求下标的值
            dp[i] = dp[i - 1] + dp[i - 2];
            System.out.println("第"+i+"轮numberArr的值为"+ dp[i]);
        }
        // 返回第numberArr个斐波那契数的值
        return dp[numberArr];
    }
}