数据结构_树状数组 详解

数据结构_树状数组 详解

😀 Powerd By HeartFireY | -Binary Indexed Tree- |

文章目录

一、简介/前导

1.前导

我们来关注这样一个问题：要求对一个数组实现单点修改、区间求和。

我们不难得知：在朴素算法下，单点修改的时间复杂度$O(1)$，区间求和的时间复杂度$O(n)$。

如果使用前缀和进行优化，区间求和的时间复杂度降为$O(1)$，而单点修改的时间复杂度却变为$O(n)$。

显然，在强数据下，这两种算法是容易超出所给时间范围的。

如果我们使用一个数组来维护每一段区间的和，对所有需要用到的区间进行求和，但如果要查询或修改的区间跨度大，则会引起大量的区间更新、合并操作。显然这也是不明智的选择。

因此，我们想要寻找一种折中的方案，使得区间求和和单点修改的时间复杂度都不会太大。那么我们需要考虑引起时间开销的原因：

对于单点修改，在前缀和下需要对区间进行更新操作；对于区间求和，在朴素算法下需要对区间内的子区间进行合并操作。

那么我们能否找到这样一种结构：单点修改时引发的区间更新数量不会太多、区间查询时需要进行合并的对象不会太多，那么这就需要引出我们本篇文章的主要对象：树状数组(BIT)。

2.简介

树状数组(Binary Indexed Tree)又称二叉搜索树，简称BIT。

树状数组是这样一种数据结构：在$O(\log n)$时间复杂度下，支持单点修改、区间查询的一种储存结构。

对于树状数组，我们很容易联系到线段树：线段树支持单点修改、区间修改、区间查询。同时在$Lazy$标记的辅助下，能够实现很优秀的区间修改算法。如下是一棵线段树的结构：

但是在许多场景下，我们并不要进行区间修改，仅仅是进行简单的单点修改和区间查询，因此我们可以引入树状数组。与线段树相比，树状数组的代码更为简洁，在解决一类问题(单点修改)时具有突出的优势。如下是一个树状数组的结构示意图：

我们通过这张图对树状数组的结构进行分析，并介绍具体的原理。

这里可能会引发一个疑问：上图实际上并不是一棵二叉树？

我们通过一个动画来解释这个问题：

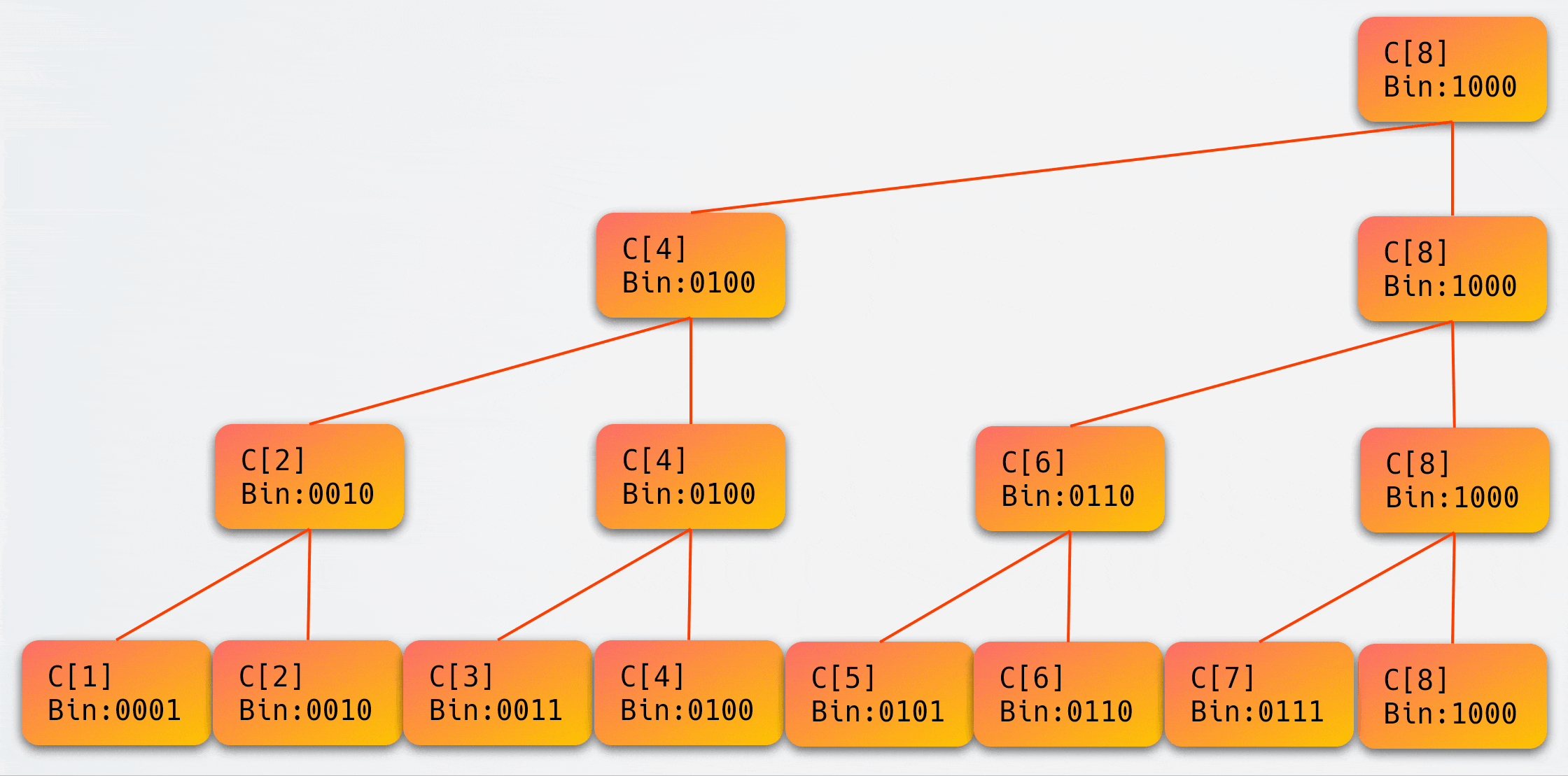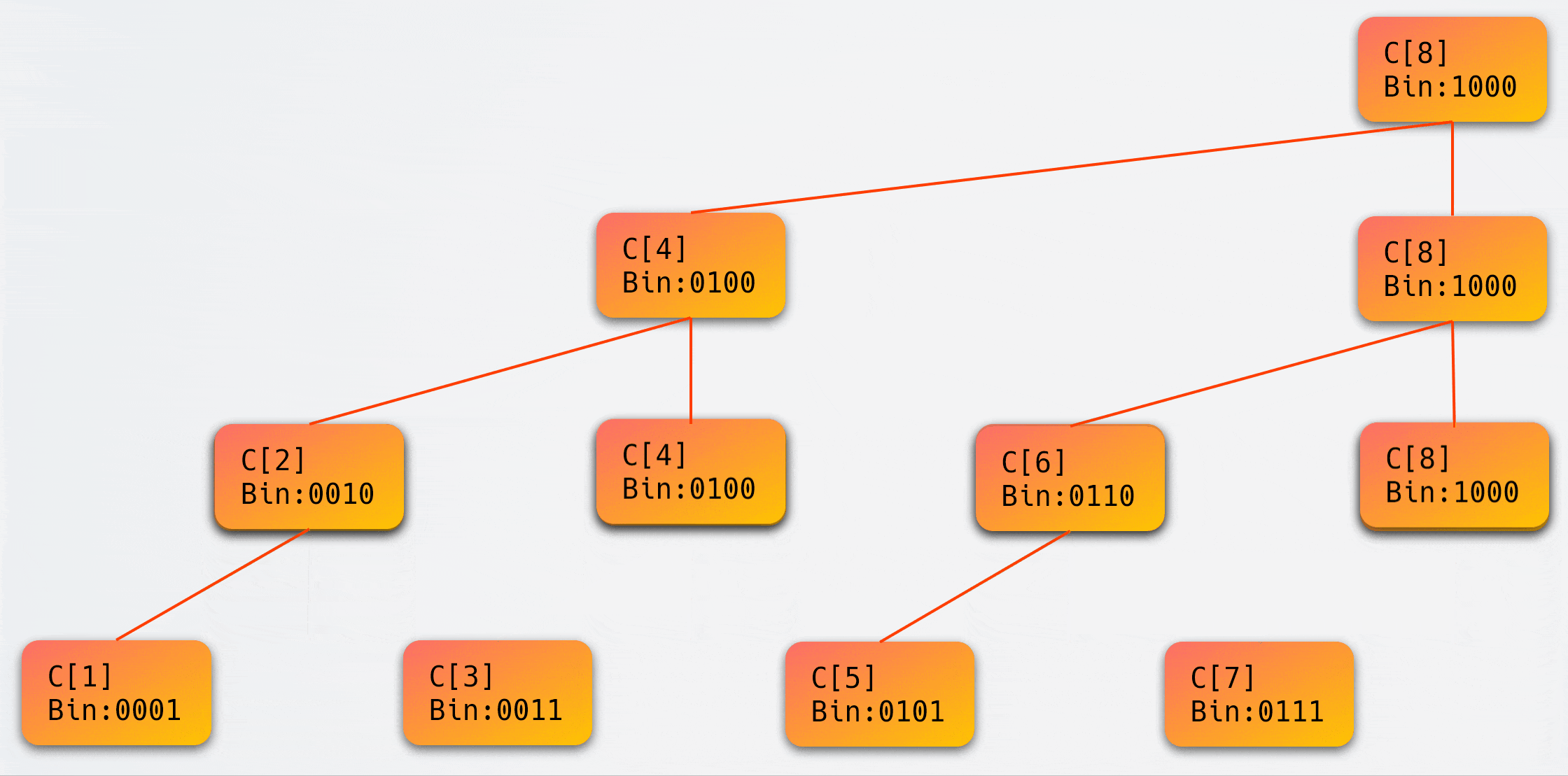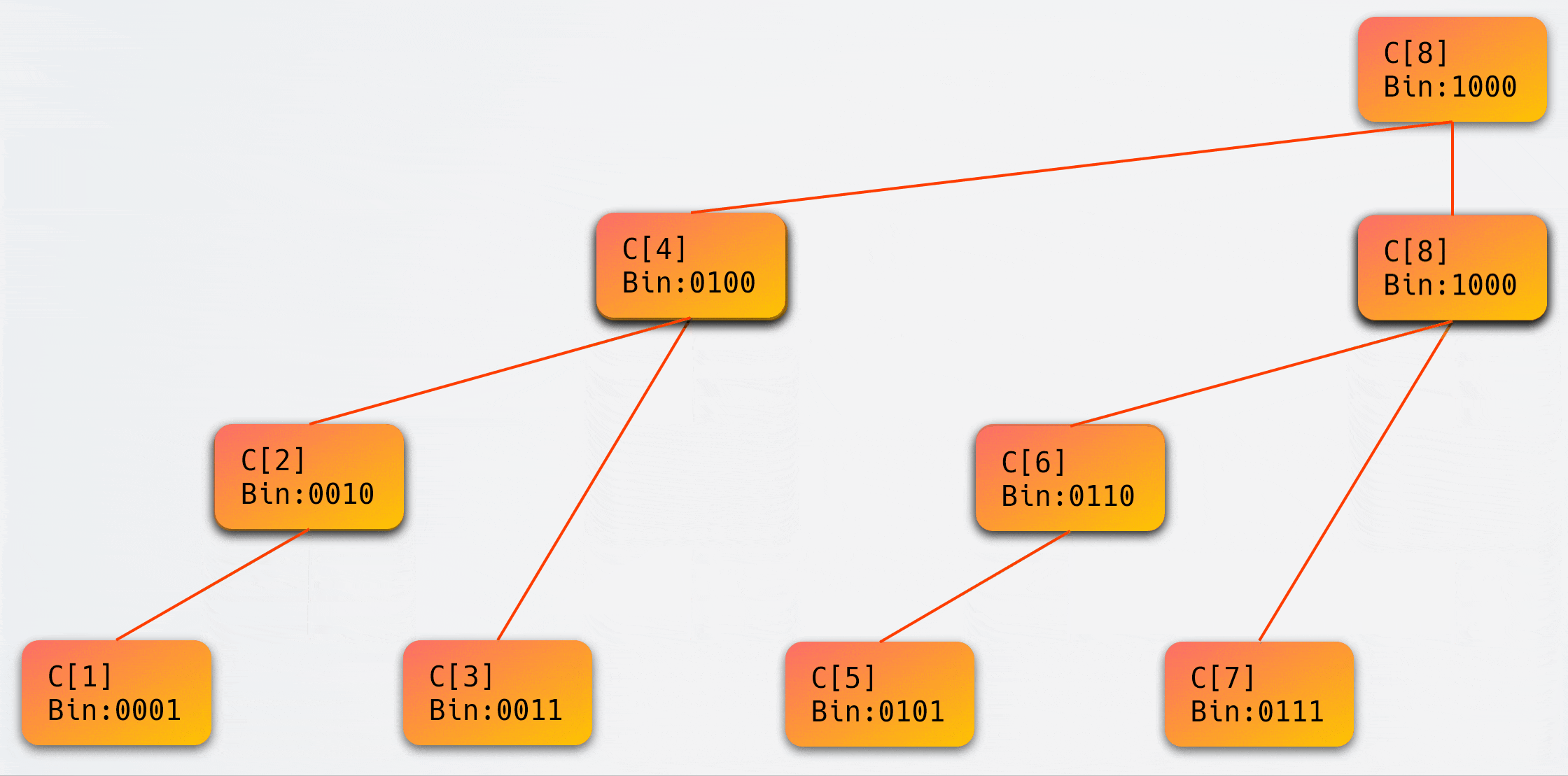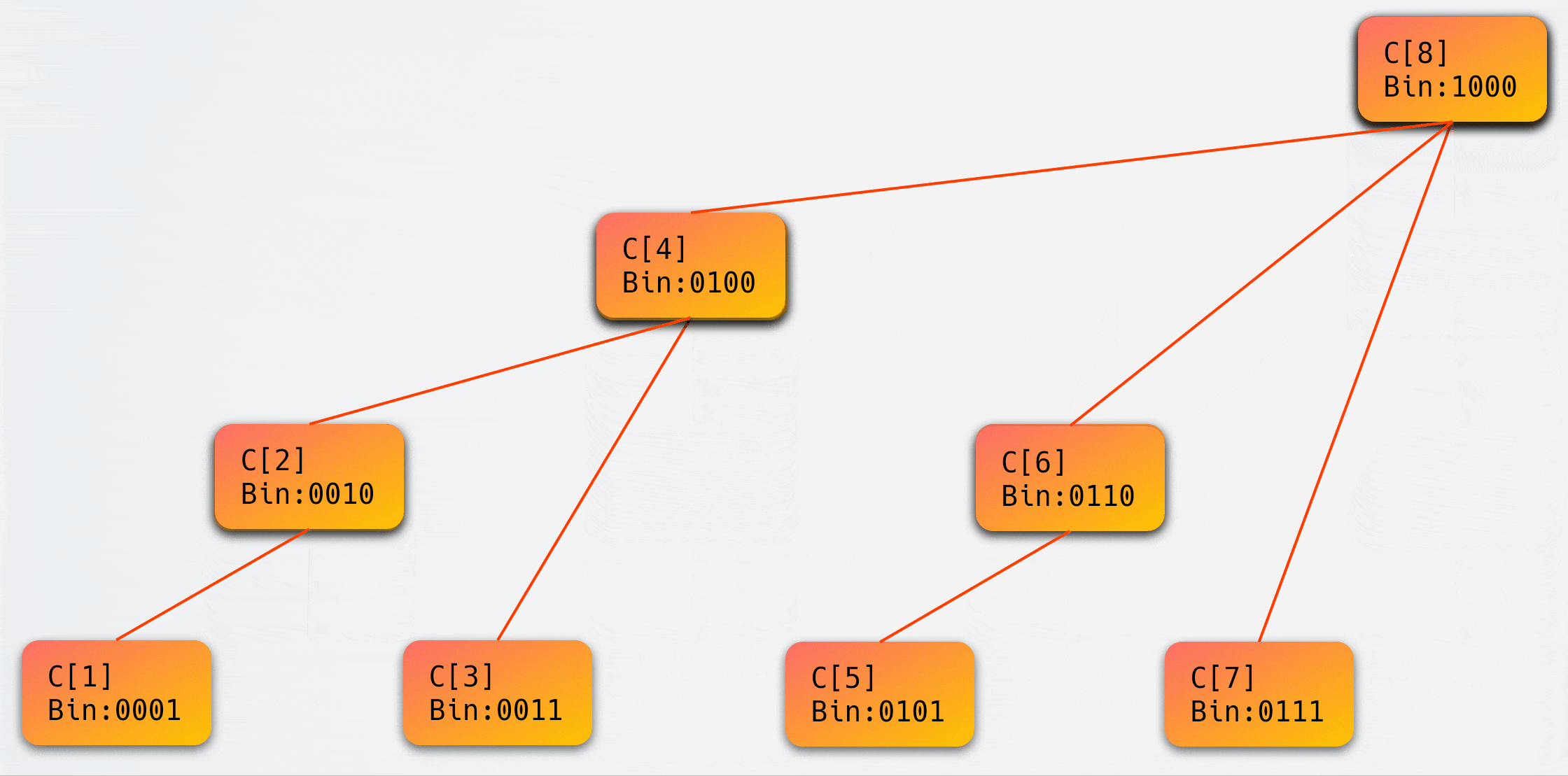
二、树状数组 详解

1.区间查询 详解

首先，我们给出一个长度为$8$的数组(为了计算方便，我们约定下标从$1$开始)。其树状数组结构如下图所示：

现在我们复现一下一开始提出的问题，单点修改，区间求和。

如果我们要求前$8$项的和，那么我们需要查询的区间是$((0000)_2,(1000)_2]$；

如果我们要求前7项的和，那么我们需要查询的区间是$((0000)_2,(0100)_2],((0100)_2, (0110)_2],((0110)_2, (0111)_2]$;

$...$

查询的区间是如何得到的？区间右端点不断地取最低为$1$的位并改为$0$，作为左端点，直到没有$1$(即为$0$)时结束。

我们再学习状态压缩的时候曾经使用过这样一个函数$lowbit(x)$，它的作用是返回$x$二进制表示中最低位为$0$的数。

#define

这么做的依据是什么？我们回到结构图中，很显然可以看出：
$c_2$ 管理的对象是 $a_1$&$a_2$；
$c_4$ 管理的对象是 $a_1$&$a_2$&$a_3$&$a_4$；
$c_6$ 管理的对象是 $a_5$&$a_6$；
$c_8$ 则管理全部 $8$

如果我们要求前$7$项的和，我们从$c_7$开始，$c_7$只管理一个点$a_7$；继续向前找会找到$c_6$，而$c_6$管理 $a_5$&$a_6$；那么我们跳过被管理的元素继续向前找会找到$c_4$，管理的是 $a_1$&$a_2$&$a_3$&$a_4$。那么显然，查询操作结束。不难发现：查询的过程被不停的压缩优化。

那么我们只需要通过$c_i$维护区间$(a_i - lowbit(a_i), a_i]$，这样在查询前合并的区间数是小于$\log_2 n$的。我们将$a$数组和$c$数组的对应关系用结构图进行说明：

2.单点修改 详解

解决了区间查询的问题，我们来解决单点修改的问题。如何维护树状数组$c$呢？

假如我们要对$A[5]$进行修改，那么我们从$c_5$出发，沿着$c_5 \rightarrow c_6 \rightarrow c_8$的路径进行修改。这条路径是怎样得到的？

我们将下标二进制化，再来观察路径：$c[0101] \rightarrow c[0110] \rightarrow c[1000]$，不难发现：更新路径上相邻结点$c_i$ 和 $c_{i + 1}$ 刚好相差一个$lowbit(i)$，那么更新的过程就很简单了，循环取$lowbit(i)$更新$c_i、c_{i + lowbit(i)}...$直到$i = MAXN$ ($MAXN$为数组长度)。

这样，我们就得到了一种可以在$O(\log n)$时间下支持单点修改和区间查询的数据结构。

3.两种操作的具体实现

经过上述分析，我们可以对两种操作进行实现：

#define
#define
int a[MAXN], len;
int tree[MAXN];
//树状数组初始化(O(n)建树)
inline void init(){
    memset(tree, 0, sizeof(tree));
    for(int i = 1, tmp = 0; i <= len; i++){
        tree[i] = a[i];
        tmp = i + lowbit(i);
        if(tmp <= n) tree[tmp] += tree[i];
    }
}
//单点修改-更新路径
inline void update(int i, int x){
    for(int pos = i; pos <= len; pos += lowbit(pos)) tree[pos] += x;
}
//求前n项和
inline int getsum(int i){
    int ans = 0;
    for(int pos = i; pos; pos -= lowbit(pos)) ans += tree[pos];
    return ans;
}
//区间查询
inline int query(int l ,int r){
    return getsum(b) - getsum(a - 1);
}

不难发现，几种操作都十分简单(相比于线段树)，因此树状数组在解决单纯的“单点修改+区间查询”问题时是非常优秀的数据结构。

三、树状数组 总结

1.树状数组 - 区间加 区间求和

在上述的操作中，我们对于区间求和的过程是基于朴素求和得到的，如果仅仅针对区间加和区间求和这一种应用方式，我们可以通过前缀和与差分对这一过程继续进行优化：

若维护序列 $a$ 的差分数组 $b$，此时我们对 $a$ 的一个前缀 $r$ 求和，即 $\sum_{i=1}^{r} a_i$，由差分数组定义得 $a_i=\sum_{j=1}^i b_j$

进行推导

$\begin{aligned} &\sum_{i=1}^{r} a_i\\=&\sum_{i=1}^r\sum_{j=1}^i b_j\\=&\sum_{i=1}^r b_i\times(r-i+1) \\=&\sum_{i=1}^r b_i\times (r+1)-\sum_{i=1}^r b_i\times i \end{aligned}$

区间和可以用两个前缀和相减得到，因此只需要用两个树状数组分别维护 $\sum b_i$ 和 $\sum i \times b_i$，就能实现区间求和。

#define
#define
int tree1[MAXN], tree2[MAXN], a[MAXN], len;
//建树，这里不用0(n)建树
inline void init(){
    for(int i = 1; i <= len; i++) update(i, a[i]), update(i + 1， -x);
}
//对两个树状数组进行更新
inline void add(int i, int x){
    int x1 = i * x;
    for(int pos = i; pos <= len; pos += lowbit(pos)) tree1[pos] += x, tree2[pos] += x1;
}
//将区间加差分为两个前缀和
inline void update(int l, int r, int x){
    add(l, x), add(r + 1, -x);
}
//对指定的树状数组求前n项和
inline int getsum(int *tree, int i){
    int sum = 0;
    for(int pos = i; pos; pos -= lowbit(pos)) ans += tree[i];
    return sum;
}
//区间和查询
inline int query(int l, int r){
    return (r + 1) * getsum(t1, r) - l * getsum(t1, l - 1) - (getsum(t2, r) - getsum(t2, l - 1));
}

2.树状数组 - $O(\log n)$查询第$k$小/大元素

在此以第$k$小的元素为例。若求第$k$大则可以通过简单计算进行转化。

我们需要再次借用线段树中的思想。我们在可持久化线段树中，在求区间第$k$小时，将所有数字看成一个可重集合，即定义数组 $a$ 表示值为 $i$ 的元素在整个序列重出现了 $a_i$ 次。找第 $k$ 大就是找到最小的 $x$ 恰好满足 $\sum_{i=1}^{x}a_i \geq k$

因此可以想到算法：如果已经找到 $x$ 满足 $\sum_{i=1}^{x}a_i \le k$，考虑能不能让 $x$ 继续增加，使其仍然满足这个条件。找到最大的 $x$ 后，$x+1$ 就是所要的值。
在树状数组中，节点是根据 2 的幂划分的，每次可以扩大 2 的幂的长度。令 $sum$ 表示当前的 $x$ 所代表的前缀和，有如下算法找到最大的 $x$：

1. 求出$depth=\left \lfloor \log_2n \right \rfloor$
2. 计算$t=\sum_{i=x+1}^{x+2^{depth}}a_i$
3. 如果$sum+t \le k$，则此时扩展成功，将$2^{depth}$累加到$x$上；否则扩展失败，对$x$
4. 将$depth$减 1，回到步骤 2，直至$depth$

int kth(int i){
    int cnt = 0, ret = 0;
    for (int i = log2(len); ~i; --i){                           // i与上文depth含义相同
        ret += 1 << i;                                          // 尝试扩展
        if (ret >= len || cnt + tree[ret] >= i)  ret -= 1 << i; //扩展失败
        else cnt += tree[ret]; // 扩展成功后 要更新之前求和的值
    }
    return ret + 1;
}

3.时间戳优化

时间戳优化有什么用？

我们经常碰到多组输入的题目，按照一般操作，每次输入新数据后我们会$memset$暴力清空数组。但如果每次输入新数据时，都暴力清空树状数组，就可能会造成超时。

因此使用 $tag$ 标记，存储当前节点上次使用时间（即最近一次是被第几组数据使用）。每次操作时判断这个位置 $tag$

#define
#define
int tag[MAXN], t[MAXN], Tag, len;
void reset() { ++Tag; }
void update(int k, int v){
    while (k <= len){
        if (tag[k] != Tag) t[k] = 0;
        t[k] += v, tag[k] = Tag;
        k += lowbit(k);
    }
}
int getsum(int k){
    int ret = 0;
    while (k){
        if (tag[k] == Tag) ret += t[k];
        k -= lowbit(k);
    }
    return ret;
}
t[k] = 0;
        t[k] += v, tag[k] = Tag;
        k += lowbit(k);
    }
}
int getsum(int k){
    int ret = 0;
    while (k){
        if (tag[k] == Tag) ret += t[k];
        k -= lowbit(k);
    }
    return ret;
}