【leetcode-数组】杨辉三角 II

题目：

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

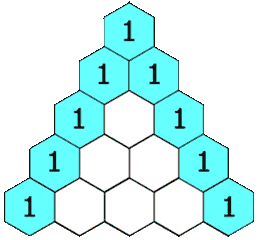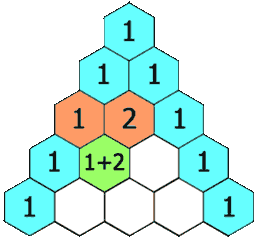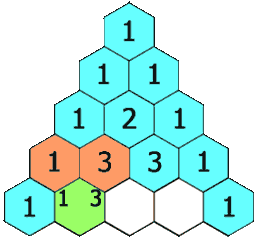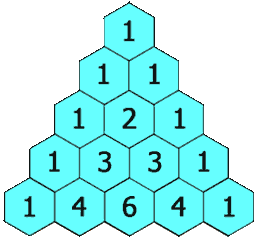
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3

输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

---

思路：

观察发现。二维数组的值可分为两种情况：边界值为1，中间值 由左上加上右上。题目k的取值范围[0,33], 所以先求出行数为k+1的二维矩阵，即[0, 1, 2, ..., k] ，再返回第k行即可。

java代码：

class Solution {
     public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> res = new ArrayList<>();

        List<Integer> res0 = new ArrayList<>();
        res0.add(1);
        res.add(res0);

        for (int i = 1; i <= rowIndex; i++) {
            List<Integer> one = new ArrayList<>();
            one.add(1);
            for (int j = 1; j < i; j++) {
                List<Integer> pre = res.get(i - 1);

                one.add(pre.get(j - 1) + pre.get(j));
            }
            one.add(1);

            res.add(one);
        }

        return res.get(rowIndex);

    }
}

 

由于水平有限，文章中难免会有一些错误，有纰漏之处恳请各位大佬不吝赐教！

及时更新最新文章和学习资料，一起来学习：