文接上文,我们继续计算几何内容的整理和知识体系的构建,本来计划本次更新最小外包矩形的内容,但是在看书看视频的过程中,我发现有一些基础算法内容需要介绍,所以本文我们来介绍在空间几何算法中比较基础的几个算法:
- 点在有向线段的两侧判断
- 点集组成的环方向判断
- 点在面判断,是否在面内
- 点到线段的最短距离以及最短点
以上几个算法,在一般业务中没有应用的场景,但是在空间算法中有着举足轻重的地位,是大部分算法的基础。
1. 点在有向线段的两侧判断
1.1. 线性规划思路
已知P(0,0),Q(3,2)两点,试判断P,Q是否在直线2x+3y=4的同一侧。
//直线
2x+3y=4
//即直线
2x+3y-4=0
//把P、Q代入
//2x+3y-4得到
2*0+3*0-4=-4<0
2*3+3*2-4=8所以在两侧!!!
1.2. 向量思路
我们设定线段PQ为线段,A为测试点。则我们可以使用向量叉积来进行判断
两个向量内积等于零,则它们正交(垂直)。
- 内积的表达方式为:
=
=
*CosAB
两个向量的叉积等于零,则它们平行。
- 叉积(外积)的表达方式为:
=
=
*SinAB
叉积的一个非常重要性质是可以通过它的符号判断两矢量相互之间的顺逆时针关系:
- 若
> 0 , 则点A向量
的顺时针方向。
- 若
< 0 , 则点A向量
的逆时针方向。
- 若
= 0 ,
则P与Q共线,但可能同向也可能反向。
1.3. 向量积思路
定义:平面上的三点P1(x1,y1),P2(x2,y2),P3(x3,y3)的面积量:
S(P1,P2,P3)=|y1 y2 y3|= (x1-x3)*(y2-y3)-(y1-y3)*(x2-x3)当P1P2P3逆时针时S为正的,当P1P2P3顺时针时S为负的。
令矢量的起点为A,终点为B,判断的点为C,
- 如果S(A,B,C)为正数,则C在矢量AB的左侧;
- 如果S(A,B,C)为负数,则C在矢量AB的右侧;
- 如果S(A,B,C)为0,则C在直线AB上。
2. 点集组成的环方向判断
OGC关于数据格式有规定,多边形的外环应为逆时针,内环应为顺时针。GIS相关的库包,在对数据进行空间操作的时候,也基于这个规定,将数据标准化为外环逆时针,内环顺时针之后,再进行空间计算和分析。
如果结果S大于0,说明是逆时针,如果结果S小于0,说明是顺时针。
3. 点在面判断,是否在面内
3.1 射线法
http://alienryderflex.com/polygon/
解法:从这个点做一条射线,计算它跟多边形边界的交点个数,如果交点个数为奇数,那么点在多边形内部,否则点在多边形外。
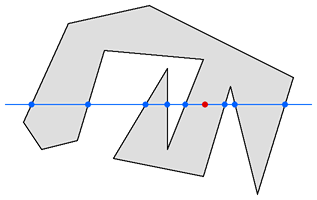
3.2 回转数法
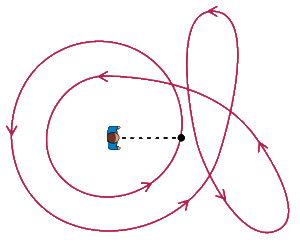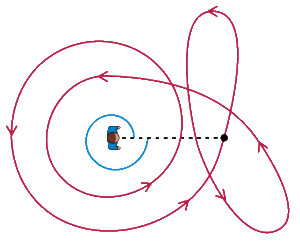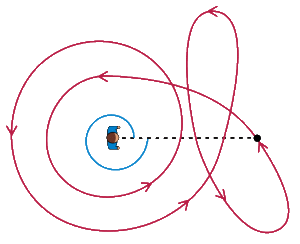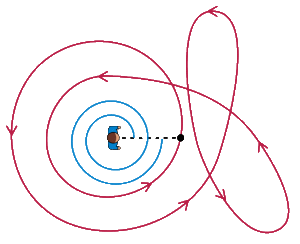
解法:面中的闭合曲线关于一个点的回转数(又叫卷绕数),代表了曲线绕过该点的总次数。下面这张图动态演示了回转数的概念:图中红色曲线关于点(人所在位置)的回转数为 2。
结论:角度和为360度,所以a在多边形内,反之,如果角度和小于360度,则不在
/**
* @description 回转数法判断点是否在多边形内部
* @param {Object} p 待判断的点,格式:{ x: X坐标, y: Y坐标 }
* @param {Array} poly 多边形顶点,数组成员的格式同 p
* @return {String} 点 p 和多边形 poly 的几何关系
*/
function windingNumber(p, poly) {
var px = p.x,
py = p.y,
sum = 0
for(var i = 0, l = poly.length, j = l - 1; i < l; j = i, i++) {
var sx = poly[i].x,
sy = poly[i].y,
tx = poly[j].x,
ty = poly[j].y
// 点与多边形顶点重合或在多边形的边上
if((sx - px) * (px - tx) >= 0 && (sy - py) * (py - ty) >= 0 && (px - sx) * (ty - sy) === (py - sy) * (tx - sx)) {
return 'on'
}
// 点与相邻顶点连线的夹角
var angle = Math.atan2(sy - py, sx - px) - Math.atan2(ty - py, tx - px)
// 确保夹角不超出取值范围(-π 到 π)
if(angle >= Math.PI) {
angle = angle - Math.PI * 2
} else if(angle <= -Math.PI) {
angle = angle + Math.PI * 2
}
sum += angle
}
// 计算回转数并判断点和多边形的几何关系
return Math.round(sum / Math.PI) === 0 ? 'out' : 'in'
}回转数是拓扑学中的一个基本概念,具有很重要的性质和用途。
- 点在面内

- 点在面外

4. 点到线段的最短距离以及最短点

double PointToSegDist(double x, double y, double x1, double y1, double x2, double y2)
{
double cross = (x2 - x1) * (x - x1) + (y2 - y1) * (y - y1);
if (cross <= 0) return Math.Sqrt((x - x1) * (x - x1) + (y - y1) * (y - y1));
double d2 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
if (cross >= d2) return Math.Sqrt((x - x2) * (x - x2) + (y - y2) * (y - y2));
double r = cross / d2;
double px = x1 + (x2 - x1) * r;
double py = y1 + (y2 - y1) * r;
return Math.Sqrt((x - px) * (x - px) + (py - y) * (py - y));
}
r = cross / d2;
double px = x1 + (x2 - x1) * r;
double py = y1 + (y2 - y1) * r;
return Math.Sqrt((x - px) * (x - px) + (py - y) * (py - y));
}





















