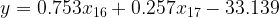回归分析的基本思想是: 虽然自变量和因变量之间没有严格的、确定性的函数关系,但可以设法找出最能代表它们之间关系的数学表达形式。
多元回归分析的由来: 在自变量很多时,其中有的因素可能对应变量的影响不是很大,而且x之间可能不完全相互独立的,可能有种种互相作用的关系。 在这种情况下可用逐步回归分析,进行x因子的筛选,这样建立的多元回归模型预测效果会更好。
逐步回归法:逐步回归的基本思想是将变量逐个引入模型,每引入一个解释变量后都要进行F检验,并对已经选入的解释变量逐个进行t检验,当原来引入的解释变量由于后面解释变量的引入变得不再显著时,则将其删除。以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程,直到既没有显著的解释变量选入回归方程,也没有不显著的解释变量从回归方程中剔除为止。以保证最后所得到的解释变量集是最优的。
依据上述思想,可利用逐步回归筛选并剔除引起多重共线性的变量。
其具体步骤如下:

可以解决的实际问题:
- 收入水平与受教育程度、所在行业、工作 年限、工作种类的关系。
- 公路客运量与人口增长量、私家车保有量、 国民生产总值、国民收入、工农业总产值、 基本建设投资额、城乡居民储蓄额、铁路 和水运客运量等因素的关系。
Q:以陕西省长武地区1984~1995年的烟蚜传毒病情资料、相关虫情和气象资料为例, 建立蚜传病毒病情指数的逐步回归模型, 说明逐步回归分析的具体步骤。影响蚜传病毒病情指数的虫情因子和气象因子一共有21个,通过逐步回归,从中选出对病情指数影响显著的因子,从而建立相应的模型。

以excel文件的形式导入spss
此时的年份作为label,x1作为因变量,其他因素作为自变量(按住shift同时拉入多个因素)。
【分析】-【回归】-【线性】-【方法】步进【选项】设置F-enter and F-remove-【输出】
输入/除去的变量a | |||
模型 | 输入的变量 | 除去的变量 | 方法 |
1 | x16 | . | 步进(条件:要输入的 F 的概率 <= .150,要除去的 F 的概率 >= .200)。 |
2 | x17 | . | 步进(条件:要输入的 F 的概率 <= .150,要除去的 F 的概率 >= .200)。 |
a. 因变量:x1 |
模型摘要c | |||||
模型 | R | R 方 | 调整后 R 方 | 标准估算的错误 | 德宾-沃森 |
1 | .762a | .581 | .539 | 22.08153 |
|
2 | .844b | .713 | .649 | 19.26609 | 2.313 |
a. 预测变量:(常量), x16 |
b. 预测变量:(常量), x16, x17 |
c. 因变量:x1 |
ANOVAa | ||||||
模型 | 平方和 | 自由度 | 均方 | F | 显著性 | |
1 | 回归 | 6760.381 | 1 | 6760.381 | 13.865 | .004b |
残差 | 4875.941 | 10 | 487.594 |
|
| |
总计 | 11636.322 | 11 |
|
|
| |
2 | 回归 | 8295.681 | 2 | 4147.841 | 11.175 | .004c |
残差 | 3340.641 | 9 | 371.182 |
|
| |
总计 | 11636.322 | 11 |
|
|
| |
a. 因变量:x1 |
b. 预测变量:(常量), x16 |
c. 预测变量:(常量), x16, x17 |
此时的两个模型则分别是对应x16以及x16、x17为变量的线性回归方程。
系数a | ||||||
模型 | 未标准化系数 | 标准化系数 | t | 显著性 | ||
B | 标准错误 | Beta | ||||
1 | (常量) | -16.055 | 9.917 |
| -1.619 | .137 |
x16 | .985 | .265 | .762 | 3.724 | .004 | |
2 | (常量) | -33.139 | 12.059 |
| -2.748 | .023 |
x16 | .753 | .257 | .583 | 2.924 | .017 | |
x17 | .257 | .126 | .405 | 2.034 | .072 | |
a. 因变量:x1 |
第一步对x16做简单线性回归:y = 0.985x16-16.005
第二步对x16、x17做线性回归:y = 0.753x16+0.257x17-33.139
排除的变量a | ||||||
模型 | 输入 Beta | t | 显著性 | 偏相关 | 共线性统计 | |
容差 | ||||||
1 | x2 | -.132b | -.584 | .573 | -.191 | .881 |
x3 | -.028b | -.127 | .902 | -.042 | .942 | |
x4 | -.027b | -.125 | .903 | -.042 | .997 | |
x5 | -.050b | -.203 | .844 | -.068 | .751 | |
x6 | .024b | .113 | .913 | .038 | .999 | |
x7 | -.033b | -.133 | .897 | -.044 | .744 | |
x8 | .213b | 1.037 | .327 | .327 | .985 | |
x9 | -.030b | -.132 | .898 | -.044 | .901 | |
x10 | .130b | .609 | .558 | .199 | .979 | |
x11 | .200b | .953 | .365 | .303 | .957 | |
x12 | -.121b | -.560 | .589 | -.183 | .963 | |
x13 | .095b | .438 | .672 | .144 | .978 | |
x14 | .225b | 1.020 | .334 | .322 | .856 | |
x15 | -.137b | -.648 | .533 | -.211 | .992 | |
x17 | .405b | 2.034 | .072 | .561 | .803 | |
x18 | .302b | 1.192 | .264 | .369 | .626 | |
x19 | -.327b | -1.754 | .113 | -.505 | .999 | |
x20 | -.132b | -.623 | .549 | -.203 | .988 | |
x21 | -.353b | -1.632 | .137 | -.478 | .769 | |
2 | x2 | -.085c | -.422 | .684 | -.148 | .868 |
x3 | -.038c | -.197 | .849 | -.069 | .941 | |
x4 | -.103c | -.544 | .601 | -.189 | .958 | |
x5 | -.026c | -.119 | .909 | -.042 | .749 | |
x6 | .006c | .030 | .976 | .011 | .996 | |
x7 | .059c | .265 | .798 | .093 | .710 | |
x8 | .238c | 1.383 | .204 | .439 | .981 | |
x9 | -.094c | -.473 | .649 | -.165 | .877 | |
x10 | .225c | 1.252 | .246 | .405 | .928 | |
x11 | .184c | 1.007 | .344 | .335 | .955 | |
x12 | .016c | .076 | .941 | .027 | .836 | |
x13 | .080c | .424 | .683 | .148 | .976 | |
x14 | .067c | .294 | .776 | .103 | .693 | |
x15 | -.139c | -.754 | .473 | -.257 | .992 | |
x18 | .231c | 1.010 | .342 | .336 | .608 | |
x19 | -.168c | -.728 | .487 | -.249 | .631 | |
x20 | .007c | .032 | .975 | .011 | .847 | |
x21 | -.230c | -1.056 | .322 | -.350 | .662 | |
a. 因变量:x1 |
b. 模型中的预测变量:(常量), x16 |
c. 模型中的预测变量:(常量), x16, x17 |
残差统计a | |||||
| 最小值 | 最大值 | 平均值 | 标准偏差 | 个案数 |
预测值 | -13.3111 | 85.9252 | 12.2325 | 27.46184 | 12 |
残差 | -31.99095 | 28.60478 | .00000 | 17.42684 | 12 |
标准预测值 | -.930 | 2.683 | .000 | 1.000 | 12 |
标准残差 | -1.660 | 1.485 | .000 | .905 | 12 |
a. 因变量:x1 |
最终得出: