自回归算法 java 自回归算法 c语言实现

今天我们用C语言实现一个简单的线性回归算法；在代码前面我们在回顾一下线性回归。

线性回归是回归问题中的一种，线性回归假设目标值与特征是线性相关的，即满足一个多元一次方程式。通过构建损失函数，来求解损失函数最小时的参数W和b。通常表达式可以表示如下：

                                                                      

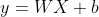
其中 y 为预测值，自变量X和因变量y是已知的，我们要想实现的是，当一个新增的X出现时，我们要预测y的值。因此我们构建这个函数关系，是通过已知的数据求解函数模型中位置的W和b这两个参数。

     我们用均方误差为损失函数即：

将函数带入即为：

我们现在的任务就是求解最小化  L 时的W 和b，即将核心目标优化为

 

此处我们用梯度下降法进行求解

为了求偏导数，当只有一个样本时，即： 

我们这里就简单的处理为求解，至于计算何时结束我们先不做考虑，就简单粗暴给其设定计算次数。

理解了最小误差的求解原理我们就开始上代码了。

 

LinerRegression.h

#ifndef LINERREGRESSION_LINERREGRESSION_H
#define LINERREGRESSION_LINERREGRESSION_H

//初始化函数

void set_config(double learning_rate,long int max_iter,int X_Len);
//训练
void fit(double *train_x,double *train_y);
//计算

double* _f(const double *train_x,double w,double b);

//预测
double* predict(double *train_x);
//损失

double loss(const double *y_true,const double *y_pred);
//求梯度

void _calc_gradient();
//单步更新
void _train_step();

#endif

LinerRegression.c

#include <stdio.h>
#include <stddef.h>
#include <malloc.h>
#include "LinerRegression.h"


//设置固定学习率
double g_learning_rate = 0.01;
//设置梯度更新次数
long int g_max_iter = 100;
//设置初始化 W
double g_w = 5;
//设置初始化 b
double g_b = 5;
//定义保存损失的指针
double *loss_arr_pt;
//定义保存时时计算y的指针
double *g_out_Y_pt;
//定义保存时时预测y的指针
double *y_pred_pt;

//输入 X 
double *X_pt;
//输入 Y
double *Y_pt;
//训练数据长度
int g_X_Len;

//更新 梯度
double d_w;
double d_b;

double loss_val[1];

void set_config(double learning_rate, long int max_iter, int X_Len) {
    g_learning_rate = learning_rate;
    g_max_iter = max_iter;
//    g_w = gaussrand();
//    g_b = gaussrand();
    g_X_Len = X_Len;
    loss_arr_pt = malloc((size_t) max_iter);
    g_out_Y_pt = malloc((size_t) X_Len);
    y_pred_pt = malloc((size_t) X_Len);
}


void fit(double *train_x, double *train_y) {
    X_pt = train_x;
    Y_pt = train_y;
    for (int i = 0; i < g_max_iter; ++i) {
        printf("step %d: ", i);
        _train_step();
        loss(NULL, NULL);
        loss_arr_pt[i] = loss_val[0];
    }
}

double *_f(const double *train_x, double w, double b) {
    for (int i = 0; i < g_X_Len; i++) {
        //y = w * x + b
        g_out_Y_pt[i] = train_x[i] * w + b;
    }
    return g_out_Y_pt;
}

//预测
double *predict(double *train_x) {
    if (train_x == NULL) {
        train_x = X_pt;
    }
    y_pred_pt = _f(train_x, g_w, g_b);
    return y_pred_pt;
}

//计算损失
double loss(const double *y_true, const double *y_pred) {
    if (y_true == NULL || y_pred == NULL) {
        y_true = Y_pt;
        y_pred = predict(X_pt);
    }
    double loss_total = 0;
    for (int i = 0; i < g_X_Len; i++) {
        loss_total += (y_true[i] - y_pred[i]) * (y_true[i] - y_pred[i]);
    }
    loss_val[0] = loss_total / g_X_Len;
    return loss_val[0];
}

//求梯度
void _calc_gradient() {
    double d_w_total = 0;
    double d_b_total = 0;
    for (int i = 0; i < g_X_Len; i++) {
        //迭代计算梯度
        d_w_total += ((X_pt[i] * g_w + g_b - Y_pt[i]) * X_pt[i]);
        d_b_total += (X_pt[i] * g_w + g_b - Y_pt[i]);
    }
    d_w = d_w_total / g_X_Len;
    d_b = d_b_total / g_X_Len;
}

//更新 W 和 b
void _train_step() {
    _calc_gradient();
    //更新 W和b
    g_w = g_w - g_learning_rate * d_w;
    g_b = g_b - g_learning_rate * d_b;

    //输出时时 W 和b 以及损失
    printf(" g_w = %f,", g_w);
    printf("g_b = %f,", g_b);
    printf(" loss = %f\n", loss_val[0]);

}

 

main.c

#include "utils/util.h"

#include "src/MultipleLinearRegression.h"
#include "src/LinerRegression.h"

int main() {
    //指定学习率
    double learning_rate = 0.01;
    //指定梯度下降计算次数
    int iteration_count = 2000;

    //生成输入变量的参数k、b; y = kx + b
    double k = 20.0;
    double b = 15;

    //训练数据大小
    int data_size = 100;
    int train_size = 70;
    int test_size = 30;

    double temp_rand[data_size];
    double X_data[data_size];
    double Y_data[data_size];
    double train_X[train_size];
    double train_Y[train_size];
    double test_X[test_size];
    double test_Y[test_size];
    //随机获取 输入变量X
    getRand(X_data, data_size);
    for (int i = 0; i < data_size; ++i) {
        getRand(temp_rand, data_size);
        Y_data[i] = k * X_data[i] + b + temp_rand[i] / 10;
    }
    for (int j = 0; j < data_size; ++j) {
        if (j < train_size) {
            train_X[j] = X_data[j];
            train_Y[j] = Y_data[j];
        } else {
            test_X[j - train_size] = X_data[j];
            test_Y[j - train_size] = Y_data[j];
        }
    }

    set_config(learning_rate, iteration_count, train_size);
    fit(train_X, train_Y);

其中用到生成随机输入变量方法如下：

int* getRand(double *a,int len){
    int i;
    srand(time(NULL));//设置当前时间为种子
    for (i = 0; i < len; ++i){
        a[i] = rand()%10+1;//产生1~10的随机数
    }
    return a;
}

可以看到在计算1000之后 W　和　ｂ已经很接近我们初时设置的值了：

step 989:  g_w = 20.235078,g_b = 14.003770, loss = 0.210872
step 990:  g_w = 20.234798,g_b = 14.005839, loss = 0.209997
step 991:  g_w = 20.234518,g_b = 14.007905, loss = 0.209125
step 992:  g_w = 20.234238,g_b = 14.009966, loss = 0.208257
step 993:  g_w = 20.233959,g_b = 14.012023, loss = 0.207393
step 994:  g_w = 20.233681,g_b = 14.014076, loss = 0.206532
step 995:  g_w = 20.233403,g_b = 14.016124, loss = 0.205674
step 996:  g_w = 20.233126,g_b = 14.018169, loss = 0.204821
step 997:  g_w = 20.232849,g_b = 14.020209, loss = 0.203970
step 998:  g_w = 20.232573,g_b = 14.022244, loss = 0.203124
step 999:  g_w = 20.232298,g_b = 14.024276, loss = 0.202281

 

至此我们简单的一元线性回归就这样实现了。至于学习率更优雅的指定和学习停止条件我们后面再讨论。