线性规划:
线性规划在matlab中的标准形式:
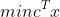

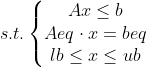
其中c和x为n维向量,A、Aeq为适当维数的列向量。
[x,fval]=linprog(c,A,b,Aeq,beq,LB,UB,X0,OPTIONS)favl返回目标函数的值,LB和UB分别为变量
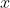
的下界和上界,
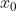
是
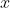
的初始值,OPTIONS是控制参数。
一、运输问题
(产销平衡,运费最省)
某商品有
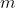
个产地、
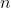
个销地,各产地的产量分别为

,各销地的 需求量分别为
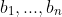
。若该商品由
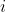
产地运到

销地的单位运价为
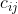
,问应该如何调运才能使总运费最省?引入变量
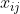
,其取值为由i产地运往
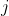
销地的该商品数量。数学模型为:
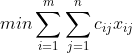
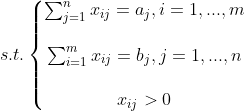
可直接用标准法求解。
对于产销平衡的运输问题,有关系:
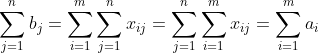
因约束矩阵比较特殊,可用表上作业法。
二、指派问题
拟分配
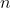
人去干
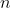
项工作,每人干且仅干一项工作,若分配第

人去干第
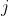
项工作,需花费
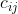
单位时间,问应如何分配工作才能使工人花费的总时间最少?引入变量

,若分配
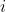
干

工作,则取
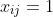
,否则取
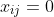
。数学模型为:
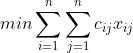

因最终为0-1矩阵,可用匈牙利算法求解。
链接中变换矩阵后为:

(不过最终更新的矩阵为:)

从变换后的矩阵就已经可以看出最优指派矩阵了(独立0元素):
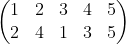
即,
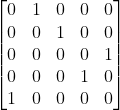
带入最初的矩阵,即:

就可求出:
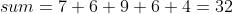
三、对偶理论
原始问题:

对偶问题:
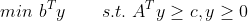
基本性质:
- 对称性:对偶问题的对偶是原问题。
- 弱对偶性:若是原问题的可行解, 是对偶问题的可行解。则存在。
- 无界性:若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解。
- 可行解是最优解时的性质:设是原问题的可行解, 是对偶问题的可行解, 当时,是最优解。
- 对偶定理:若原问题有最优解,那么对偶问题也有最优解;且目标函数值相同。
- 互补松弛性:若分别是原问题和对偶问题的最优解,则 。
非线性规划:
如果线性规划的优解存在,其优解只能在其可行域的边界上达到(特别是可行域的顶点上达到);而非线性规划的优解(如果优解存在)则可能在其可行域的任意一点达到。
某企业有
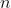
个项目可供选择投资,并且至少要对其中一个项目投资。已知该企业拥有总资金A元,投资于第
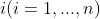
个项目需花资金
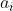
元, 并预计可收益
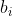
元。试选择佳投资方案。
设投资决策变量为
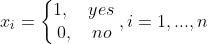
则投资总额为
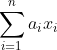
,投资总收益为
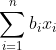
,限制条件为
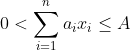
,和
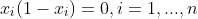
。
总的来说就是让投资总额最小,投资总收益最大,即
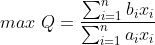
,
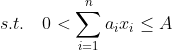
,