预备知识:
矢量场、矩阵正定负定、矩阵奇异。
1.李雅普诺夫稳定的定义:
系统,在平衡状态下,受到扰动,能够,经过足够长时间,恢复到平衡的,一种能力;
2.自治系统:
无外部输入作用的,平衡态为静止态的系统;
3.一般系统平衡状态和平衡点:
假设存在系统

,对于所有时间t,如果某个状态x满足
,则此状态x为系统的平衡状态,记作

;在式子
所确定的所有状态点,被称为平衡点;
3.线性系统平衡状态和平衡点:
假设存在线性系统
,其满足:在状态

处,

,则称

为系统的平衡状态;在式子
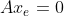
所确定的所有状态点,被称为平衡点;当系统矩阵
是非奇异矩阵时(行列式值为0,则为奇异矩阵,反之则为非奇异矩阵),系统存在唯一平衡点

;
4.大范围渐近稳定的系统:
不论系统的初始状态,在经过足够足够足够长时间,系统总是能够回到平衡点附近,且不断向着平衡点靠近,的系统;
5.线性系统中的大范围渐进稳定:
根据系统叠加原理,如果系统是渐进稳定的,那么系统一定是大范围渐进稳定的;
同样,如果线性系统的初始状态不稳定,那么系统也一定发散;
6.李雅普诺夫第一法(间接法):
对于线性定常系统,根据系统特征方程求解出特征根即可作稳定性判别;
数学定义:
假设存在线性系统
,其系统矩阵
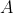
的特征值

具有负的实部,也就是说,系统矩阵
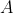
负定,函数图像是凹的,收敛于底部平衡点,那么该系统是李雅普诺夫稳定的;
对于非线性不严重的系统,利用线性化进行处理转化为线性系统进而利用特征根的方法判别;
7.李雅普诺夫第二法(直接法):
源自古典力学的观点:系统如果能量不能随时间而增加,那它最后必然趋于稳定;系统如果有一个渐进稳定的平衡状态,那么当系统运动到这个平衡状态附近时,其急需的能量会随时间的增长而衰减,直到到达平衡状态时获得最小值;
数学定义:
(1)假设存在系统

,假设存在具有连续一阶导数的标量函数
(到达平衡状态的一条路径),那么在其平衡点附近的一个邻域

假设存在:1)
正定且有界、2)
负定且有界,则可以认为系统在平衡状态的邻域
内是一致渐进稳定的;如果对系统任意初始状态都满足上述条件,那么该邻域覆盖了整个系统定义域,可以认为系统大范围一致渐进稳定;上述路径(标量函数)
,被称作李雅普诺夫函数;该函数不唯一,可以为简单标准的二次形式(能量形式):

,也可以是其它形式;(2)对于线性定常系统
,其在平衡状态

处,对任何给定的一个正定实对称矩阵Q,存在一个正定对称矩阵P,这二者满足
,也就是说:
,则称该系统是大范围渐进稳定的;
通过这个不等式,可以利用LMI(线性矩阵不等式)来进行求解:是否存在这个矩阵P。





















