贝塞尔(Bezier)曲线由一组多边折线（特征多边形）的各个顶点唯一定义，只需要很少的控制点就能够生成较复杂的平滑曲线。该方法能够保证输入的控制点与生成的曲线之间的关系非常简洁、明确，并且可以很方便的改变曲线的形状和阶次。
几种Bezier曲线介绍
贝塞尔曲线分为几种，一般2阶、3阶、4阶，或者更高阶的比较少见到。
- 一阶Bezier曲线：很显然是一条直线
2. 二阶Bezier曲线：
3. 三阶Bezier曲线：
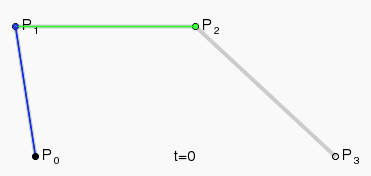
贝塞尔曲线具有众多特性，例如凸包性、对称性、几何不变性、仿射不变性、拟局部性，保证了生成曲线的平滑性、连续性和可控性。
三阶Bezier曲线的控制点确定
假设道路上已经有(n+1)个采样点Pi(i=0，1，...，n)，需要在相邻的每两个点P(i)和P(i+1)之间，用一条3次Bezier曲线连接。即由4个点确定， P0为起点、P3为终点，另外中间2个控制点P1和P2。
由四个控制点定义的平面三阶贝塞尔曲线可以形式化地表示为：
如图所示，在轨迹生成过程中，将目标车辆的中心点坐标作为起点P0，以目标车辆的驶意图为引导推理得到的目标点作为P3，其他两个控制点由车辆的约束条件计算得到。
由于车辆在运动过程中无法进行原地滑动移动，所以生成的曲线需要满足起点方向约束。另外,在执行换道和转弯动作时，在终点处行驶轨迹要遵从道路结构化特征的约束，行驶轨迹的切线方向和道路的走势要相同，所以生成轨迹的终点需要满足终点方向约束。为了满足上述方向约束，P1和P2分别通过以起点坐标为起点沿起点航向向前移动距离d，以终点P3为起点沿终点航向的反方向向后移动距离d得到。
简单来说，考虑到车辆起止点速度方向的连续性，即要求曲线函数的一阶导数连续。
clear
本文章为转载内容，我们尊重原作者对文章享有的著作权。如有内容错误或侵权问题，欢迎原作者联系我们进行内容更正或删除文章。
