CNN怎么看各个输入的贡献度

希望可以是你看到的最直白清晰的CNN讲解

点燃朋友圈的Alpha zero成为继Alpha go之后的有一个deep learnning产品，想必有很多人都想来了解深度学习，博主最近也一直在对深度学习进行探索，希望这篇文章可以和大家共同交流、探索。

这篇博客介绍的是深度神经网络中常用在图像处理的模型——卷积神经网络（CNN），CNN在图像分类中（如kaggle的猫狗大战）大显身手。这篇博客将带你了解图像在计算机中是如何存储的，什么是卷积，卷积神经网络的四个重要环节（局部感知、参数共享、多卷积核、池化），不会涉及复杂的公式。

计算机是怎么存储图片的

为了更好的理解计算机对图片的存储，我找了一个非常简单的图片，是一个385*385（像素）的jpg格式的图片，如图1所示，这个图片就是一个白色为底色，数字为黑色的数字“2”，也就是说，图片中只涉及两种颜色——黑与白（实际上并不是，因为图片在显示器中显示是一个像素一个像素的，黑白相间的地方其实并不是纯黑或者纯白的，将图片经过稍后描述的处理后也可以看出来，不过简单起见，我们就当它是黑白两色的）。

图1

可以使用scipy包中的imread函数将图片转换为数值型矩阵

from scipy.misc import imread
import pandas as pd
img = imread('2.jpg')
print(img.shape)
img_df=pd.DataFrame(img)
img_df.to_csv('2.csv')

上面的代码不用太过研究，能实现这个过程的方法很多。其实图片在计算机中就是数字，385*385=148225，图片中有148225个数字，每个数字其实就是该像素的颜色对应的数值（如白色是255），那么我们来看一下图片转换成为的矩阵是什么样子，如图2所示（我把csv按比例缩放了一下，看的比较清楚）。

图2

是不是惊艳到了！！！原来这个2在计算机中是这么存储的，好，我把局部放大一下，如图3所示，图3这个区域放大了，所以你可能看不太出来这是个啥，其实就是图4中红色圆圈的部分。

图3

图4

现在你可能明白了，其实每个图片都由若干像素点构成，每个像素点存储了该位置的颜色，其实还隐藏存储了另一个信息，就是位置。每一个像素点都有一对索引元组，例如（1，1）就是第一行第一列的像素点，如果写作（1，1，255），就是说第一行第一列的像素点是黑色，以此类推，也就是这样一个矩阵就完整的记录着图片的所有信息。

好，到了这里，聪明的你应该已经知道图片在计算机中的存储方式了。那么正式开始讲解CNN。

卷及神经网络

卷积

在开篇的部分，先简单给大家介绍一下什么叫做卷积，学过概率论的同学一定不陌生，那么白话解释一下啥叫卷积，很形象，就是“卷”，你假象一下，你把擦脸毛巾卷起来，成为一个圆柱体的卷，就是这个意思，抽象的说，就是将原来的对象变小一些，但又能保证原来图像中的信息尽量多的保留下来，可以看看下面这个卷积过程图。后面会有针对CNN卷积过程的详细解释，看看这个图，大概理解卷积是一个什么样子的过程就可以了，用映射两个字我认为是比较恰当的。

卷积过程图

图像到神经网络

这里的全部讲解基于大家了解了最简单的感知机，单层神经网络，多隐藏层神经网络的结构和参数估计方法（反向传播算法，具体可参见我博客中转载的文章《一文弄懂神经网络中的反向传播法——BackPropagation》）

为了更简单的理解CNN，我们先关注多隐藏层的输入层和第一个隐藏层（其实后面层数有多少都无所谓，一模一样的模式，大家假装CNN就是个单隐藏层的神经网络就好，不然多隐藏层画起来也麻烦，讲起来也麻烦）。网络结构如图6所示。

图5

这里，选取了两张比较直观和经典的图来展示个大家，如图6所示。

图6

现实中的图片可没有我例子这么简单，将它存成矩阵恐怕各位也看不出来他是个什么鬼，除非你能把每个位置的数字在脑海中脑部成颜色，然后将数万甚至数百万的像素粒按照矩阵在脑海中拼凑在一起。

好，我们关注图6的左图。假设我们输入的图片是1000*1000维的图像，在图像处理中，通常不使用这样的二维形式存储，而是将后一行拼接到前一行的最后，构成一个向量，对于这个1000*1000的图像，就构成了一个1×1000000，即长度一百万的一个数组，换句话说，神经网络的输入层（图5最左侧）有1000000个元素，假设（第一个）隐藏层，即图5中间的层的神经元个数与输入层相同，也是1000000，且输入层与第一隐藏层是全连接的，如图6中左图所示，那么我们就需要训练一个1000000∗1000000=1012 1000000 ∗ 1000000 = 10 12

第一法宝：局部感知

现在我们优化一下，假设图5的隐藏层中的每个神经元只与输入层的10*10个输入（即10*10个像素点）相连，（也就意味着每个隐藏层神经元不是和图片的全部像素都连接，而只是和图片的某一个区域的全部像素连接），那么两层之间连接线的个数，即参数的个数就变成了1000000∗(10∗10)=108 1000000 ∗ ( 10 ∗ 10 ) = 10 8 个，比起原来的1012 10 12 个参数，已经缩小了10000倍，但参数还是太多了，需要进一步的优化。

第二法宝：参数共享（以及卷积过程讲解）

既然参数太多了，每个神经元对应了100个参数，每个神经元对应的100个参数我们姑且叫它Pi P i 参数组，我们就会有P1，P2,……，P100000 P 1 ， P 2 , … … ， P 100000 这些参数组，假设P1=P2=……=P100000 P 1 = P 2 = … … = P 100000 ，也就是说每个神经元对应的参数组是相同的，那么我们其实就只有一个含有100个未知参数的参数组，瞬间，参数数量就成为了100，是一个可以轻易进行训练的数量级。

你可能要问，这样的假设合理么，答案是：从理论和思想上来说，是合理的，从实践结果的证明来看，是非常好的。这个假设意味着什么呢？这100个参数（就是卷积操作）是一种特征提取，该方式与位置无关。这其中隐含的原理则是：图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上，所以对于这个图像上的所有位置，我们都能使用同样的学习特征。再说白一点儿，一张图片，左半边和右半边的特点，风格一般情况下是一样的，哪怕毕加索这种抽象派大师，喜欢画左右脸不一样的抽象人物，其左右脸的风格也是相同的，找一个毕加索的画作，让你看，你可能一眼就看出来作者十有八九是毕加索，遮住图片的左侧，你可能也比较确认是毕加索的画作，遮住右边也是一样的，这个说法不太严谨，这个“风格”其实就是图像中的各种统计特征（图像编程了数值，那么任何位置都会有一些统计指标，比如极值，均值等）。

这个10*10的参数矩阵，就是所谓的卷积核！！！

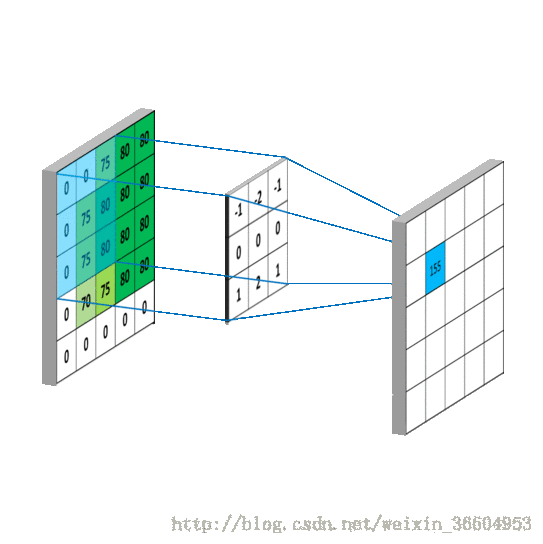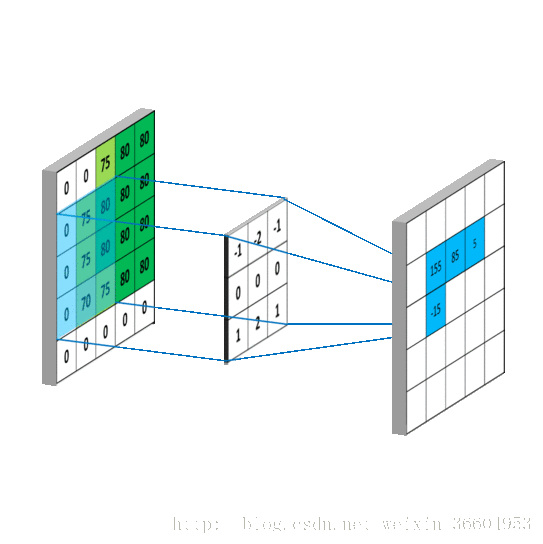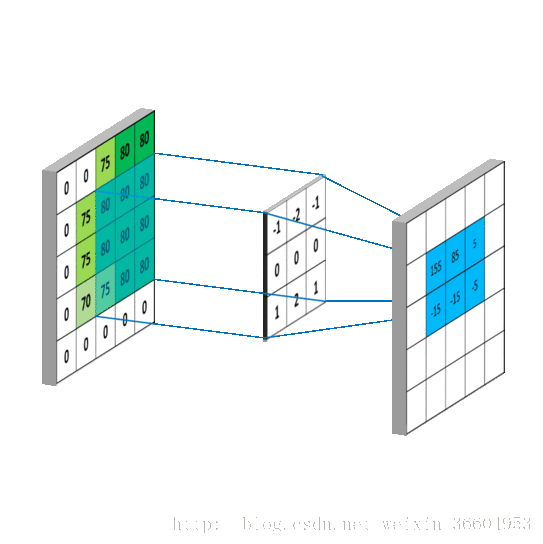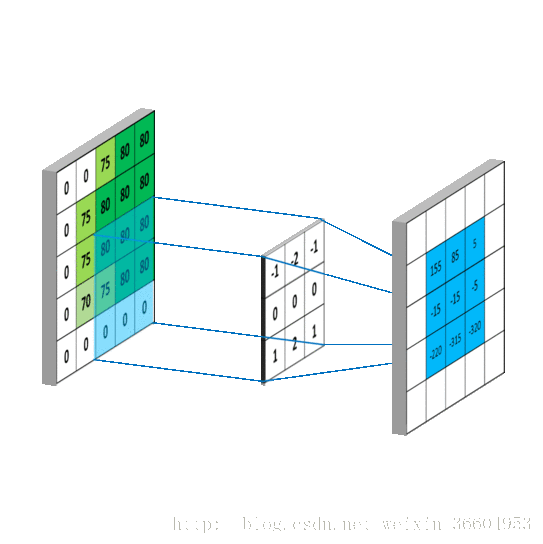
卷积的过程可以参考图7所示（动图来源于 ，不要怪我懒，我是真的不太擅长搞一些特别清楚明白的动图，所以只能看到好的就拿过来借鉴一下）。

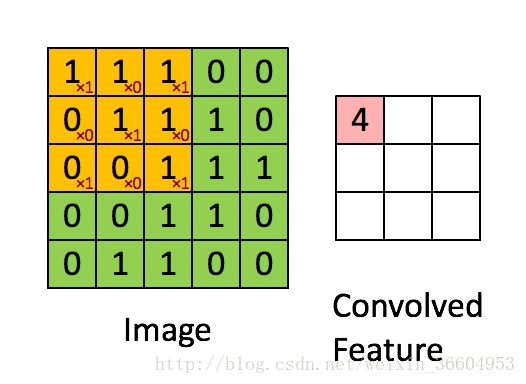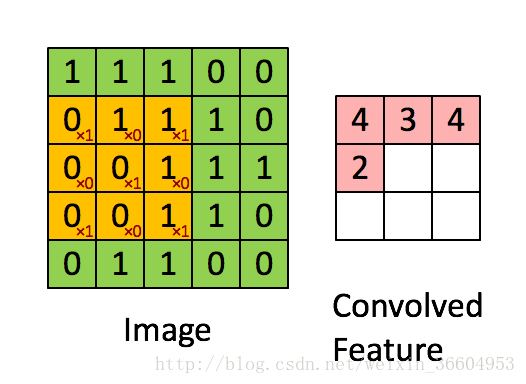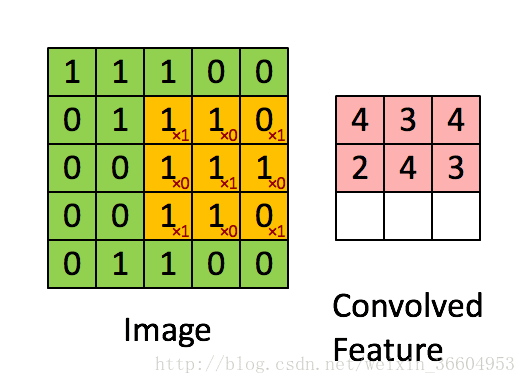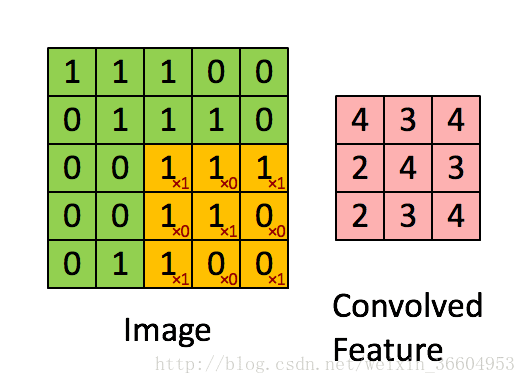
图7

我来详细解释一下，图7的左图是一个5*5的图片，转换为了其对应的像素矩阵。图7右侧是一个使用3*3的卷积核进行卷积后得到的结果，卷积核心作用在图像上的过程是这样的：用一个3*3的窗口去挨个遍历左图的5*5的矩阵，可以得到9个3*3的矩阵（这个理解吧，小学生应该也能算出来），用这9个矩阵分别与图7右侧的卷积核做对应相乘再求和，就是卷积。打个比方，左图第一个3*3矩阵应当为

100110111(1) (1) 1 1 1 0 1 1 0 0 1

假设我们的卷积核就是图7左图中给出的卷积核（图7每个小方块右下角的元素构成的军镇就是卷积核），即：

101010101(2) (2) 1 0 1 0 1 0 1 0 1

矩阵（1）与卷积核进行对应元素相乘再求和，即：

1∗1+1∗0+1∗1+0∗0+1∗1+1∗0+0∗1+0∗1+1∗1=4 1 ∗ 1 + 1 ∗ 0 + 1 ∗ 1 + 0 ∗ 0 + 1 ∗ 1 + 1 ∗ 0 + 0 ∗ 1 + 0 ∗ 1 + 1 ∗ 1 = 4 ，因此图7右侧左上角的元素即为4，依次类推，得到了一个3*3的映射结果。也就是说，假设我的图像是M*M维的，而卷积核是N维的，那么卷积操作后会得到一个（M-N+1）*(M-N+1）的矩阵。

有人又要问了，这个卷积核怎么定呢？
CNN的目的就是通过反向传播算法，训练出最好的卷积核，这个卷积核就是我们的参数。
初始的卷积核可以使用平均矩阵，对于一个3*3的卷积核而言，大可使用（3）中的矩阵：

191919191919191919(2) (2) 1 9 1 9 1 9 1 9 1 9 1 9 1 9 1 9 1 9

好了，参数已经优化到了很成功的量级，接下来，还有什么可以优化的么？

第三法宝：多核卷积

上面所述只有一个10*10的卷积核，有100个参数，显然，特征提取是不充分的，我们可以添加多个卷积核，比如32个卷积核，可以学习32种特征。在有多个卷积核时，如图8右侧所示：

图8

每一个局部感知野不止像图8左侧那样，只由一个卷积核进行卷积操作，而是对应多个。这个过对应到网络可能比较难想想，我也想了很久怎么能把这个过程展示清楚，所以想引用LeCun的LeNet-5网络结构，即图9所示的网络结构来给大家看看。看图9左起第二个层，里面有很多个正方形（即矩阵，每个矩阵都是通过不同卷积核进行卷积后得到的结果），也就是说这个隐藏层是有“厚度”的，一个卷积核就可以得到一个正方形，6个卷积和就得到6个正方形，构成了一个有厚度的层，这里的结构大家把它想成3D立体的，有厚度这个概念，就可能好理解一些了。

这样，通过多个卷积核的操作，对图像的特征提取就更加充分了。

图9

第四法宝：池化-Down-pooling（下采样）

有时图像太大，即使我们参数不太多，但图像的像素实在太多，导致卷积操作后，我们得到的结果（图9中左起第二个层中的每一个正方形中的元素数量太多）仍然过大。我们需要减少训练参数的数量，它被要求在随后的卷积层之间周期性地引进池化层。池化的一个目的是减少图像的空间大小。池化在每一个纵深维度上独自完成，因此图像的纵深保持不变。池化层的最常见形式是最大池化。

还有一个目的是保持平移不变性。 卷积对输入有平移不变性，池化对特征有平移不变性。平移不变性是什么呢？因为卷积核是在输入图或者feature maps上滑动，或者说平移，每次平移时，因此假设使用max pooling，会过滤掉那些不明显、未被激活的特征。

深度学习，自然有多个隐藏层，对应到CNN中，就是有多个卷积层，且有多个卷积核，那么原始图像的过大会导致卷积后的结果过大。其实我们可以对卷积后的结果进行一个缩小的过程，使下一次卷积更加轻松。这个缩小过程就是池化。

为了解决这个问题，首先回忆一下，我们之所以决定使用卷积后的特征是因为图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征)，同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling)，有时也称为平均池化或者最大池化 (取决于计算池化的方法)。

池化的过程如图10所示。

图10

在这里，我们把步幅定为 2，池化尺寸也为 2。也就是对图10左侧4*4的矩阵，用一个2*2的窗口去以2为步长去遍历，再直观的说，我们按照横向和纵向两条中轴线将他切成4个2*2的矩阵，然后取每个矩阵的最大值，作为池化后的结果，就得到了图10右侧的池化结果。最大化执行也应用在每个卷机输出的深度尺寸中。正如你所看到的，最大池化操作后，4*4 卷积的输出变成了 2*2。

除去最大池化，有平均池化，L2池化等等，这里不做过多讲解。

输出

其实深层的CNN和上述过程一样，首先有输入层A，初始化一个卷积核，然后进行卷积，得到了第一个卷积层B（如果有i个卷积核，就会在同一层中得到B1,B2,……,Bi B 1 , B 2 , … … , B i ），然后进行池化，得到一个池化层C（C1,C2,……,Ci C 1 , C 2 , … … , C i ），然后进行下一次卷积。。。一个卷积层，一个池化层，重复下去，假如是做分类任务，那么当层数到达了我们指定的层数，然后到达了输出层，CNN 中的输出层是全连接层，其中来自其他层的输入在这里被平化和发送，以便将输出转换为网络所需的参数。通过前向传播过程到达label，然后进行反向传播，进行参数的计算。

补充一个CNN各过程的简单例子

再多说一些

之前说的多个卷积核，必然得到多个输出，这些输出就是一个个的矩阵，而这个矩阵本身其实也是图片（就像原始图像一样），这些图片叫做feature maps，由于feature maps 是由不同卷积和得到的，卷积和是一种特征提取，与输入的图像进行卷积后，相当于再做“激活”动作，激活后得到的feature maps 就是具有对应卷积核特征的图片，卷积核其实就是滤波器，符合我特征的，激活，不符合的，死着呆着，换做另一个卷积核，可能之前被激活的这次就没有，而之前死的这次被激活了，所以feature maps 是被卷积核过滤出来的具有不同特征的图片，最后的输出层就是汇总了这些特征的图片，也就是说，到达输出层这里的图片，具有前面每个卷积核的特征，或者可以理解为，到达输出层的图片是输入图片的最明显的特征的集合体，就像人类对一个图片做判断，一个小狗在草地上，另一个图片是一个小猫在水里，那么你判断图中的动物是猫还是狗，几乎不会受到草坪或者水面的影响，而是基于图片主体本身，或者说基于猫和狗的不同特征，这就是CNN在模仿人类的判断方式。

最近比较懒，可能之后有时间会上一些CNN做图像分类的代码，对于图像，我也是新手，所以希望与大佬们多多交流探讨！！！