文章目录
- 一:微积分简单理解-以推导圆面积为例
- 二:导数的概念
- (1)导数的意义
- (2)导数概念
- (3)可导
- 三:微分的概念
- (1)微分概念
- (2)可微
- 四:导数与微分的几何意义
- 五:连续、可导和可微之间的关系
一:微积分简单理解-以推导圆面积为例
众所周知,圆的面积公式为

面对这样一个圆(假设),为了求出面积,我们可以将这个圆划分很多个圆环,然后把这些圆环的面积加起来
- 当然划分为其他形状也是可以的,只不过划分为圆环保留了很好的对称性

对于这个圆环,可以将其剪开然后拉直,得到一个梯形

但为了研究方便,这里认为他是一个类矩形
- 那么它的长度即圆环的周长就很容易得到,为
- 厚度是可变的,因为这取决于你把圆环划分的多粗或者是多细,这里定义为
(环与环之间微小的半径差)
于是,这个圆环或类矩形的面积就很容易得到了,便是

虽然这个近似存在一定误差,但是你会发现,如果随着越来越小(圆环划分得越来越密),这个类矩形上下长度就会越来越接近,误差也会越来越小
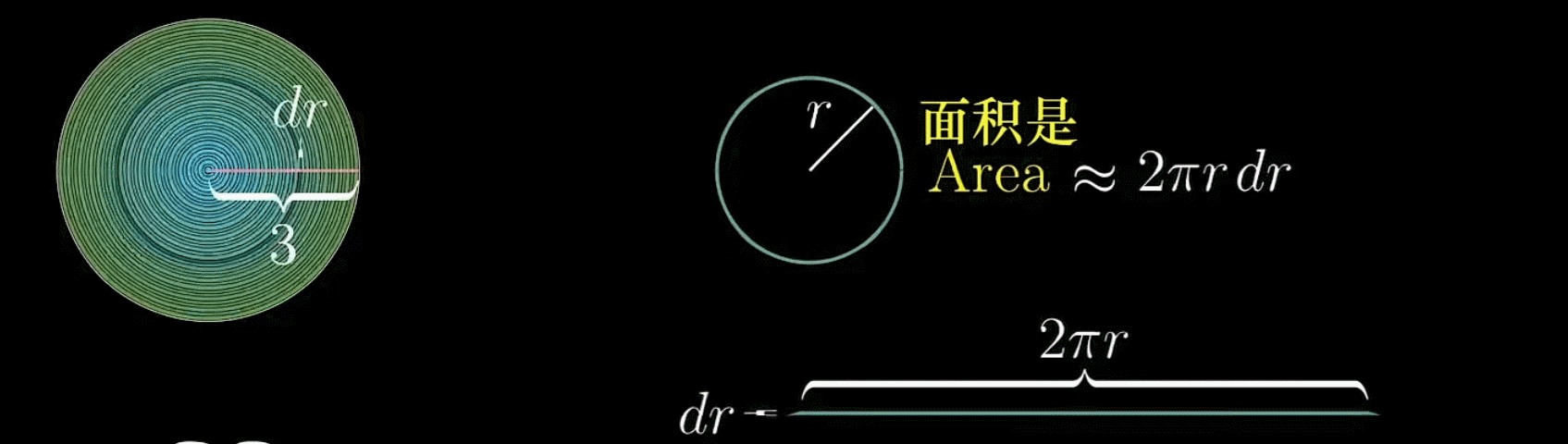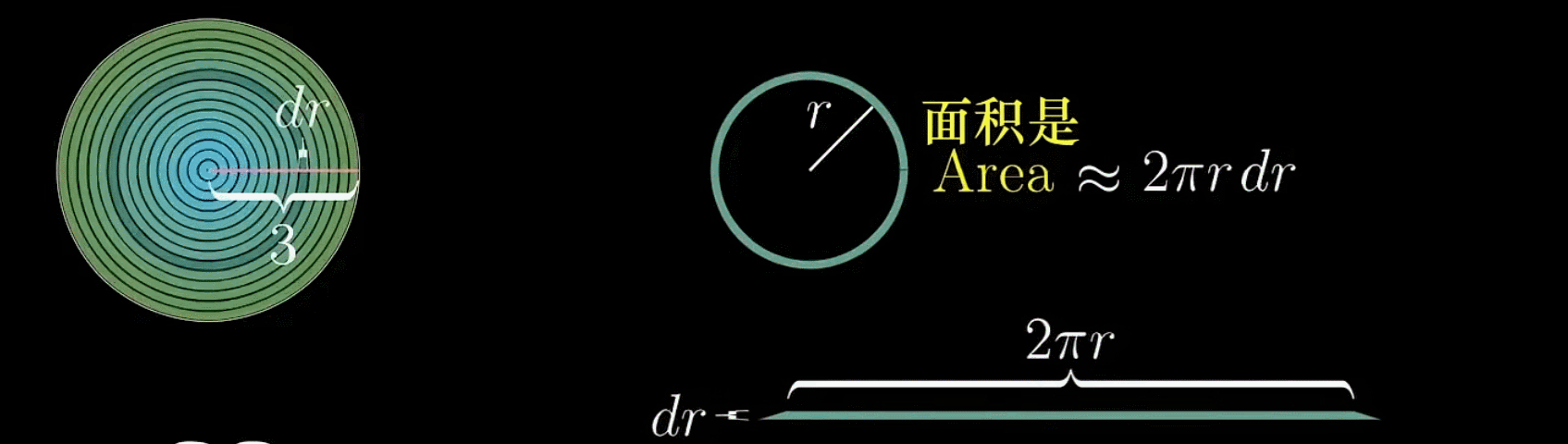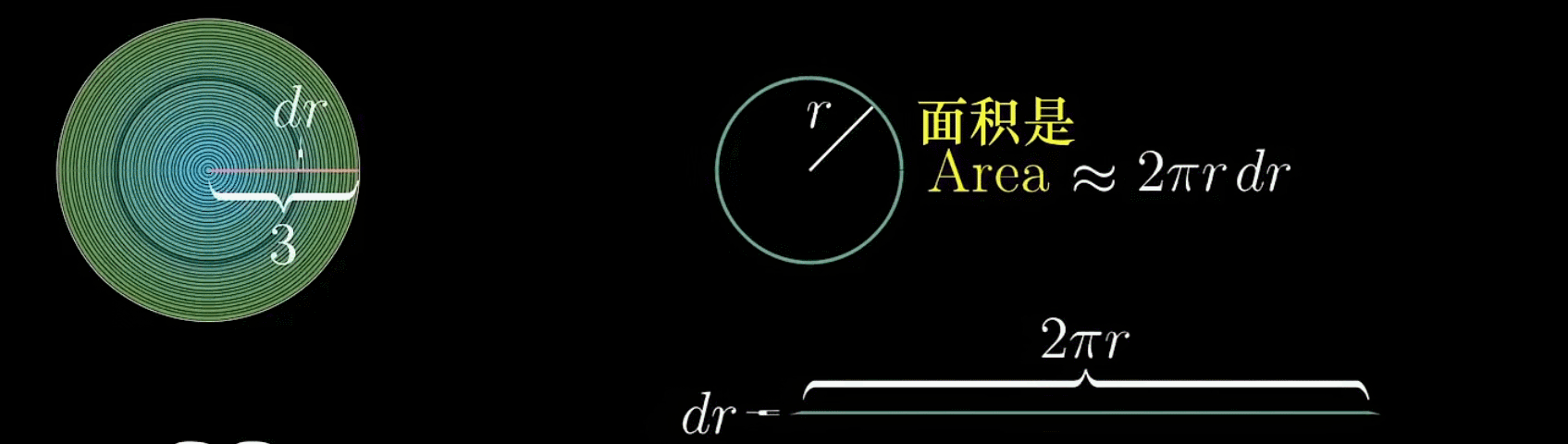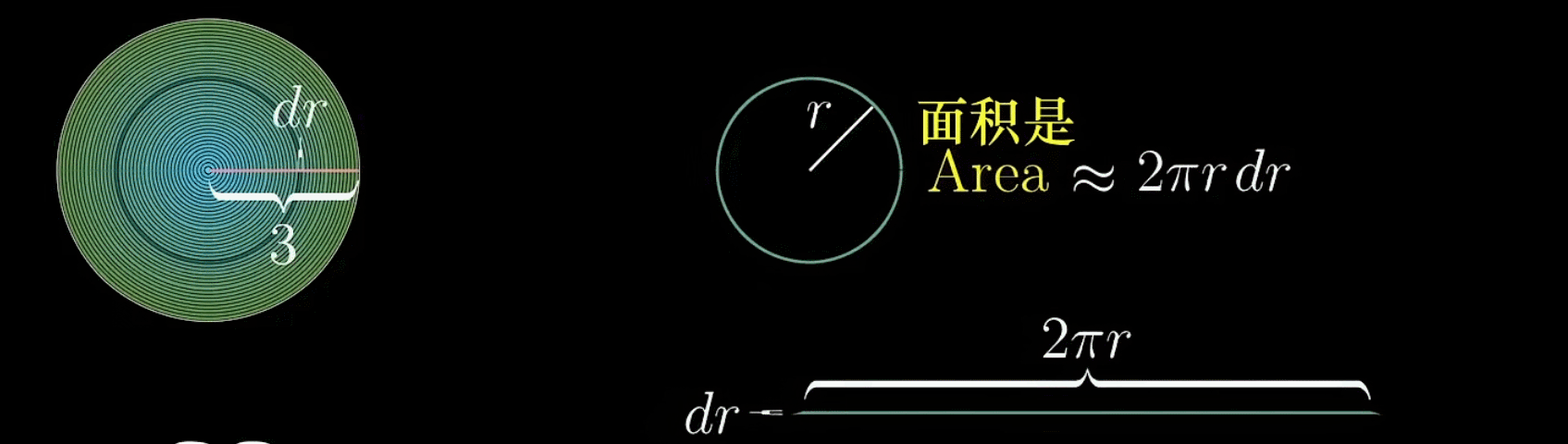
现在,我们把所有圆环全部取下来,剪开后竖直排列在坐标轴上
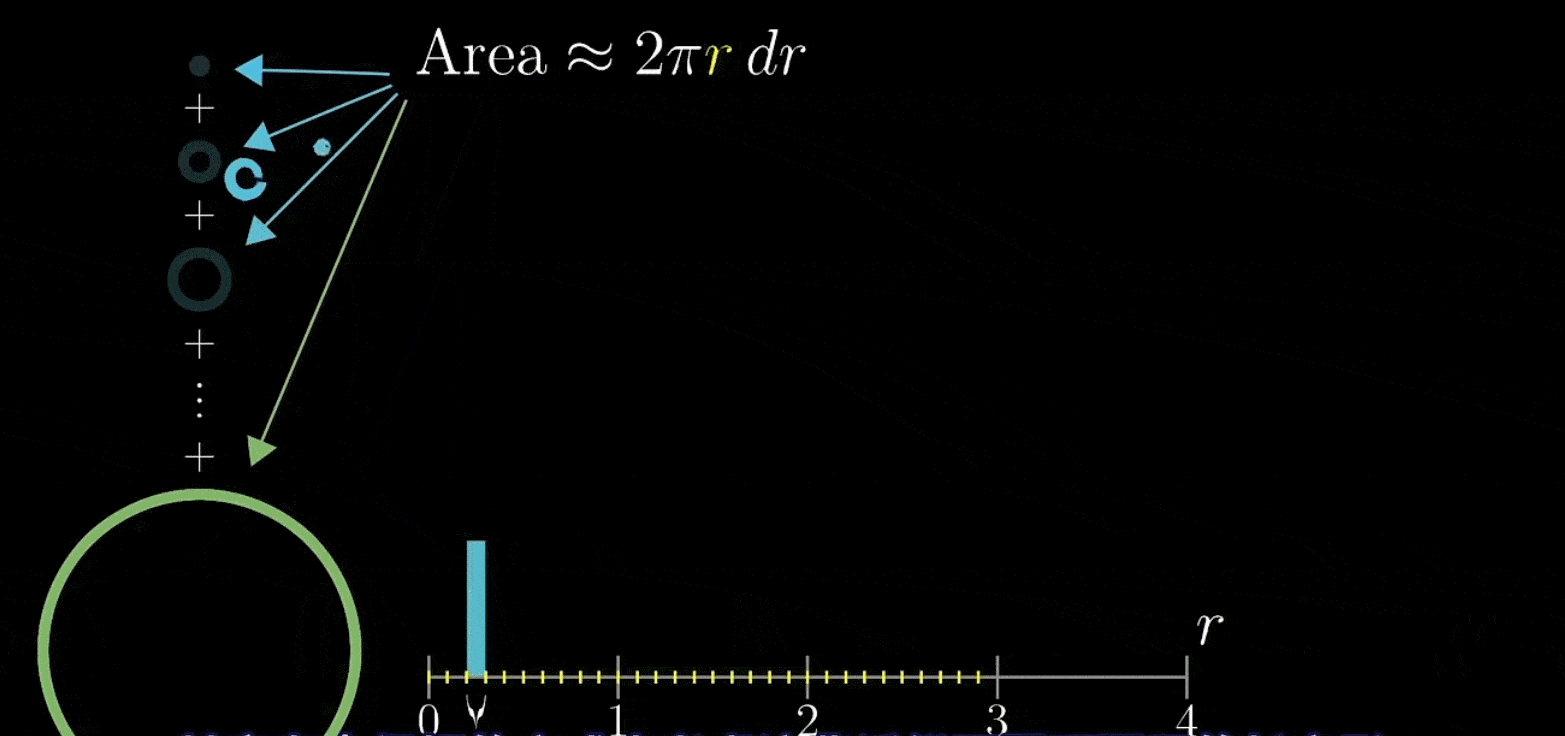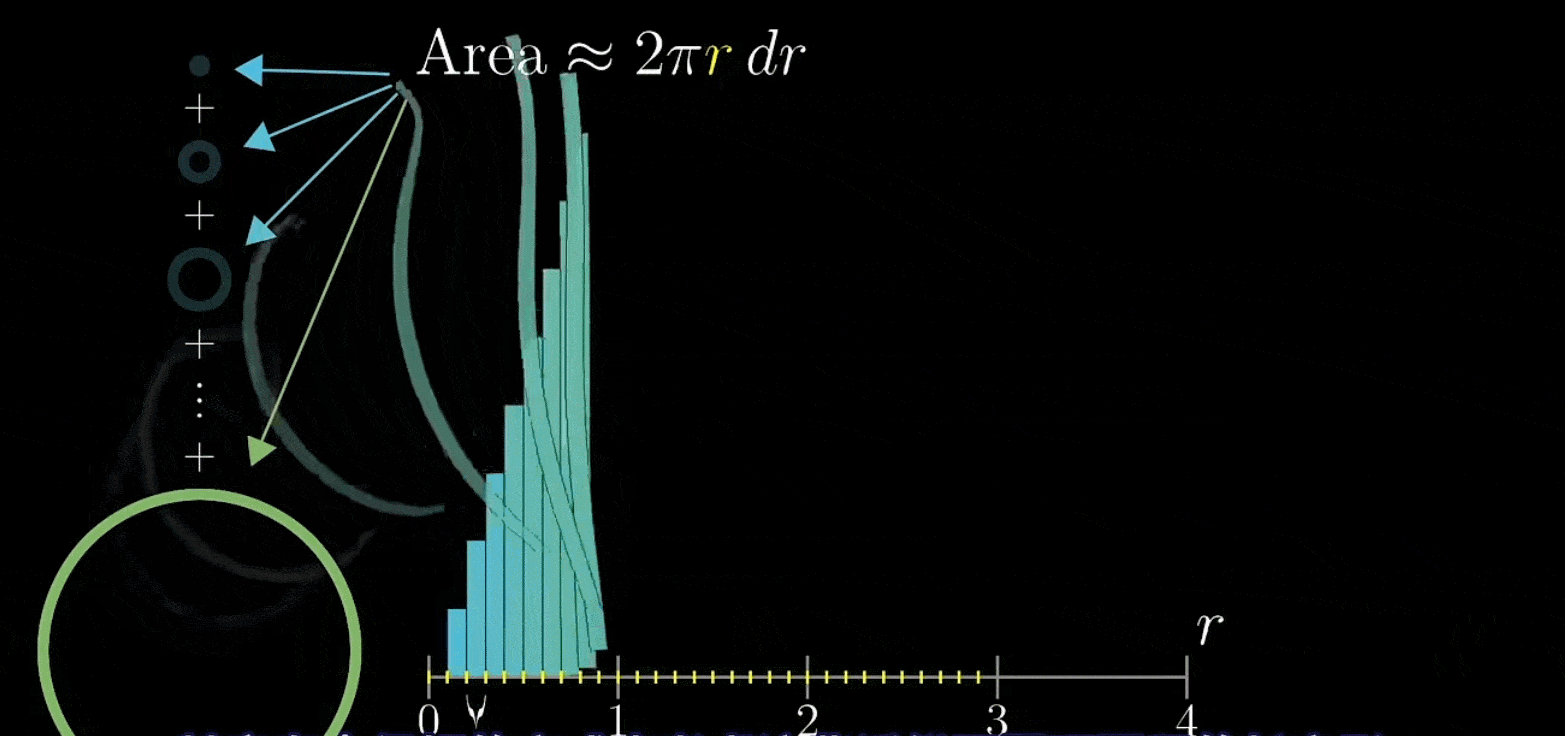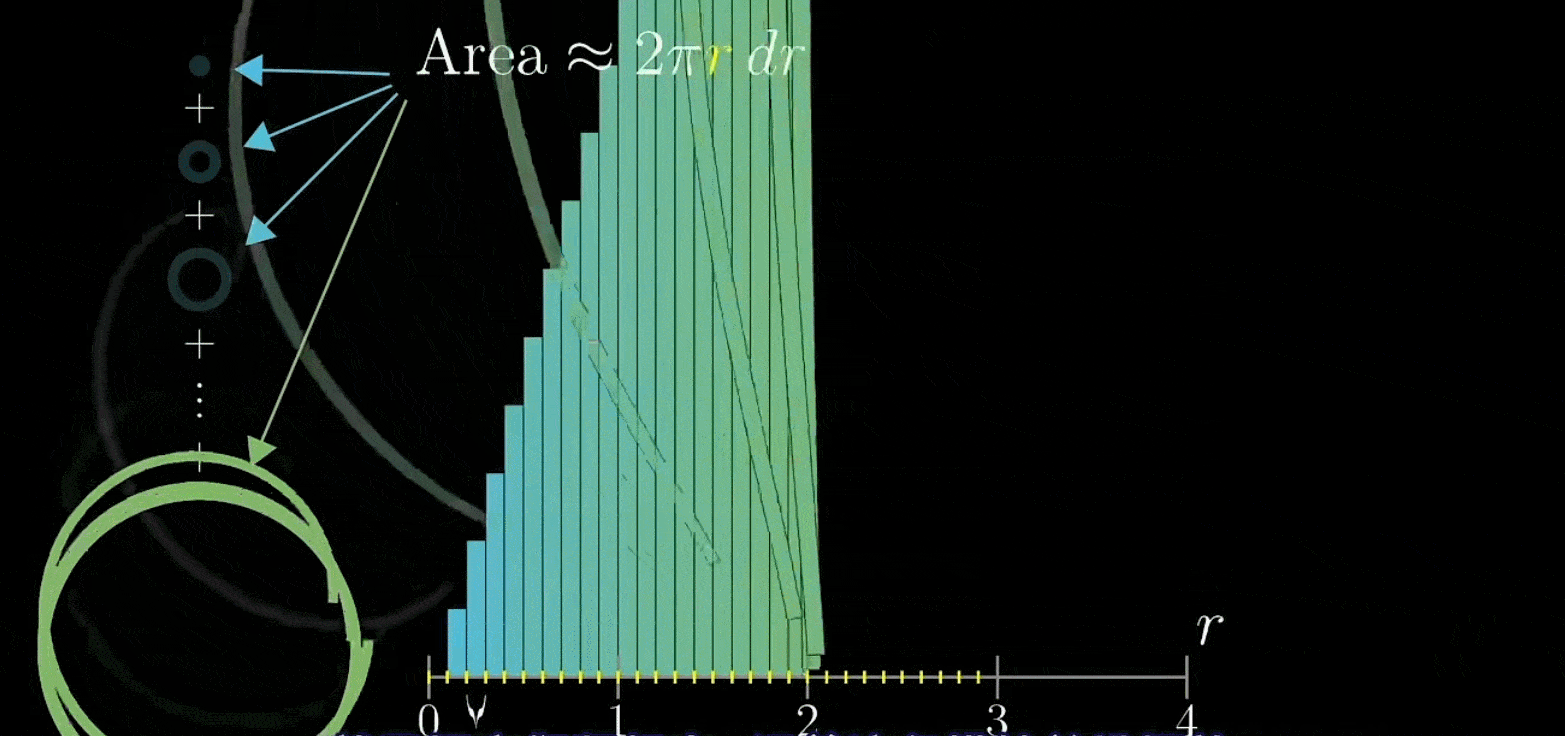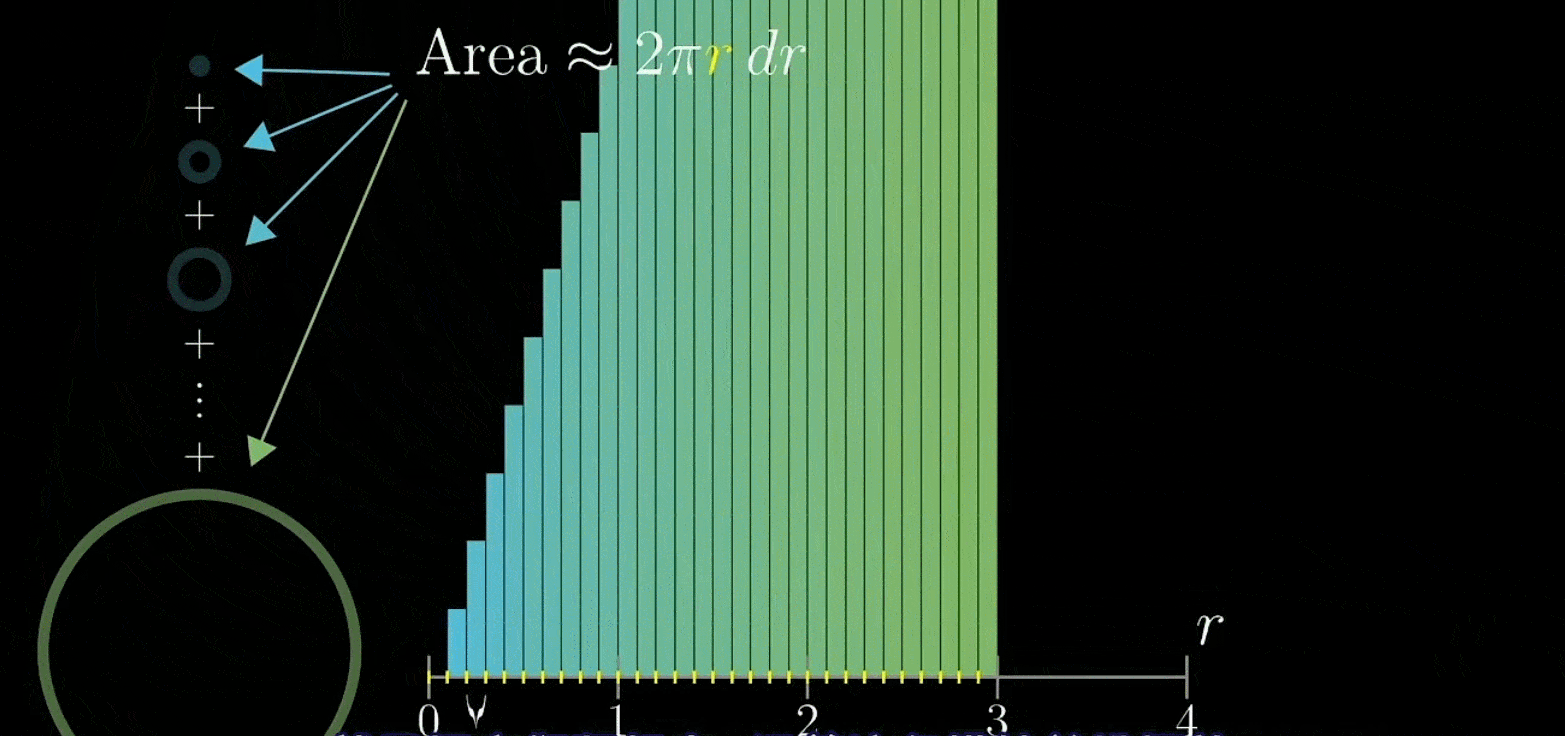
接着过这些类矩形左上断点画出一条直线(应该不难理解)

接着让无限小,你会发现这些面积合起来就是图像下方三角形的面积,也即

二:导数的概念
(1)导数的意义
下面的图描述了一辆汽车从起步到加速、减速然后停止的过程(历经10s)
“路程-时间”图我们再熟悉不过了,当然这条曲线也会对应一条

这两条曲线存在着对应关系,反映出的是导数的含义
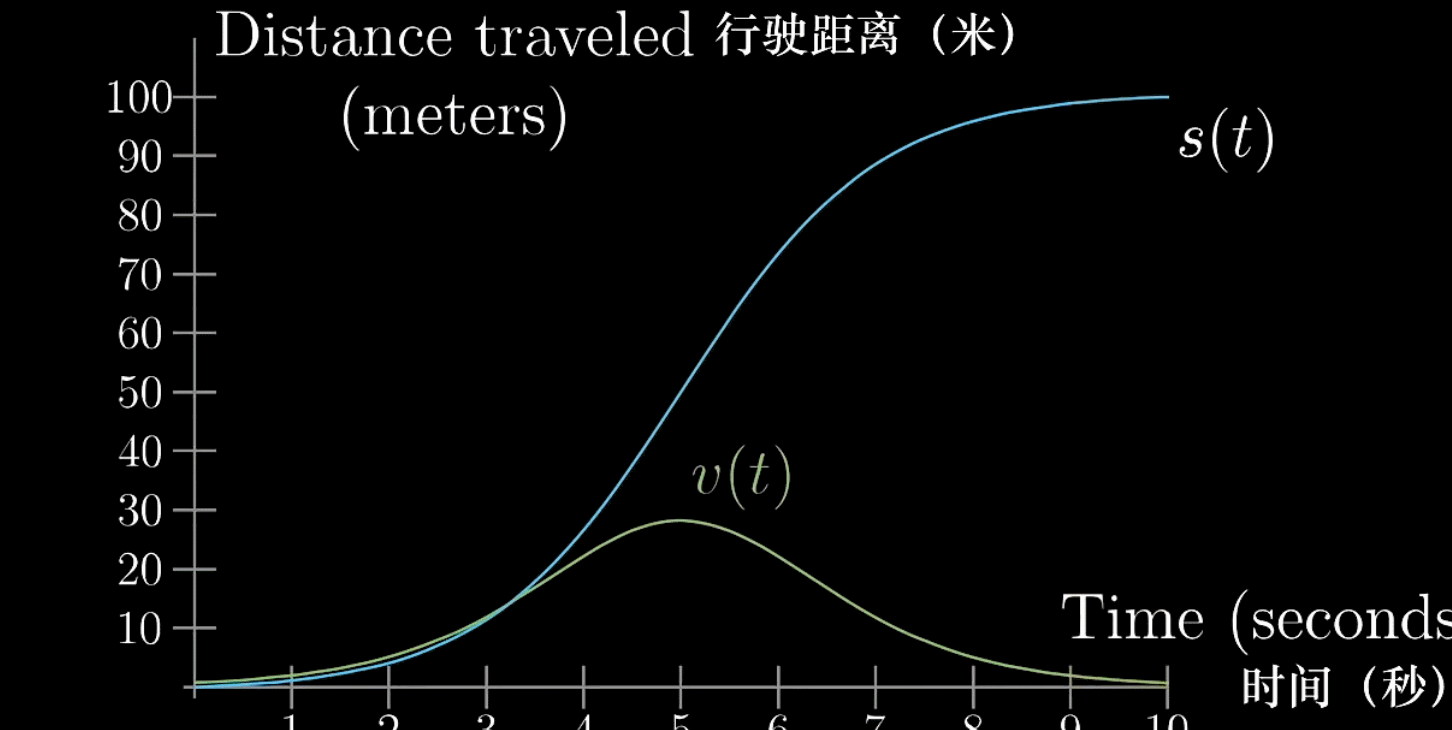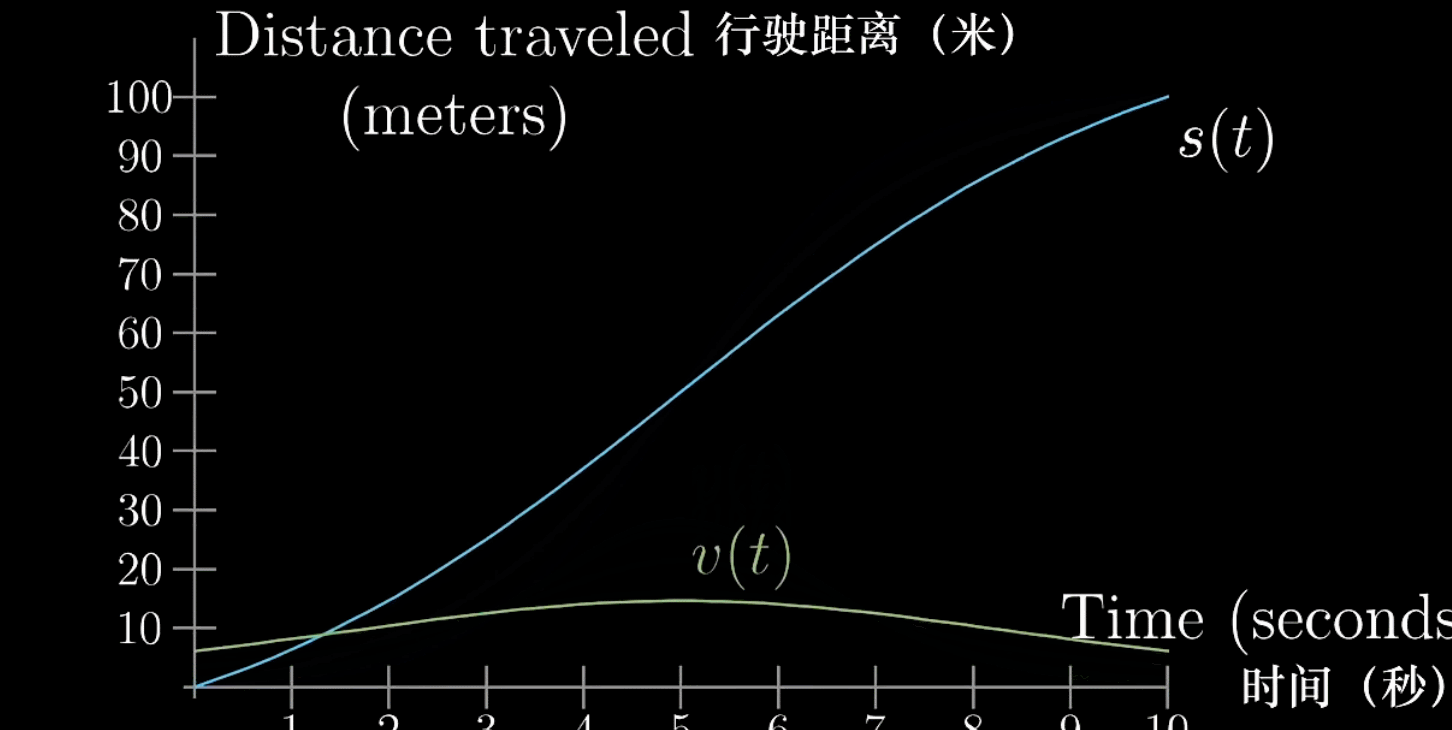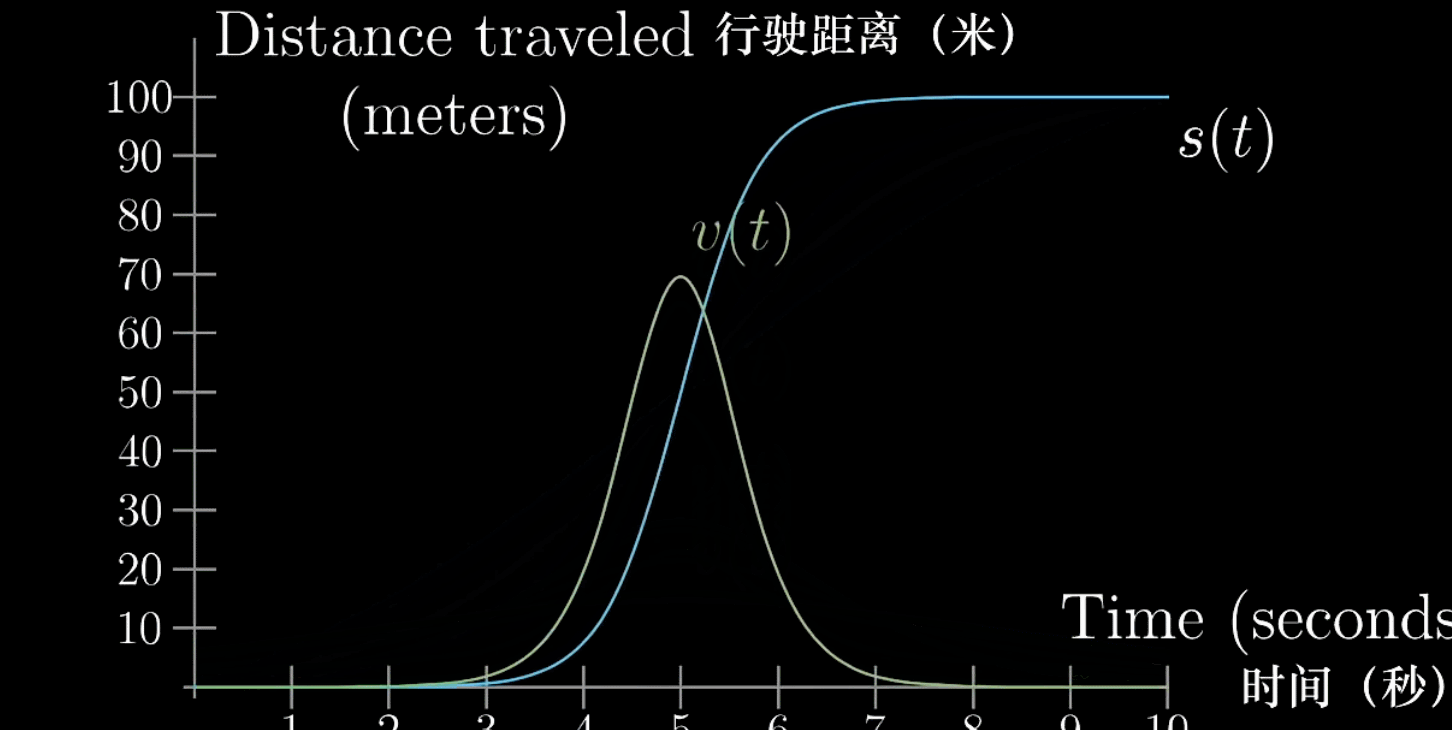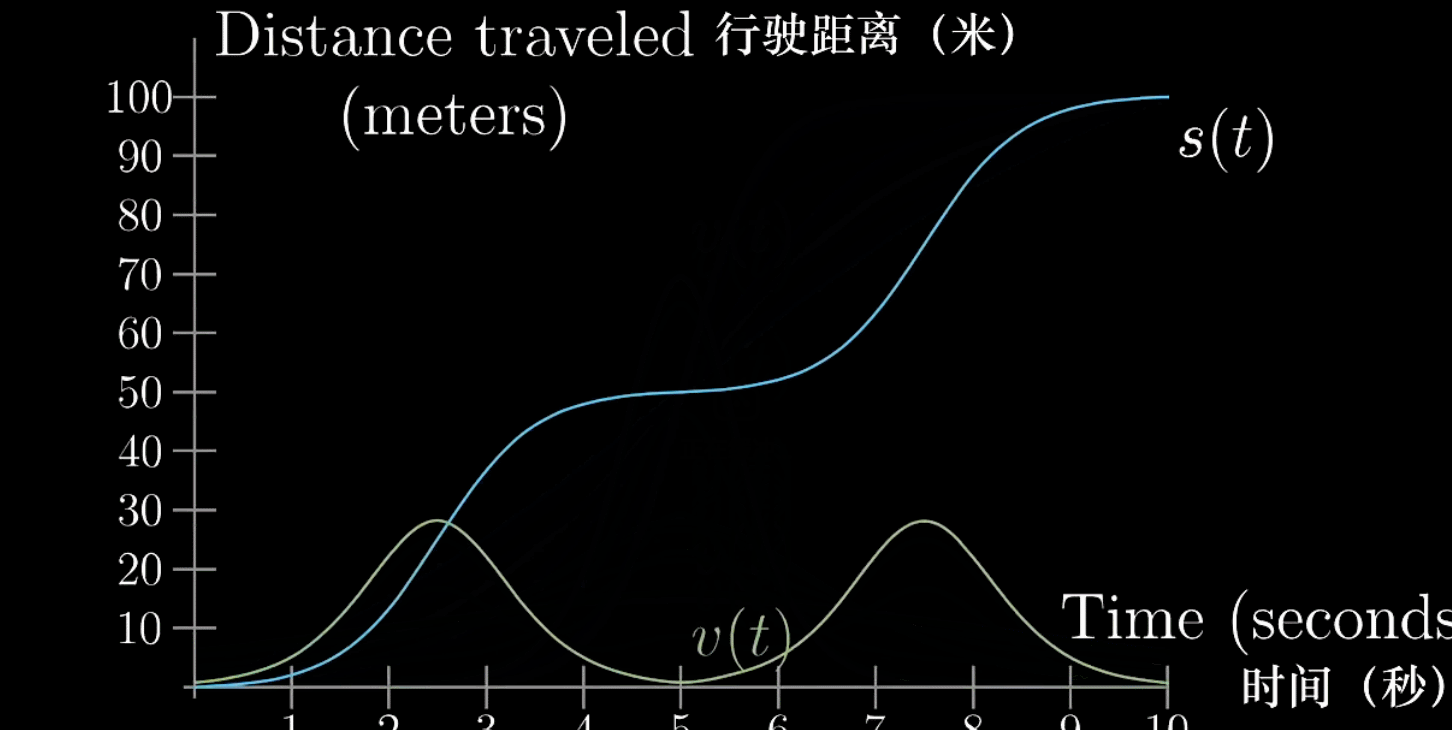
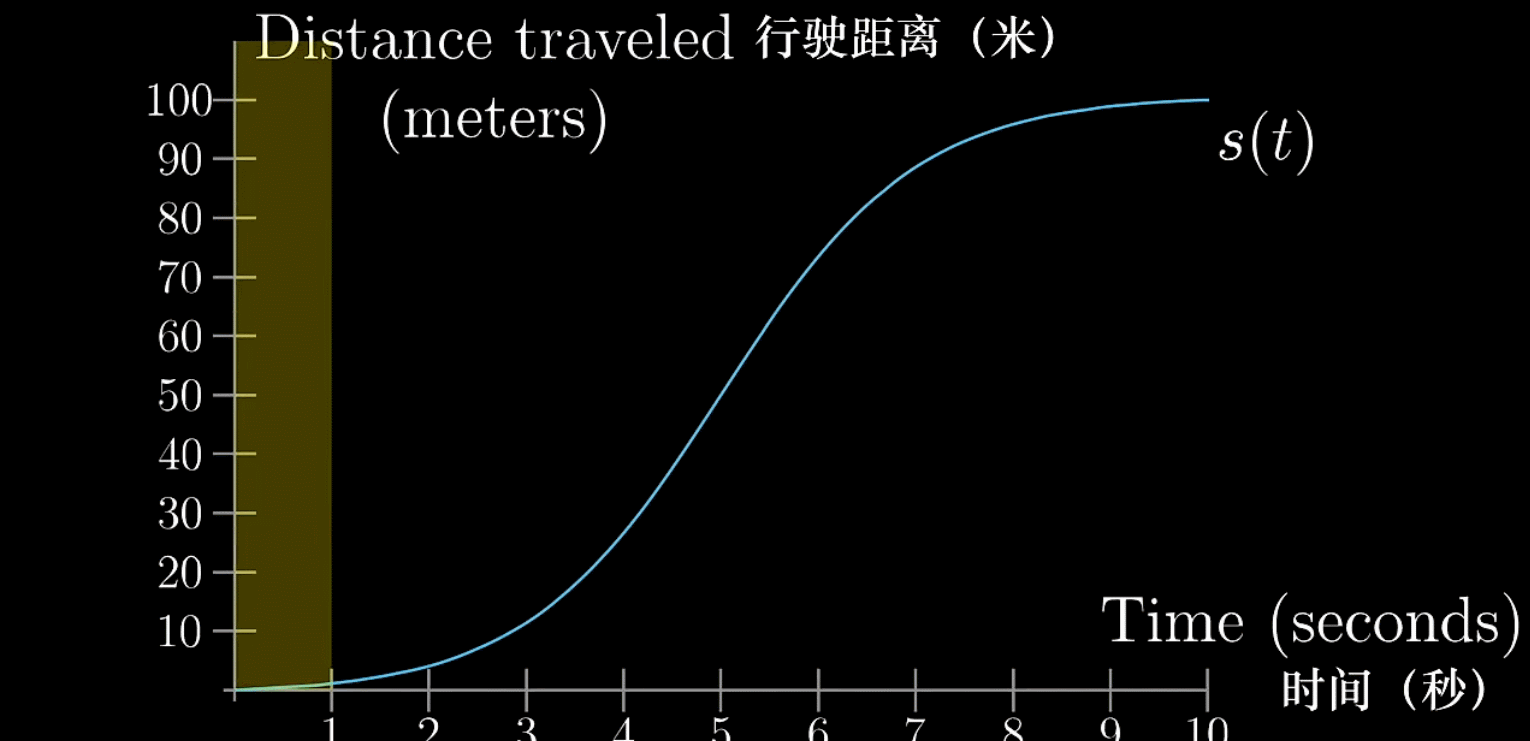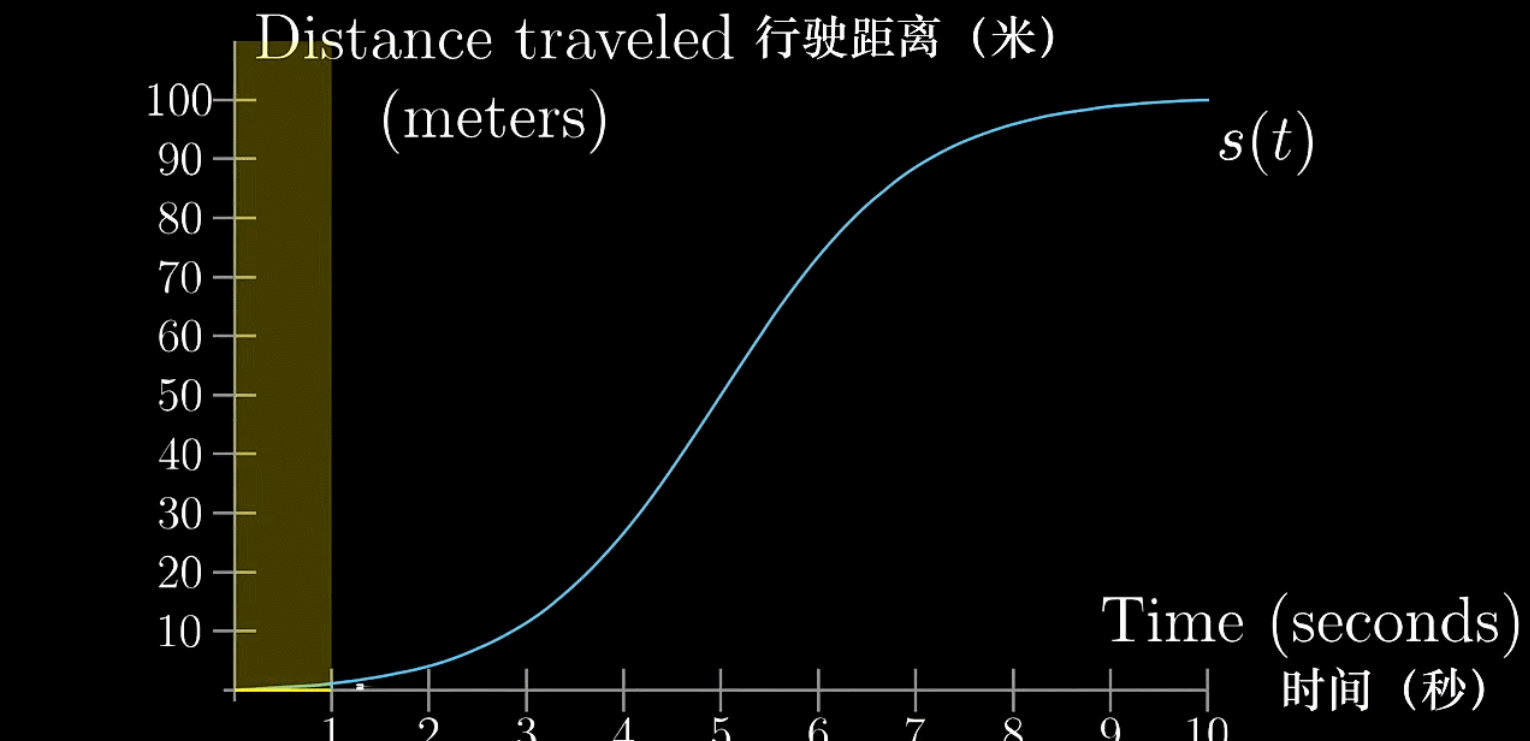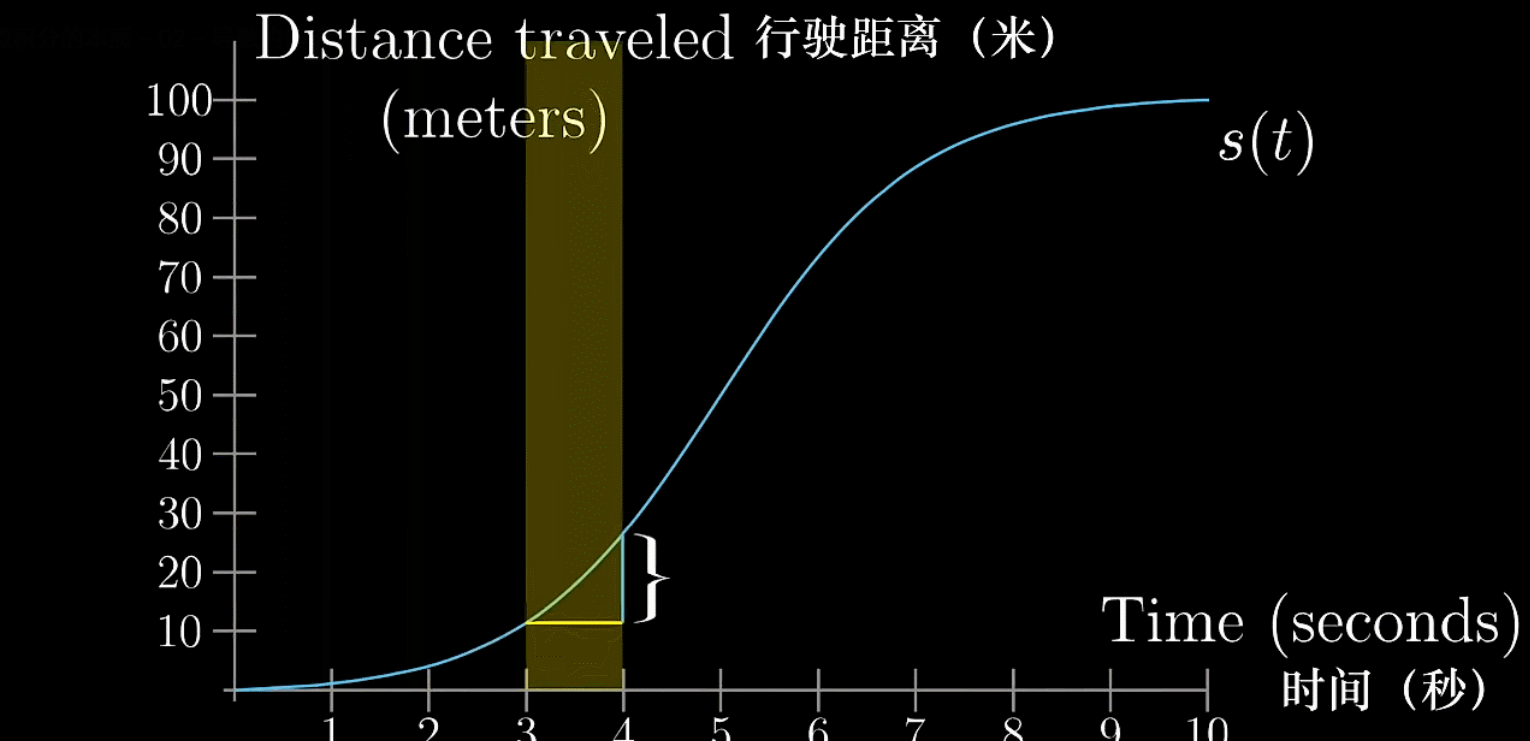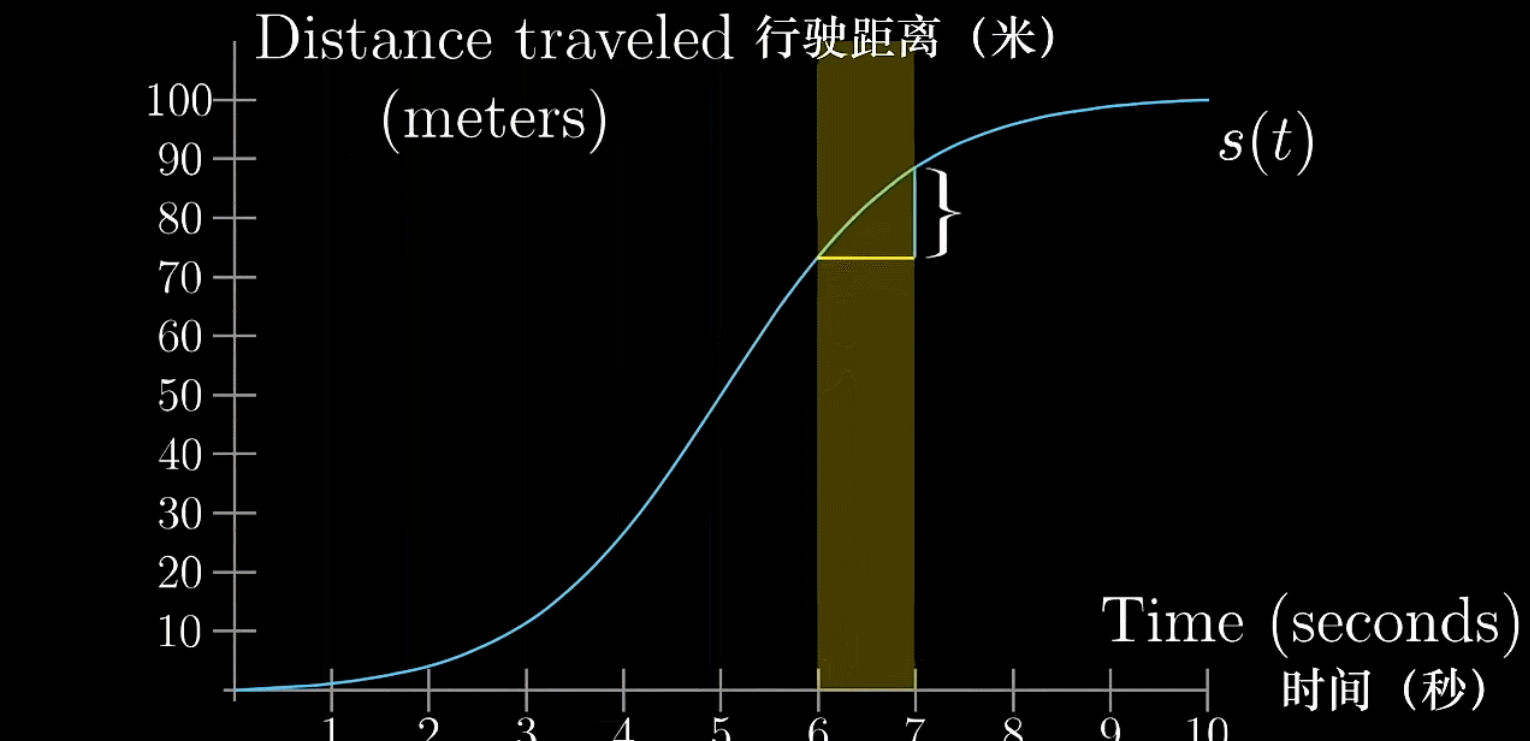
观察曲线,发现每一个
都对应了一个速度
,称其为瞬时速度。但是这却和速度的定义式相违背,因为计算速度需要比较两个时间点上的距离

其实,瞬时速度、瞬时变化率这些说法本就是矛盾的,因为只要涉及到变化怎么可能是单独某个点。因此在实际生活中,例如车速表中的速度实际上是用极小的时间段的距离的变化量来代替所谓的瞬时速度的
- 距离变化量:
- 时间变化量:
- 任意一点速度:

返回到原图,可以看做是关于
的函数
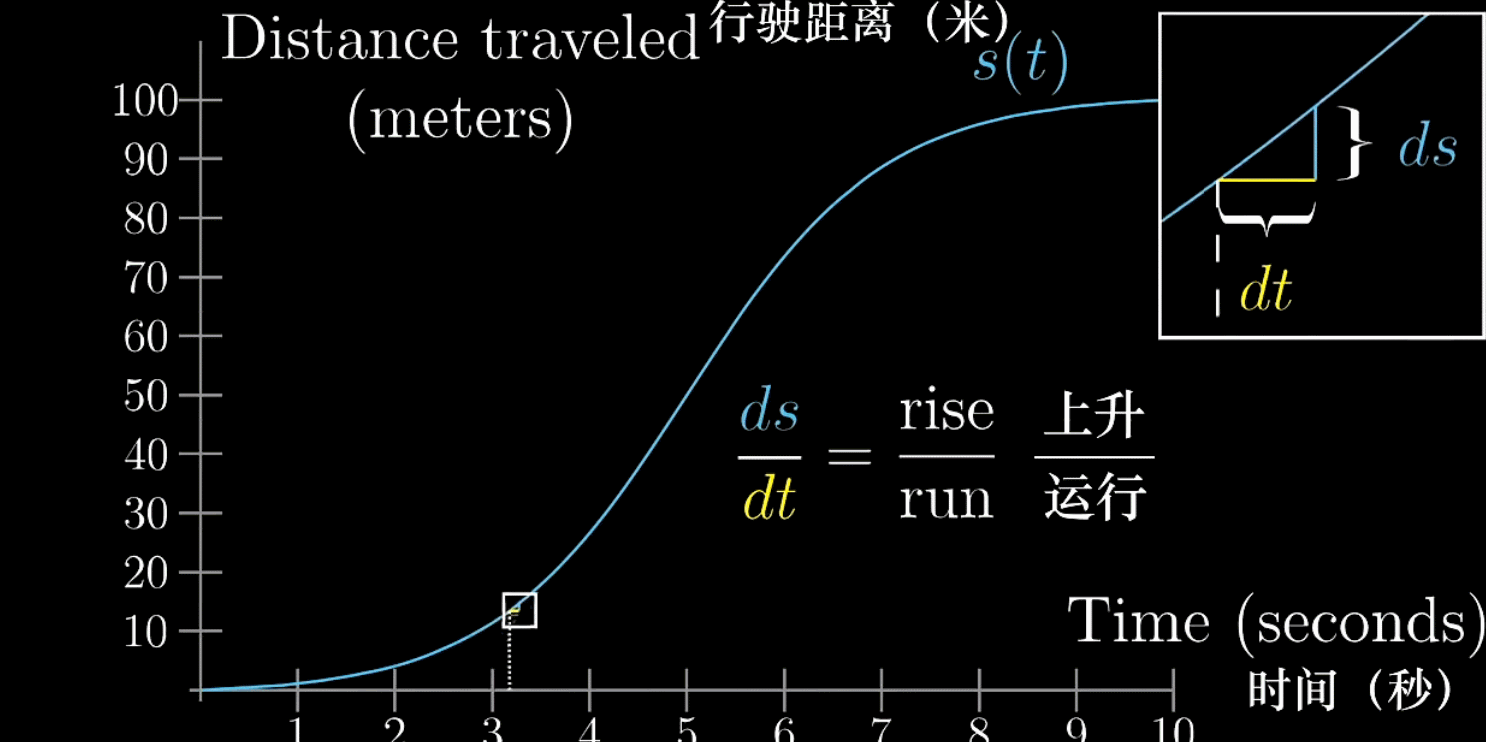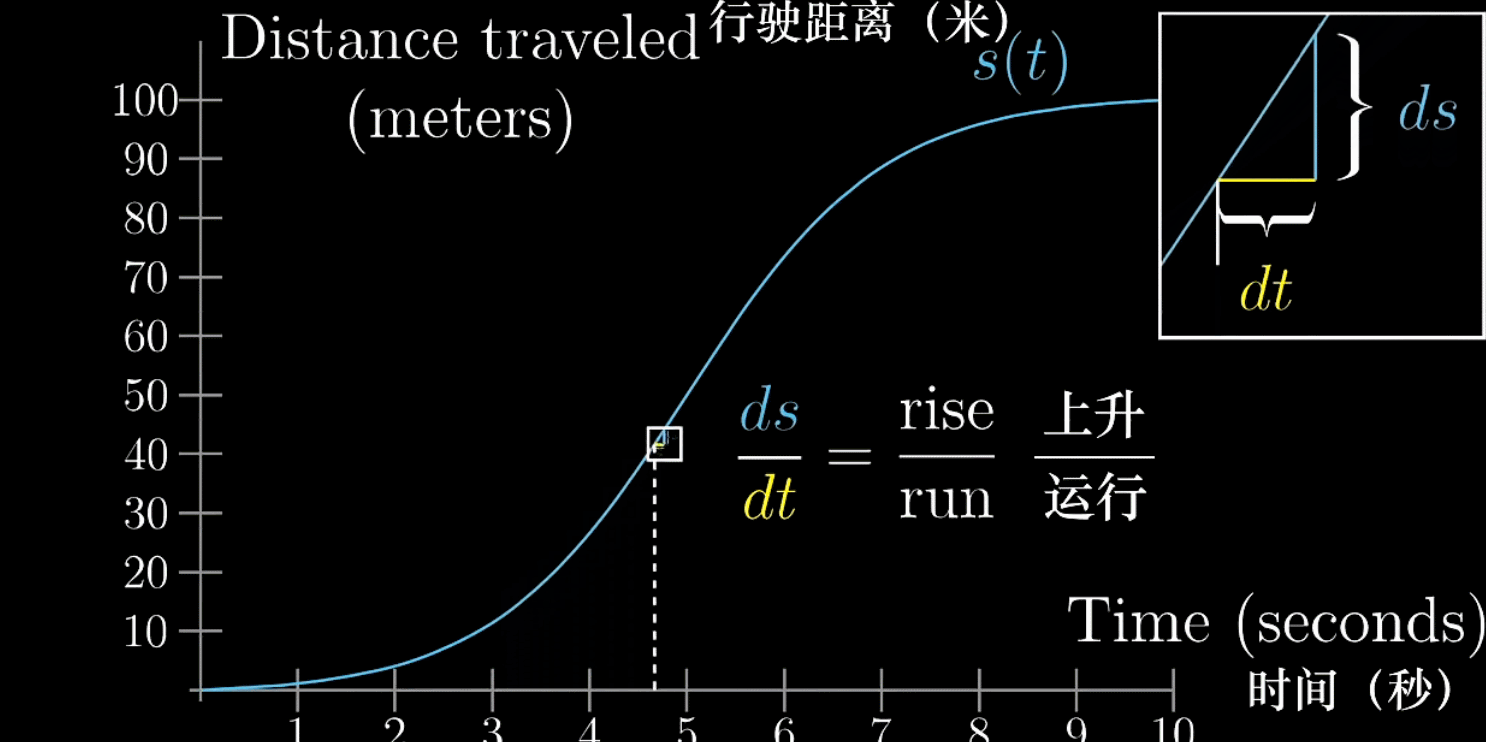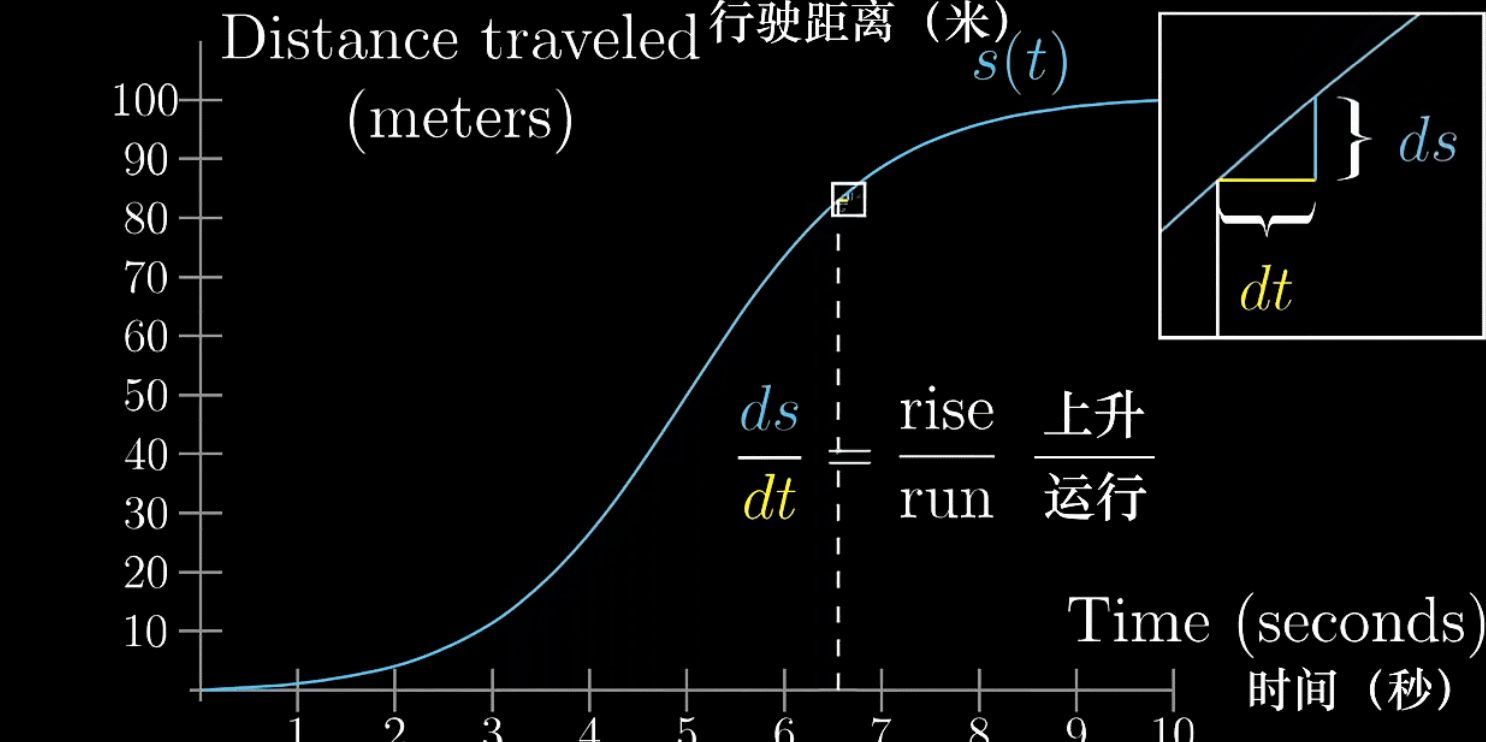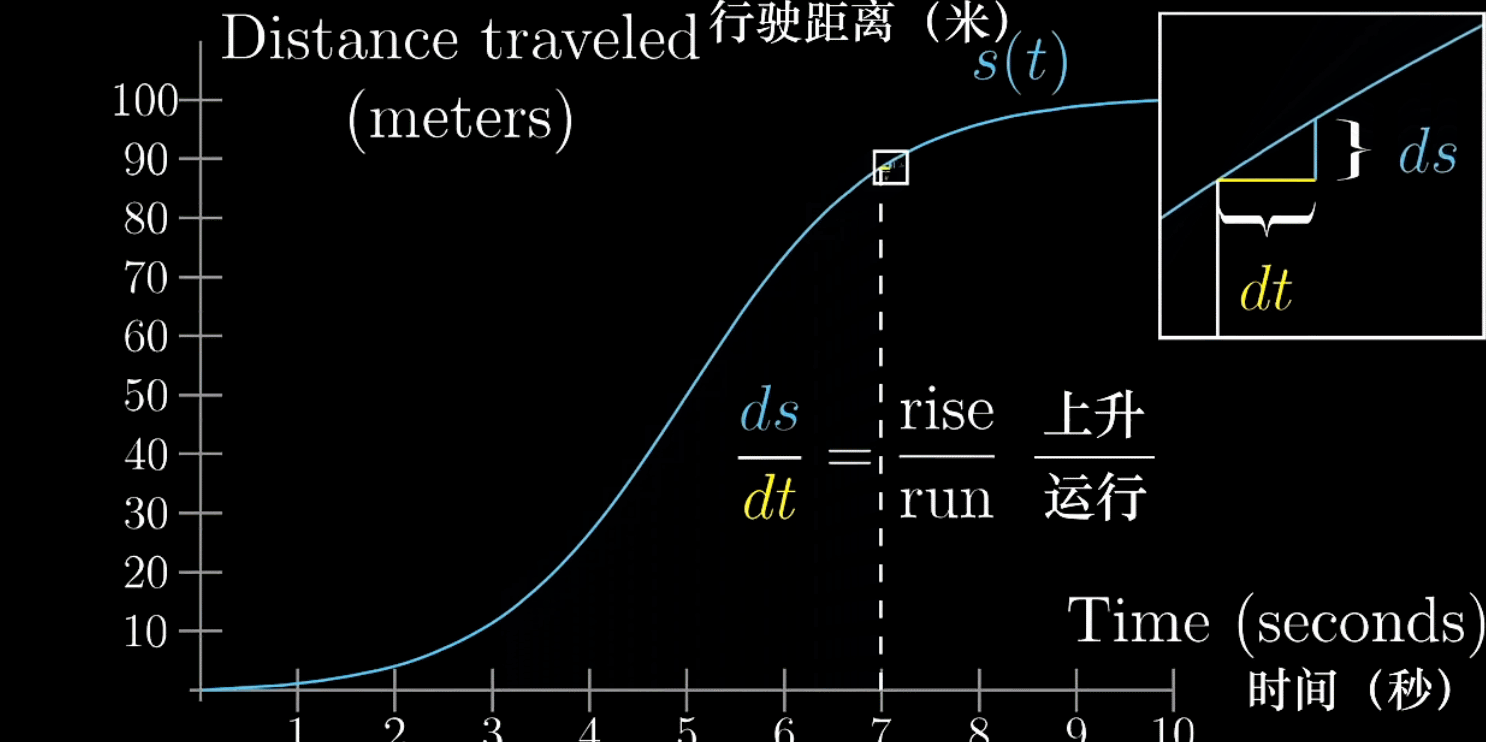
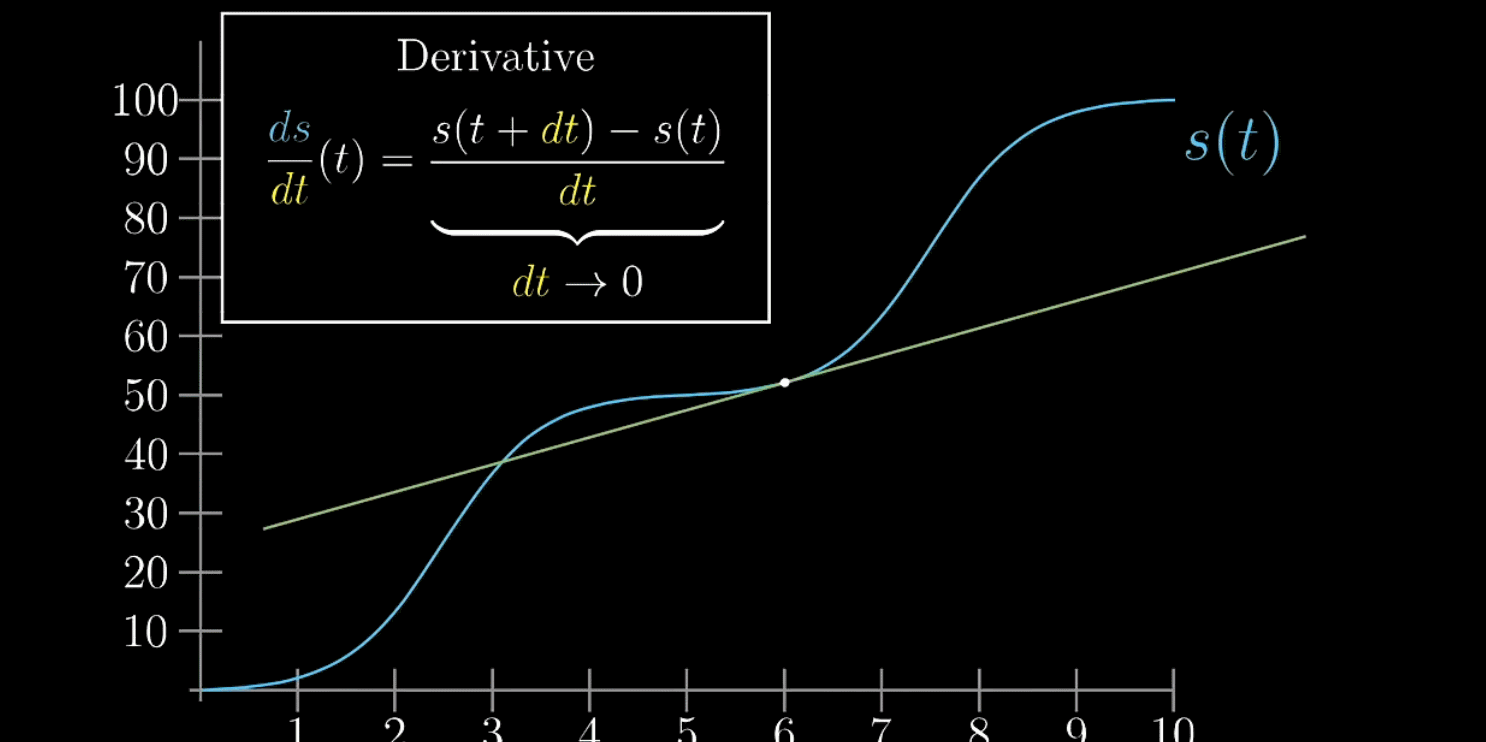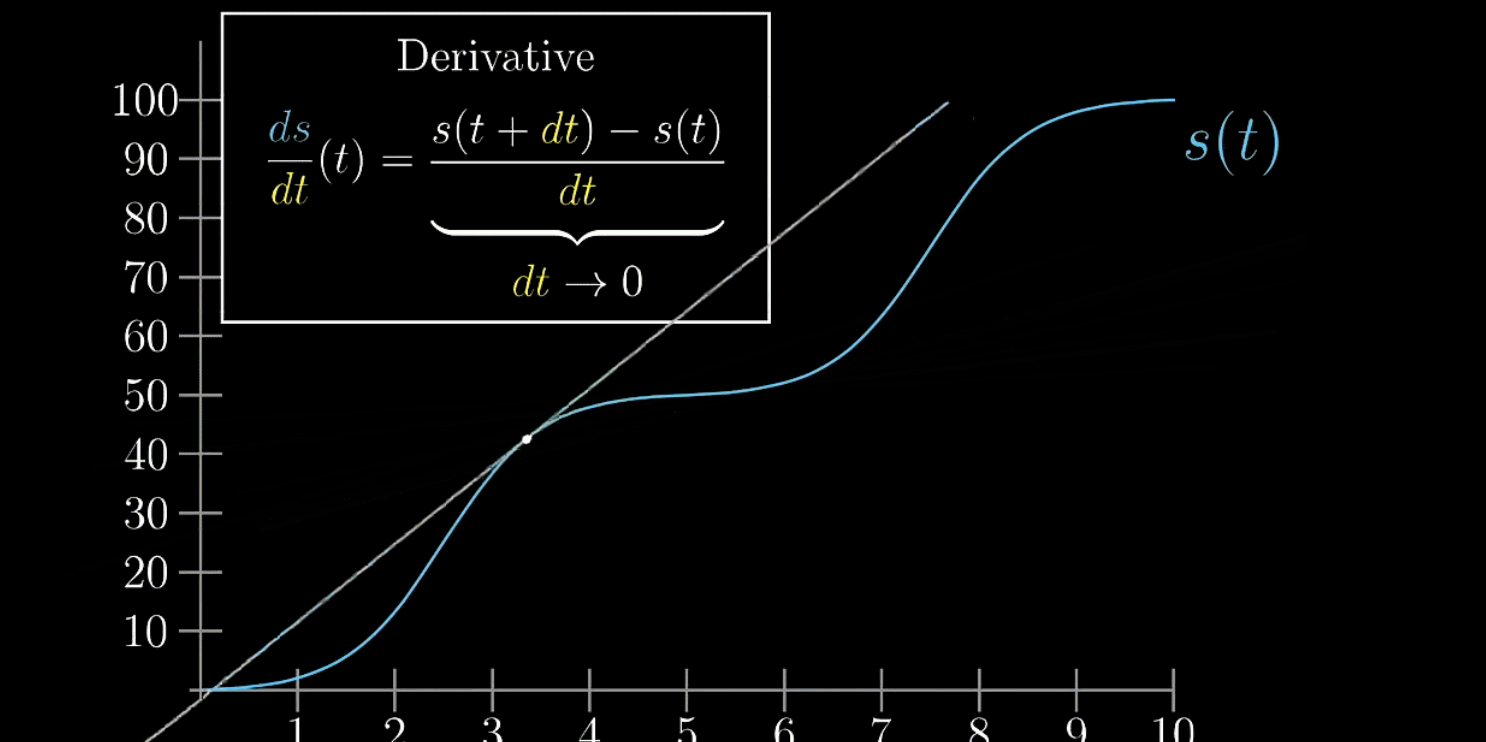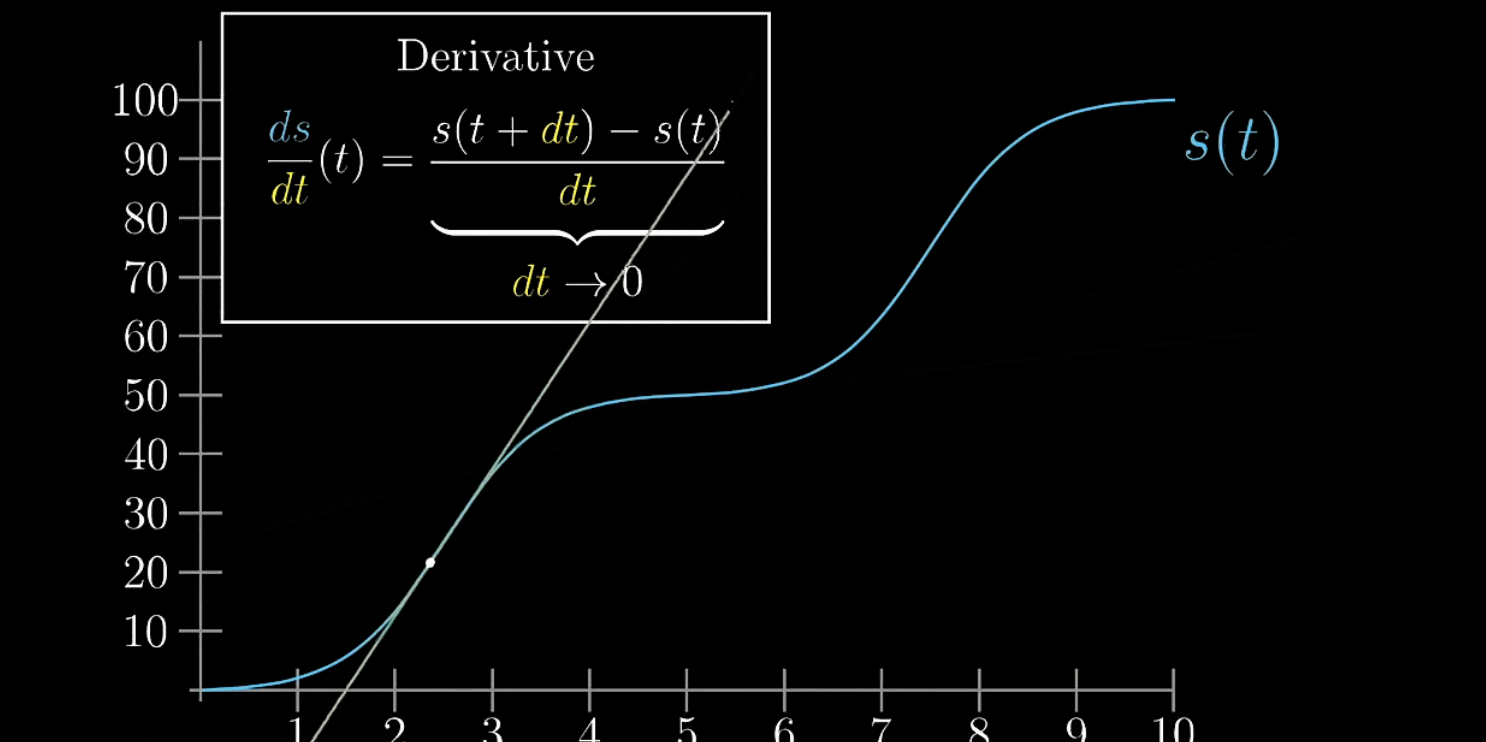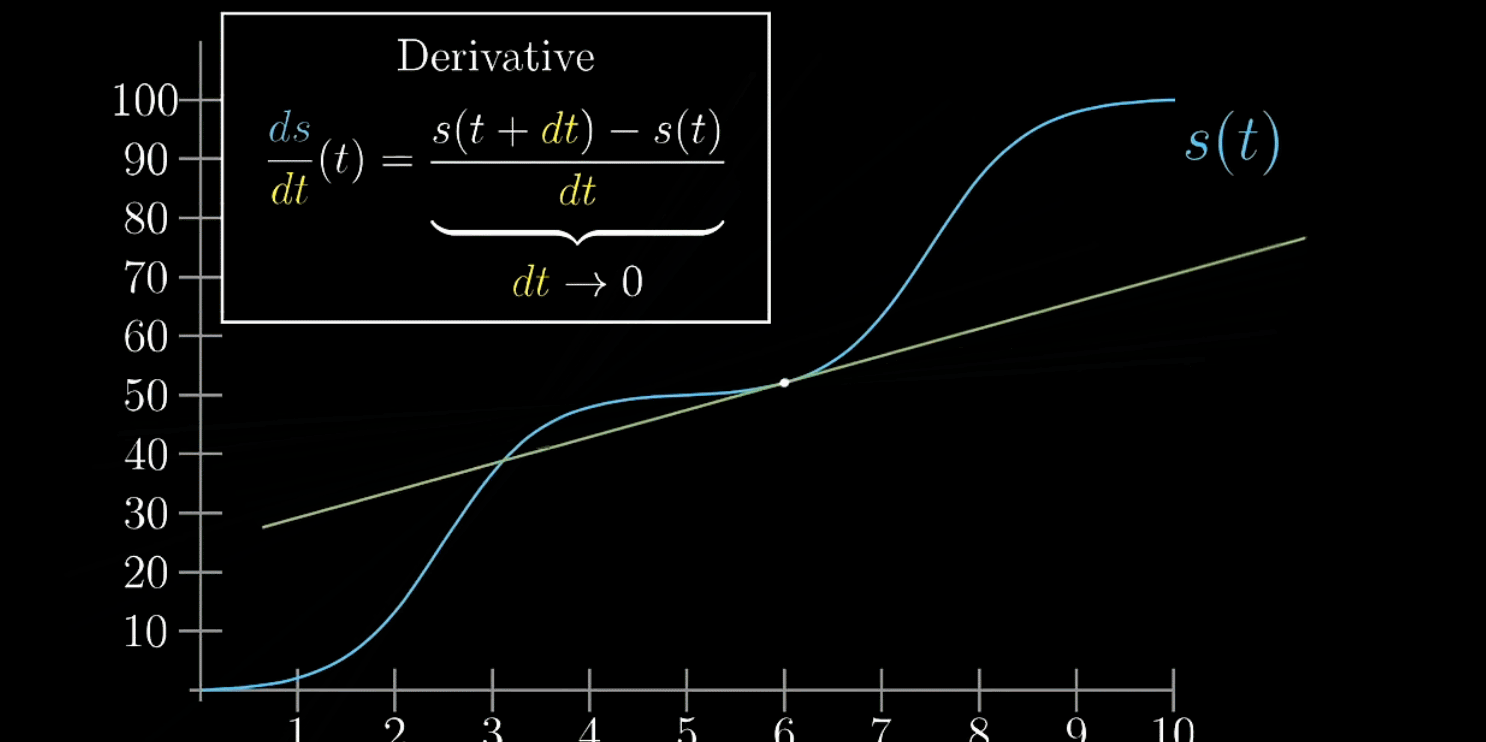
在绘制图像时,就可以给出下面的公式
随着越来越小,
趋近于切线的斜率,这才是纯数学上的导数。
不是无穷小,也不是0,是接近0的有限小量。这样想导数不是绝对瞬时,别把它看成某一点的瞬时变化率,而是当成某一点附近的变化率
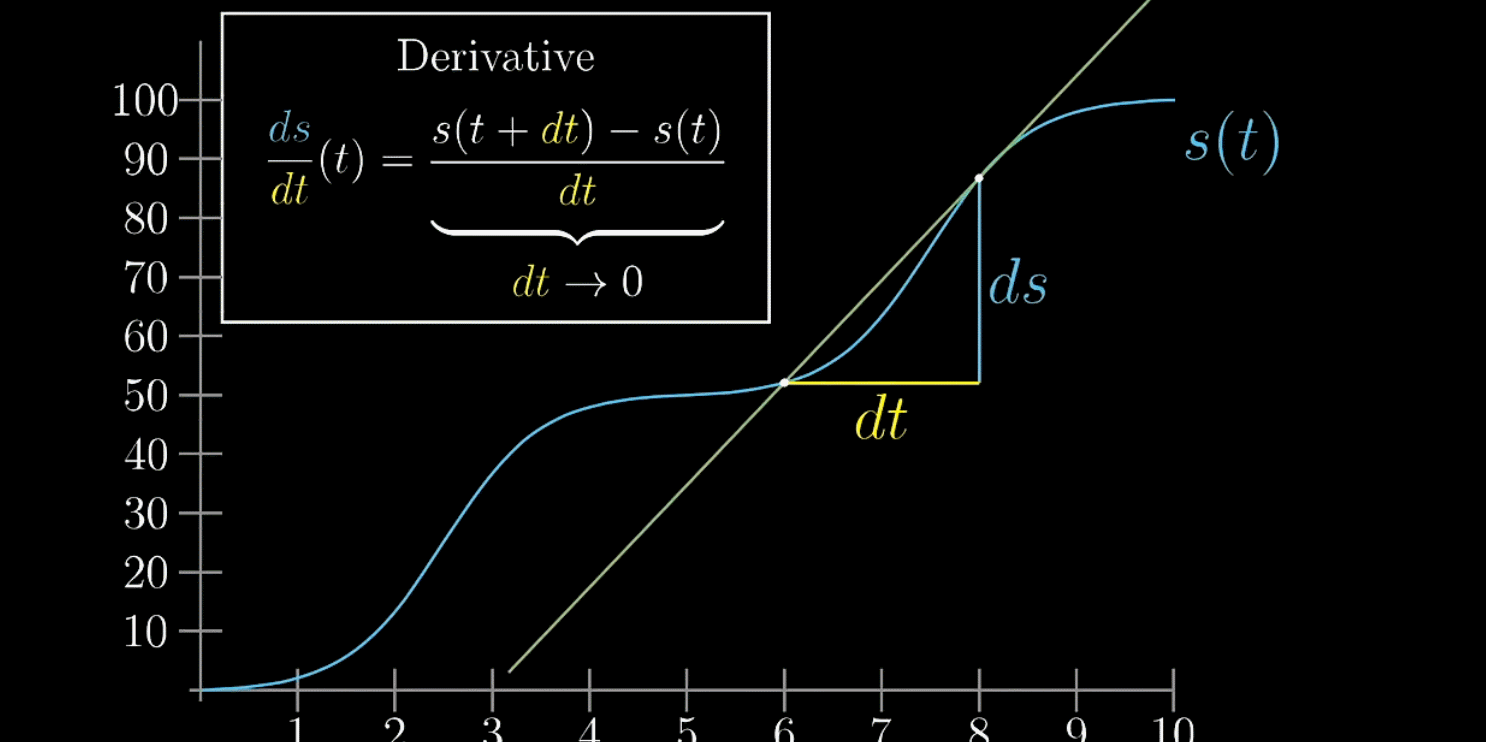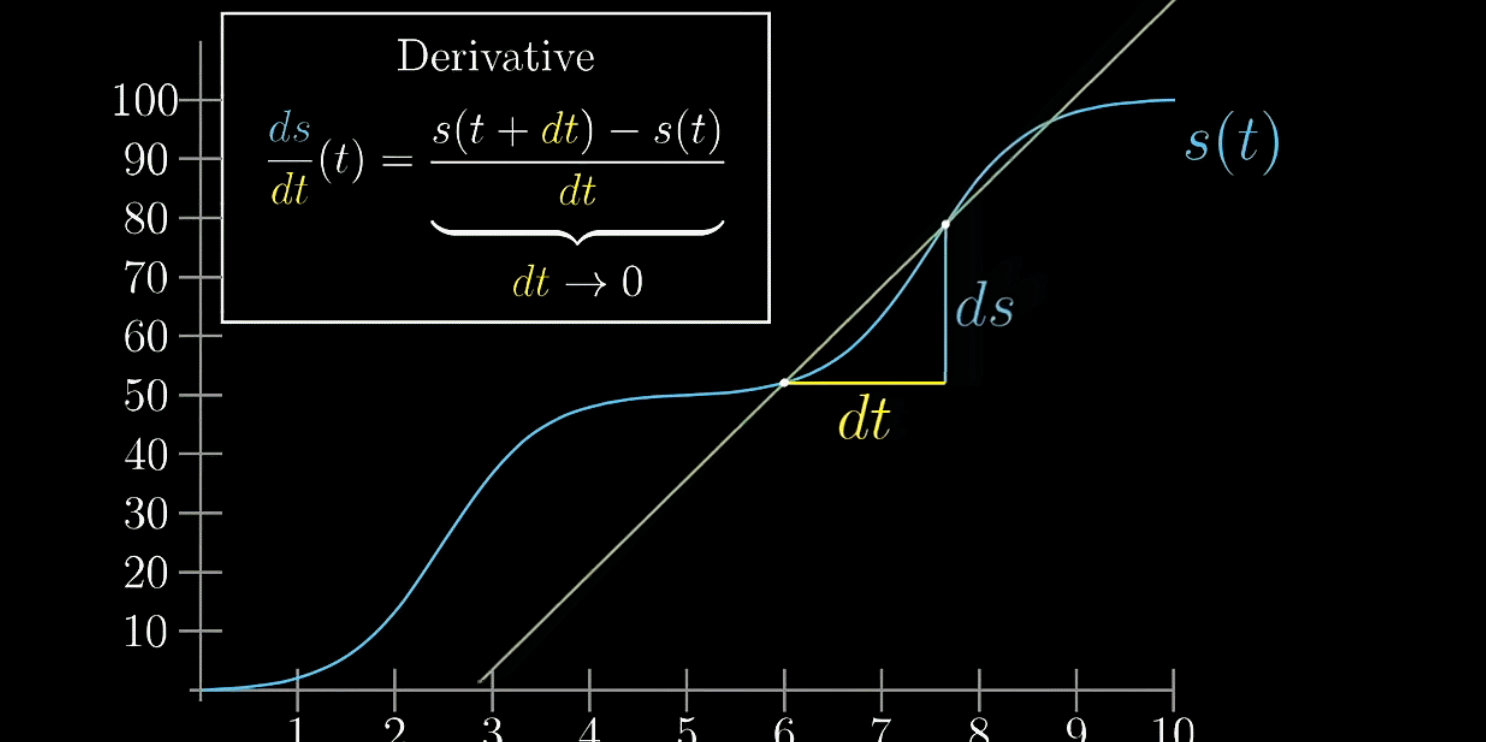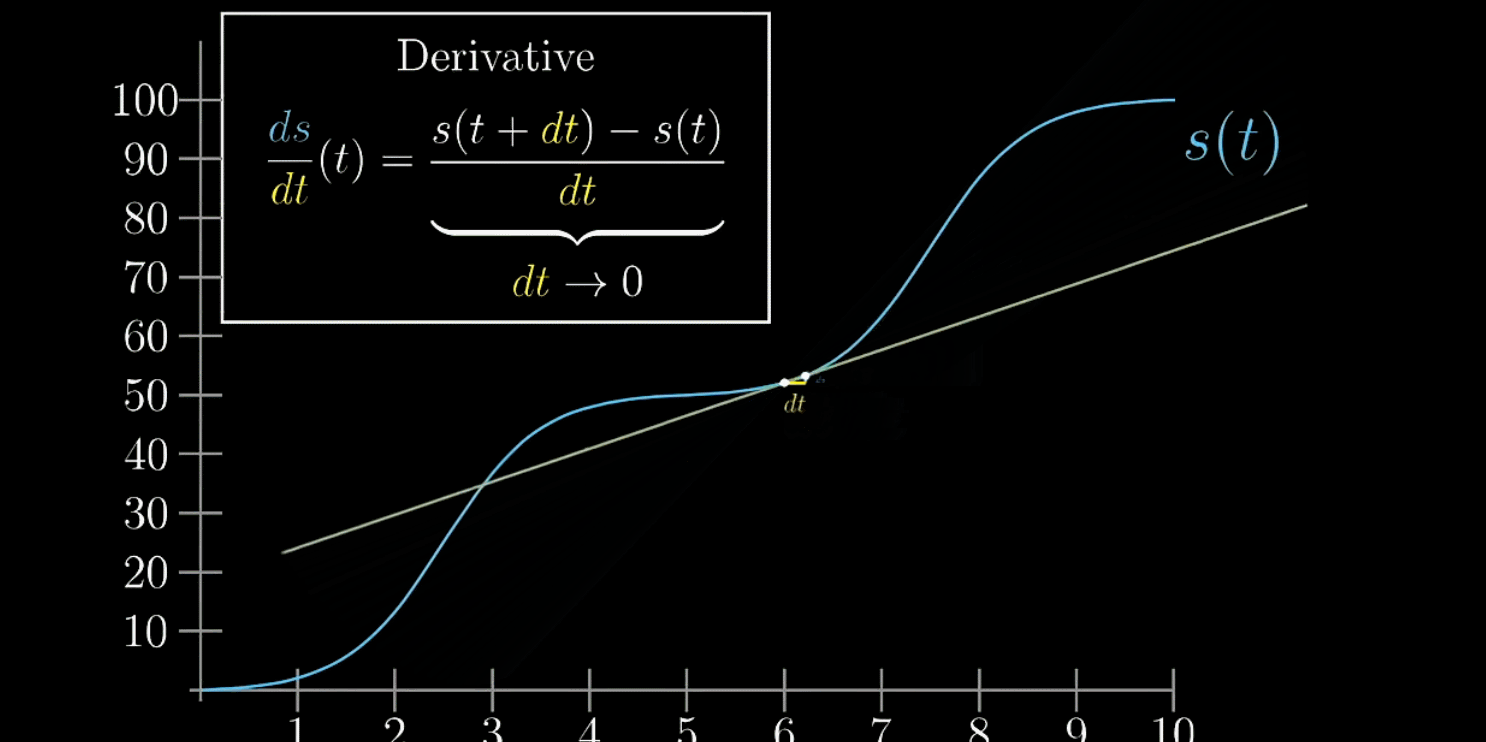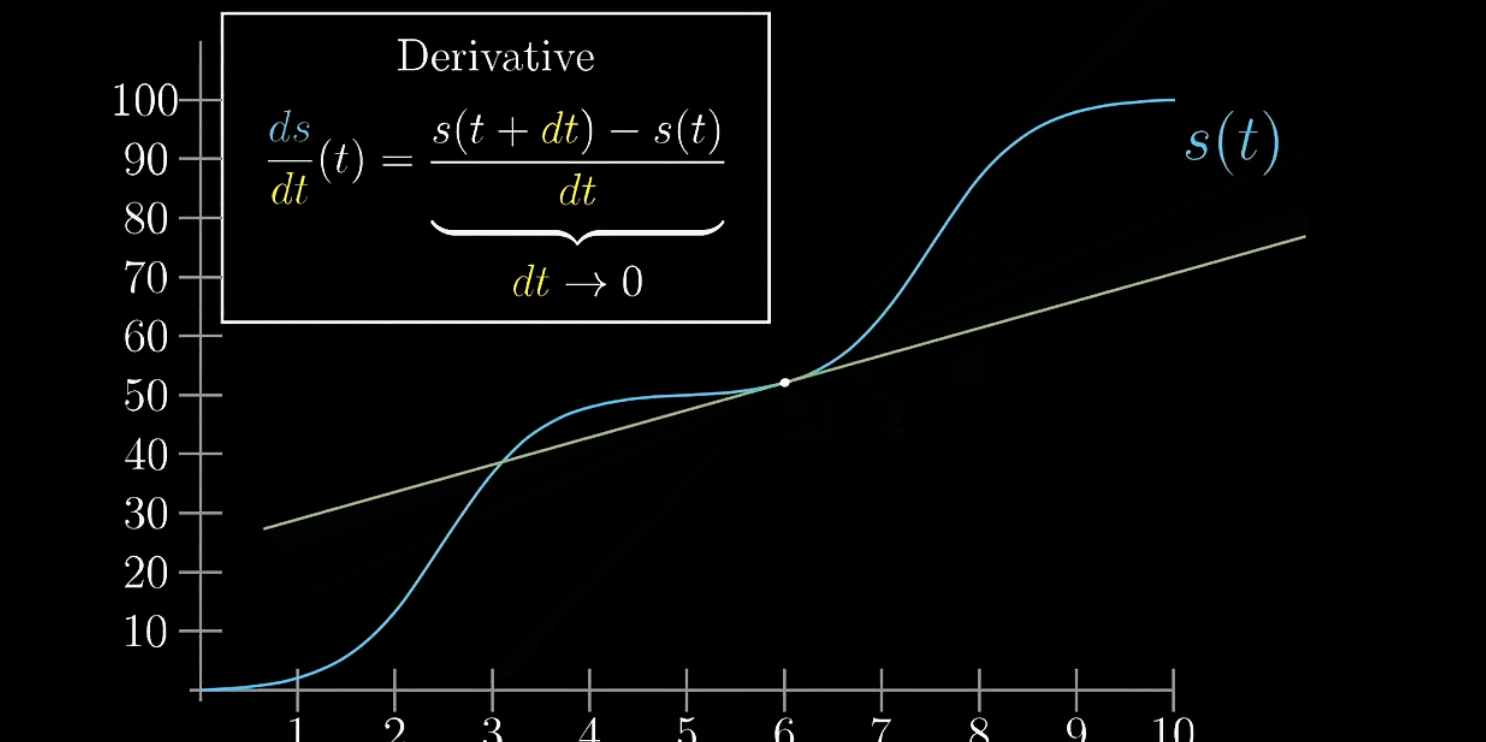
如下
(2)导数概念
定义:设函数在
的某邻域内有定义,若极限
存在,则称f(x)在点处可导,并称此极限值为
在
处的导数,记为
;如果极限不存在,那么则称
在点
处不可导
- 导数刻画了函数在某点的变化率
- 左导数:
- 右导数:
(3)可导
定理:函数在点
处可导的充分必要条件是它在该点处左导数与右导数都存在且相等
- 区间上可导及导函数:如果
在开区间(a,b)内每一点都可导,则称
在区间(a,b)内可导,此时对于(a,b)内的每一点
,都对应一个导数值
,常称
为
在(a, b)内的导函数,简称导数。若
在区间(a, b)内可导,且
和
都存在,则称
在区间[a, b]上可导
三:微分的概念
(1)微分概念
定义:如果可以表示为
,则称函数
在点
处可微,称
为微分,记为
(2)可微
定理:函数在点
处可微的充分必要条件是
在点
处可导,并且有
四:导数与微分的几何意义
导数的几何意义:导数在几何上表示曲线
在点
处切线的斜率
- 切线方程:
- 法线方程:
微分的几何意义:微分在几何上表示曲线
的切线上的增量,即
,

五:连续、可导和可微之间的关系
























