【小航的算法日记】图论

原创

wx6384c0e6d11a4 2022-11-29 10:23:51 博主文章分类：小航的算法日记 ©著作权

文章标签 算法图论最短路搜索单源最短路 文章分类 数据结构与算法人工智能

©著作权归作者所有：来自51CTO博客作者wx6384c0e6d11a4的原创作品，请联系作者获取转载授权，否则将追究法律责任

一、概念、模板

存图方式：

1.邻接矩阵

适用边数较多的稠密图（边数量 m ≈ 点数量 n² ）

// 邻接矩阵数组：w[a][b] = c 代表从 a 到 b 有权重为 c 的边
int[][] w = new int[N][N];

// 加边操作
void add(int a, int b, int c) {
    w[a][b] = c;
}

2.邻接表

使用边数较少的稀疏图（边数量 m ≈ 点数量 n）【这种存图方式又称：链式前向星存图】

int[] head = new int[N]; // 某节点对应的边
int[] edge = new int[M];  // 某条边指向的节点
int[] nextEdge = new int[M]; // 寻找下一条边 
int[] weight = new int[M]; // 边的权重
int idx; // 对边进行编号

void add(int a, int b, int c) {
    edge[idx] = b;
    nextEdge[idx] = head[a];
    head[a] = idx;
    weight[idx] = c;
    idx++;
}

遍历所有由 a 点发出的边：

for (int i = head[a]; i != -1; i = nextEdge[i]) {
    int b = edge[i], c = weight[i]; // 存在由 a 指向 b 的边，权重为 c
}

3.类

【确保某个操作复杂度严格为 O(m) 时才使用】

通过建立一个类来记录有向边信息：

class Edge {
    // 代表从 a 到 b 有一条权重为 c 的边
    int a, b, c;
    Edge(int _a, int _b, int _c) {
        a = _a; b = _b; c = _c;
    }
}

使用 List 存起所有的边对象，并在需要遍历所有边的时候，进行遍历：

List<Edge> es = new ArrayList<>();

...

for (Edge e : es) {
    ...
}

算法：

拓扑排序：

「入度」和「出度」的概念：

入度：有多少条边直接指向该节点；
出度：由该节点指出边的有多少条。

在图论中，一个有向无环图必然存在至少一个拓扑序与之对应，反之亦然。

最短路问题：

1.Floyd 「多源汇最短路」

多源汇最短路算法 Floyd 也是基于动态规划，其原始的三维状态定义为 f[i][j][k] 代表从点 i 到点 j，且经过的所有点编号不会超过 k（即可使用点编号范围为 [1, k]）的最短路径

2.朴素 Dijkstra 「单源最短路」

3.堆优化 Dijkstra 「单源最短路」

很多时候给定的图存在负权边，这时类似Dijkstra等算法没有用武之地（Dijkstra算法只能用来解决正权图的单源最短路径问题）

Bellman Ford/SPFA 都是基于动态规划，其原始的状态定义为 f[i][k] 代表从起点到 i 点，且经过最多 k 条边的最短路径。

4.Bellman Ford 「单源最短路」

优点：可以解决有负权边的单源最短路径问题，而且可以用来判断是否有负权回路，Bellman_ford算法还可以求边数限制的最短路，SPFA不能。
缺点：时间复杂度 O(N*E) (N是点数，E是边数)普遍是要高于Dijkstra算法O(N²)的

实现概述：

1.建立一个dist数组（初始化为INF，该点到他本身赋为0）记录起始点到所有点的最短路径
2.确定需要迭代的次数（可能会有边数限制），每次遍历对所有的边进行一次松弛操作，直到遍历结束。
3.遍历都结束后，若在进行一次遍历，还能得到s到某些节点更短的路径的话，则说明存在负环路。

5.SPFA「单源最短路」

SPFA 是对 Bellman Ford 的优化实现，可以使用队列进行优化，也可以使用栈进行优化。不过该算法的稳定性较差，在稠密图中SPFA算法时间复杂度会退化。

实现概述：

1.建立一个队列，初始时队列只有一个起始点，建立一个dist数组（初始化INF，该点到他本身赋为0）记录起始点到所有点的最短路径
2.松弛操作：用队列的点刷新起始点到所有点的最短路，如果刷新成功，且该点不在队列加入队列，直到队列为空

图解：

给定一个有向图，求A~E的最短路。

【小航的算法日记】图论_算法

源点A首先入队，并且AB松弛

【小航的算法日记】图论_搜索_02

扩展与A相连的边，B，C 入队并松弛

【小航的算法日记】图论_最短路_03

B，C分别开始扩展，D入队并松弛

【小航的算法日记】图论_搜索_04

D出队，E入队并松弛。

【小航的算法日记】图论_搜索_05

E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

【小航的算法日记】图论_最短路_06

最小生成树：

1.Kruskal

多源BFS：

男たちはグランドラインを目指し（めざし）梦を（ゆめを）追い（おい）続ける（つづける）。世はまさに大海贼时代（じだい）。
于是男子汉们起程前往伟大的航路，追逐梦想，大海贼时代来临了。

一般，广度优先搜索都是从一个源点出发。

【小航的算法日记】图论_图论_07

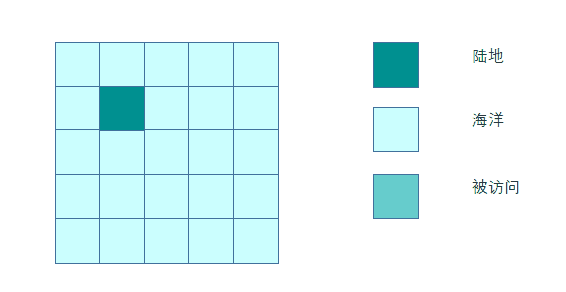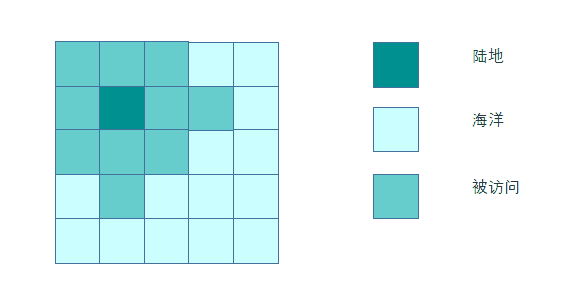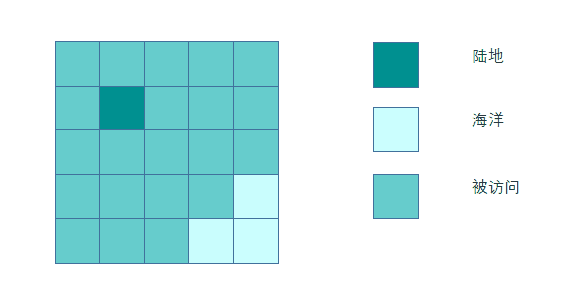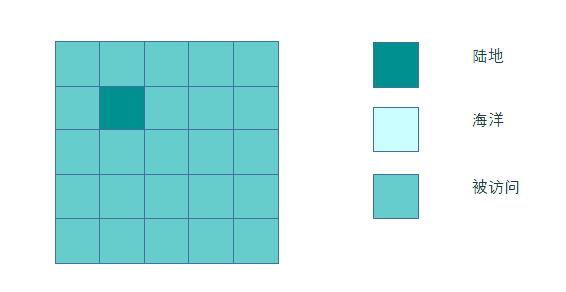
多源广度优先搜索长这样。

【小航的算法日记】图论_图论_08

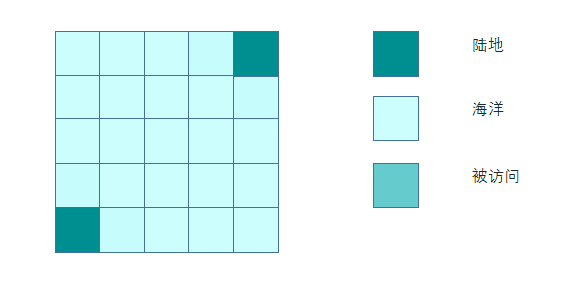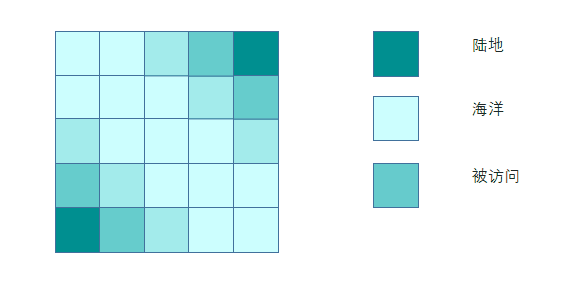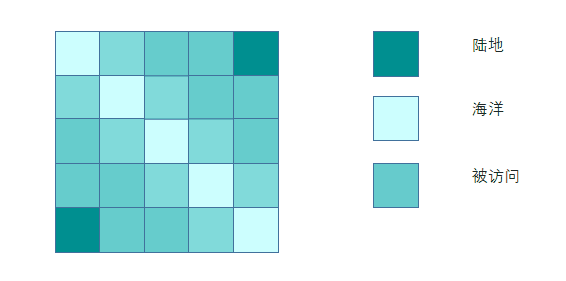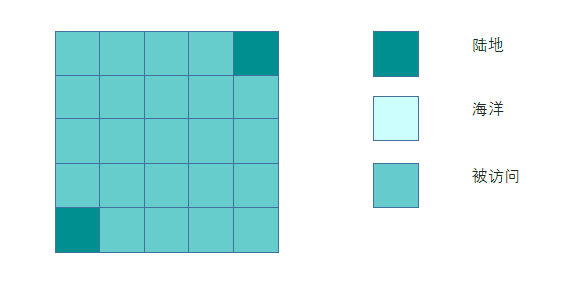
如何证明理解多源点BFS的正确性？其实可以通过添加超级源点方式来思考。添加超级源点可以使多源BFS退化成单源BFS。

首先让我们用离散数学中图的概念来描述这张地图：

海洋和陆地都是图中的结点。
相邻网格的对应结点之间有一条无向边。

这样地图中的网格及其相邻关系构成了一张无向无权图。如下图示：

【小航的算法日记】图论_单源最短路_09

我们向图中加入一个超级源点，并在超级源点与每个陆地结点之间建立一条边。如下图示：

【小航的算法日记】图论_算法_10

现在我们从超级源点开始做单源BFS，发现原先的多个源点只不过是BFS的第二层而已~。

所以多源BFS没有改变BFS的本质，不会影响结果的正确性~

双向BFS：

实现思路：

创建「两个队列」分别用于两个方向的搜索；
创建「两个哈希表」用于「解决相同节点重复搜索」和「记录转换次数」；
为了尽可能让两个搜索方向“平均”，每次从队列中取值进行扩展时，先判断哪个队列容量较少；
如果在搜索过程中「搜索到对方搜索过的节点」，说明找到了最短路径。

伪代码：

// q1、q2 为两个方向的队列
// m1、m2 为两个方向的哈希表，记录每个节点距离起点的
    
// 只有两个队列都不空，才有必要继续往下搜索
// 如果其中一个队列空了，说明从某个方向搜到底都搜不到该方向的目标节点，反向搜索也没必要进行了
while(!q1.isEmpty() && !q2.isEmpty()) {
    if (q1.size() <= q2.size()) {
        update(q1, m1, m2);
    } else {
        update(q2, m2, m1);
    }
}

// update 为将当前队列 q 中包含的元素取出，进行「一次完整扩展」的逻辑（按层拓展）
void update(Queue q, Map cur, Map other) {}

二、例题

多源BFS

题：417. 太平洋大西洋水流问题

有一个 m × n 的矩形岛屿，与太平洋和大西洋相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格高于海平面的高度。

岛上雨水较多，如果相邻单元格的高度小于或等于当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表，其中 result[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 流动既可流向太平洋也可流向大西洋。

示例 1：

【小航的算法日记】图论_图论_11

输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 105

解：

解题思路：由四周向中心BFS，取交集

AC代码：

class Solution {
    int n, m;
    int[][] g;
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        g = heights;
        m = heights.length; n = g[0].length;
        Queue<int[]> q1 = new LinkedList<>(), q2 = new LinkedList<>();
        boolean[][] res1 = new boolean[m][n], res2 = new boolean[m][n];
        // 初始化访问队列
        for(int i = 0; i < m; ++ i) {
            for(int j = 0; j < n; ++ j) {
                // 左上角
                if(i == 0 || j == 0) {
                    res1[i][j] = true;
                    q1.offer(new int[]{i ,j});
                }
                // 右下角
                if(i == m - 1 || j == n - 1) {
                    res2[i][j] = true;
                    q2.offer(new int[]{i, j});
                }
            }
        }
        // BFS
        bfs(q1, res1); bfs(q2, res2);
        // 取res1, res2的交集
        List<List<Integer>> ans = new ArrayList<>();
        for(int i = 0; i < m; ++ i) {
            for(int j = 0; j < n; ++ j) {
                if(res1[i][j] && res2[i][j]) {
                    ans.add(new ArrayList<Integer>(Arrays.asList(i, j)));
                }
            }
        }
        return ans;
    }
    int[][] dirs = new int[][] {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    void bfs(Queue<int[]> q, boolean[][] res) {
        while(!q.isEmpty()) {
            int[] info = q.poll();
            int x = info[0], y = info[1], w = g[x][y];
            for(int[] dir : dirs) {
                int nx = x + dir[0], ny = y + dir[1];
                // 向高处拓展
                if(isMap(nx, ny) && !res[nx][ny] && w <= g[nx][ny]) {
                    q.offer(new int[] {nx, ny});
                    res[nx][ny] = true;
                }
            }
        }
    }
    boolean isMap(int x, int y) {
        return x >= 0 && x < m && y >= 0 && y < n;
    }
}

解题思路：DFS

AC代码：

class Solution {
    int n, m;
    int[][] g;
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        m = heights.length; n = heights[0].length;
        g = heights;
        boolean[][] res1 = new boolean[m][n], res2 = new boolean[m][n];
        // 初始化
        for(int i = 0; i < m; ++ i) {
            for(int j = 0; j < n; ++ j) {
                if(i == 0 || j == 0) {
                    if(!res1[i][j]) dfs(i, j, res1);
                }
                if(i == m - 1 || j == n - 1) {
                    if(!res2[i][j]) dfs(i, j, res2);
                }
            }
        }
        List<List<Integer>> ans = new ArrayList<>();
        for(int i = 0; i < m; ++ i) {
            for(int j = 0; j < n; ++ j) {
                if(res1[i][j] && res2[i][j]) {
                    ans.add(new ArrayList<Integer>(Arrays.asList(i, j)));
                }
            }
        }
        return ans;
    }
    int[][] dirs = new int[][] {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
    void dfs(int x, int y, boolean[][] res) {
        res[x][y] = true;
        for(int[] dir : dirs) {
            int dx = x + dir[0], dy = y + dir[1];
            if(isMap(dx, dy) && !res[dx][dy] && g[dx][dy] >= g[x][y]) {
                dfs(dx, dy, res);
            }
        }
    }
    boolean isMap(int x, int y) {
        return x >= 0 && x < m && y >= 0 && y < n;
    }
}

解题思路：并查集

AC代码：

class Solution {
    int N = 200 * 200 + 10;
    int[] p1 = new int[N], p2 = new int[N];
    int n, m, tot, S, T;
    int[][] g;
    void union(int[] p, int a, int b) {
        p[find(p, a)] = p[find(p, b)];
    }
    int find(int[] p, int x) {
        if (p[x] != x) p[x] = find(p, p[x]);
        return p[x];
    }
    boolean query(int[] p, int a, int b) {
        return find(p, a) == find(p, b);
    }
    int getIdx(int x, int y) {
        return x * n + y;
    }
    public List<List<Integer>> pacificAtlantic(int[][] _g) {
        g = _g;
        m = g.length; n = g[0].length; tot = m * n; S = tot + 1; T = tot + 2;
        for (int i = 0; i <= T; i++) p1[i] = p2[i] = i;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int idx = getIdx(i, j);
                if (i == 0 || j == 0) {
                    if (!query(p1, S, idx)) dfs(p1, S, i, j);
                }
                if (i == m - 1 || j == n - 1) {
                    if (!query(p2, T, idx)) dfs(p2, T, i, j);
                }
            }
        }
        List<List<Integer>> ans = new ArrayList<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int idx = getIdx(i, j);
                if (query(p1, S, idx) && query(p2, T, idx)) {
                    List<Integer> list = new ArrayList<>();
                    list.add(i); list.add(j);
                    ans.add(list);
                }
            }
        }
        return ans;
    }
    int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
    void dfs(int[] p, int ori, int x, int y) {
        union(p, ori, getIdx(x, y));
        for (int[] di : dirs) {
            int nx = x + di[0], ny = y + di[1];
            if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
            if (query(p, ori, getIdx(nx, ny)) || g[nx][ny] < g[x][y]) continue;
            dfs(p, ori, nx, ny);
        }
    }
}

题：1162. 地图分析

你现在手里有一份大小为 n x n 的网格 grid，上面的每个单元格都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

【小航的算法日记】图论_搜索_12

输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

【小航的算法日记】图论_算法_13

输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

提示：

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 不是 0 就是 1

解：

解题思路：

为了方便，我们在使用哈希表记录距离时，将二维坐标 (x, y) 转化为对应的一维下标 idx = x * n + y 作为 key 进行存储

多源BFS扩散的图示：（1表示陆地，0表示海洋）

【小航的算法日记】图论_图论_14

AC代码：

class Solution {
    // 0-海洋，1-陆地
    public int maxDistance(int[][] grid) {
        int n = grid.length;
        Queue<int[]> queue = new LinkedList<>();
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < n; ++ i) {
            for(int j = 0; j < n; ++ j) {
                if(grid[i][j] == 1) {
                    queue.offer(new int[] {i, j});
                    map.put(i * n + j, 0);
                }
            }
        }
        int ans = -1;
        int[][] dirs = new int[][] {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
        while(!queue.isEmpty()) {
            int[] poll = queue.poll();
            int dx = poll[0], dy = poll[1];
            int step = map.get(dx * n + dy);
            for(int[] dir : dirs) {
                int nx = dx + dir[0], ny = dy + dir[1];
                // 在这块岛屿并且是海洋
                if(isMap(nx, ny, n) && grid[nx][ny] == 0) {
                    grid[nx][ny] = step + 1;
                    queue.offer(new int[] {nx, ny});
                    map.put(nx * n + ny, step + 1);
                    ans = Math.max(ans, step + 1);
                }
            }
        }
        return ans;
    }
    boolean isMap(int x, int y, int n) {
        return x >= 0 && x < n && y >= 0 && y < n;
    }
}

双向BFS

题：433. 最小基因变化

基因序列可以表示为一条由 8 个字符组成的字符串，其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。

假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。

例如，"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。

另有一个基因库 bank 记录了所有有效的基因变化，只有基因库中的基因才是有效的基因序列。（变化后的基因必须位于基因库 bank 中）

给你两个基因序列 start 和 end ，以及一个基因库 bank ，请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化，返回 -1 。

注意：起始基因序列 start 默认是有效的，但是它并不一定会出现在基因库中。

示例 1：

输入：start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出：1

示例 2：

输入：start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出：2

示例 3：

输入：start = "AAAAACCC", end = "AACCCCCC", bank =   ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出：3

提示：

start.length == 8
end.length == 8
0 <= bank.length <= 10
bank[i].length == 8
start、end 和 bank[i] 仅由字符 ['A', 'C', 'G', 'T'] 组成

解：

解题思路：双向BFS

AC代码：

class Solution {
    static char[] items = new char[] {'A', 'C', 'G', 'T'};
    Set<String> set = new HashSet<>();
    public int minMutation(String start, String end, String[] bank) {
        set.add(start);
        for(String s : bank) set.add(s);
        // 变化后的基因必须位于基因库 bank 中
        if(!set.contains(end)) return -1;
        Queue<String> q1 = new LinkedList<>(), q2 = new LinkedList<>();
        q1.offer(start); q2.offer(end);
        Map<String, Integer> m1 = new HashMap<>(), m2 = new HashMap<>();
        m1.put(start, 0); m2.put(end, 0);
        while(!q1.isEmpty() && !q2.isEmpty()) {
            int t = -1;
            if(q1.size() <= q2.size()) t = update(q1, m1, m2);
            else t = update(q2, m2, m1);
            if(t != -1) return t;
        }
        return -1;
    }
    int update(Queue<String> q, Map<String, Integer> cur, Map<String, Integer> other) {
        int m = q.size();
        while(m -- > 0) {
            String s = q.poll();
            char[] cs = s.toCharArray();
            int step = cur.get(s);
            // 基因序列可以表示为一条由 8 个字符组成的字符串
            for(int i = 0; i < 8; ++ i) {
                for(char item : items) {
                    char[] clone = cs.clone();
                    clone[i] = item;
                    String newStr = String.valueOf(clone);
                    if(!set.contains(newStr) || cur.containsKey(newStr)) continue;
                    if(other.containsKey(newStr)) return other.get(newStr) + step + 1;
                    q.offer(newStr);
                    cur.put(newStr, step + 1);
                }
            }
        }
        return -1;
    }
}

题：752. 打开转盘锁

你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字： '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转：例如把 ‘9’ 变为 ‘0’，‘0’ 变为 ‘9’ 。每次旋转都只能旋转一个拨轮的一位数字。

锁的初始数字为 '0000' ，一个代表四个拨轮的数字的字符串。

列表 deadends 包含了一组死亡数字，一旦拨轮的数字和列表里的任何一个元素相同，这个锁将会被永久锁定，无法再被旋转。

字符串 target 代表可以解锁的数字，你需要给出解锁需要的最小旋转次数，如果无论如何不能解锁，返回 -1 。

示例 1:

输入：deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出：6
解释：
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的，
因为当拨动到 "0102" 时这个锁就会被锁定。

示例 2:

输入: deadends = ["8888"], target = "0009"
输出：1
解释：把最后一位反向旋转一次即可 "0000" -> "0009"。

示例 3:

输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出：-1
解释：无法旋转到目标数字且不被锁定。

提示：

1 <= deadends.length <= 500
deadends[i].length == 4
target.length == 4
target 不在 deadends 之中
target 和 deadends[i] 仅由若干位数字组成

解：

解题思路：双向BFS

AC代码：

class Solution {
    Set<String> set = new HashSet<>();
    public int openLock(String[] deadends, String end) {
        String start = "0000";
        if(start.equals(end)) return 0;
        // 判断是否存在于某集合中
        for(String d : deadends) set.add(d);
        if(set.contains(start)) return -1;
        // 双向BFS
        Queue<String> q1 = new LinkedList<>(), q2 = new LinkedList<>();
        HashMap<String, Integer> m1 = new HashMap<>(), m2 = new HashMap<>();
        q1.offer(start); q2.offer(end);
        m1.put(start, 0); m2.put(end, 0);
        while(!q1.isEmpty() && !q2.isEmpty()) {
            int t = -1;
            if(q1.size() <= q2.size()) t = update(q1, m1, m2);
            else t = update(q2, m2, m1);
            if(t != -1) return t;
        }
        return -1;
    }
    int[] dirs = new int[] {1, -1}; // 1 ：正向转，-1 ：反向转
    int update(Queue<String> q, Map<String, Integer> cur, Map<String, Integer> other) {
        int m = q.size();
        while(m -- > 0) {
            String poll = q.poll();
            char[] pcs = poll.toCharArray();
            int step = cur.get(poll);
            // 每个字符串共有四个字符
            for(int i = 0; i < 4; ++ i) {
                // 遍历方向
                for(int dir : dirs) {
                    // 替换字符串
                    int next = (pcs[i] - '0' + dir + 10) % 10;
                    char[] clone = pcs.clone();
                    clone[i] = (char)(next + '0');
                    String str = String.valueOf(clone);
                    if(set.contains(str) || cur.containsKey(str)) continue;
                    if(other.containsKey(str)) return step + 1 + other.get(str);
                    q.offer(str);
                    cur.put(str, step + 1);
                }
            }
        }
        return -1;
    }
}

拓扑排序

题：207. 课程表

你这个学期必须选修 numCourses 门课程，记为0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

1 <= numCourses <= 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同

解：

解题思路：

1.存图：若存在前置课程，寸边，并统计所有的点入度
2.创建队列，将入度为0的点加入队列
3.拓扑排序，若所有点都被访问，则所有课程都能访问，

AC代码：

class Solution {
    // 邻接表
    int N = 100010, M = 5010;
    int[] head = new int[N], edge = new int[M], nextEdge = new int[M];
    int idx;
    int[] count = new int[N]; // 统计点的入度
    void add(int a, int b) {
        edge[idx] = b;
        nextEdge[idx] = head[a];
        head[a] = idx;
        idx ++;
        count[b] ++; 
    } 
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        Arrays.fill(head, -1);
        for(int[] info : prerequisites) add(info[1], info[0]);
        int ans = 0;
        Queue<Integer> queue = new LinkedList<>();
        for(int i = 0; i < numCourses; ++ i) {
            if(count[i] == 0) queue.offer(i); // 将没有先行课的先加入队列
        }
        while(!queue.isEmpty()) {
            int t = queue.poll();
            ans ++;
            for(int i = head[t]; i != -1; i = nextEdge[i]) {
                int j = edge[i];
                if(-- count[j] == 0) queue.offer(j); // 将没有的课加入队列继续遍历
            }
        }
        return ans == numCourses;
    }
}

题：802. 找到最终的安全状态

有一个有 n 个节点的有向图，节点按 0 到 n - 1 编号。图由一个索引从 0 开始的 2D 整数数组 graph表示， graph[i]是与节点 i 相邻的节点的整数数组，这意味着从节点 i 到 graph[i]中的每个节点都有一条边。

如果一个节点没有连出的有向边，则它是 终端节点 。如果没有出边，则节点为终端节点。如果从该节点开始的所有可能路径都通向 终端节点 ，则该节点为 安全节点 。

返回一个由图中所有 安全节点 组成的数组作为答案。答案数组中的元素应当按升序排列。

示例 1：

【小航的算法日记】图论_单源最短路_15

输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]
解释：示意图如上。
节点 5 和节点 6 是终端节点，因为它们都没有出边。
从节点 2、4、5 和 6 开始的所有路径都指向节点 5 或 6 。

示例 2：

输入：graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出：[4]
解释:
只有节点 4 是终端节点，从节点 4 开始的所有路径都通向节点 4 。

提示：

n == graph.length
1 <= n <= 104
0 <= graph[i].length <= n
0 <= graph[i][j] <= n - 1
graph[i] 按严格递增顺序排列。
图中可能包含自环。
图中边的数目在范围 [1, 4 * 104] 内。

解：

解题思路：反向图 + 拓扑排序

安全序列：对于一个起始节点，如果从该节点出发，无论每一步选择沿哪条有向边行走，最后必然在有限步内到达终点，则将该起始节点称作是安全的。 => 某个点所有的出路没有回路

原图的出度为0的点 => 反向图的入度为0的点

AC代码：

class Solution {
    int N = (int)1e4+10, M = 4 * N;
    int idx;
    int[] he = new int[N], e = new int[M], ne = new int[M];
    int[] cnts = new int[N];
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = he[a];
        he[a] = idx++;
    }
    public List<Integer> eventualSafeNodes(int[][] g) {
        int n = g.length;
        // 存反向图，并统计入度
        Arrays.fill(he, -1);
        for (int i = 0; i < n; i++) {
            for (int j : g[i]) {
                add(j, i);
                cnts[i]++;
            }
        }
        // BFS 求反向图拓扑排序
        Deque<Integer> d = new ArrayDeque<>();
        for (int i = 0; i < n; i++) {
            if (cnts[i] == 0) d.addLast(i);
        }
        while (!d.isEmpty()) {
            int poll = d.pollFirst();
            for (int i = he[poll]; i != -1; i = ne[i]) {
                int j = e[i];
                if (--cnts[j] == 0) d.addLast(j);
            }
        }
        // 遍历答案：如果某个节点出现在拓扑序列，说明其进入过队列，说明其入度为 0
        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (cnts[i] == 0) ans.add(i);
        }
        return ans;
    }
}

最短路

题：743. 网络延迟时间

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过有向边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

示例 1：

【小航的算法日记】图论_搜索_16

输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2

示例 2：

输入：times = [[1,2,1]], n = 2, k = 1
输出：1

示例 3：

输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

提示：

1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
所有 (ui, vi) 对都 互不相同（即，不含重复边）

解：

此题只告诉了出发点，需要到达所有点 => 最后for循环遍历取最大

解题思路：Floyd

枚举从任意点出发，到达任意点的距离

AC代码：

class Solution {
    int N = 105, M = 6005;
    int[][] w = new int[N][N]; // 邻接矩阵
    int INF = 0x3f3f3f3f;
    int n, k;
    public int networkDelayTime(int[][] times, int _n, int _k) {
        n = _n; k = _k;
        // 初始化邻接矩阵
        for(int i = 1; i <= n; ++ i) {
            for(int j = 1; j <= n; ++ j) {
                w[i][j] = w[j][i] = i == j ? 0 : INF;
            }
        }
        // 存图
        for(int[] t : times) {
            int u = t[0], v = t[1], c = t[2];
            w[u][v] = c;
        }
        // 最短路
        floyd();
        // 遍历答案
        int ans = 0;
        for(int i = 1; i <= n; ++ i) {
            ans = Math.max(ans, w[k][i]);
        }
        return ans >= INF / 2 ? -1 : ans;
    }
    void floyd() {
        // 枚举中转点 - 枚举起点 - 枚举终点 - 松弛操作
        for(int p = 1; p <= n; ++ p) {
            for(int i = 1; i <= n; ++ i) {
                for(int j = 1; j <= n; ++ j) {
                    w[i][j] = Math.min(w[i][j], w[i][p] + w[p][j]);
                }
            }
        }
    }
}

解题思路：朴素 Dijkstra

AC代码：

class Solution {
    int N = 105, M = 6005;
    // 邻接矩阵
    int[][] w = new int[N][N];
    // 源点到x的最短距离y dist[x] = y;
    int[] dist = new int[N];
    // 标记哪些点已经被访问过
    boolean[] visited = new boolean[N];
    int INF = 0x3f3f3f3f;
    int n, k;
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; _k = k;
        // 初始化邻接矩阵
        for(int i = 1; i <= n; ++ i) {
            for(int j = 1; j <= n; ++ j) {
                w[i][j] = w[j][i] = i == j ? 0 : INF;
            }
        }
        // 存图
        for(int[] t : ts) {
            int u = t[0], v = t[1], c = t[2];
            w[u][v] = c;
        }
        // 最短路
        dijkstra();
        // 遍历取最大
        int ans = 0;
        for(int i = 1; i <= n; ++ i) {
            ans = Math.max(ans, dist[i]);
        }
        return ans > INF / 2 ? -1 : ans;
    }
    // 最短路
    void dijkstra() {
        // 初始化所有点标记，和距离数组
        Arrays.fill(dist, INF); // 源点与任何点（除自己）不可达
        dist[k] = 0;
        Arrays.fill(visited, false); // 都未访问过
        for(int p = 1; p <= n; ++ i) {
            // 找一个没见过的，距离当前点最近的下标
            int t = -1;
            for(int i = 1; i <= n; ++ i) {
                if(!visited[i] && (t == -1 || dist[i] < dist[t])) t = i;
            }
            // 标记更新
            visited[t] = true;
            // 将t点对各点的距离更新到dist取最小
            for(int i = 1; i <= n; ++ i) {
                dist[i] = Math.min(dist[i], dist[t] + w[t][i]);
            }
        }
    }
}

解题思路：堆优化 Dijkstra（邻接表）

add方法：

【小航的算法日记】图论_最短路_17

AC代码：

class Solution {
    int N = 105, M = 6005;
    // 邻接表
    int[] head = new int[N], edge = new int[M], nextEdge = new int[M], weight = new int[M];
    int[] dist = new int[N];
    boolean[] visited = new boolean[N];
    int n, k, idx = 0;
    int INF = 0x3f3f3f3f;
    // src:源点 desv：目标点  weight边权重
    // 由源点src出发经编号idx的边指向目标点desv
    void add(int src, int desV, int weight) {  
        // 1.新建一条编为idx，指向desv的边 
        this.edge[idx] = desV;
        // 2.头插法
        this.nextEdge[idx] = head[src];
        this.head[src] = idx;
        // 3.赋权值
        this.weight[idx] = weight;
        idx ++;
    }
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; k = _k;
        // 初始化链表头
        Arrays.fill(head, -1);
        // 存图
        for(int[] t : ts) {
            int u = t[0], v = t[1], c = t[2];
            add(u, v, c);
        }
        // 最短路
        dijkstra();
        int ans = -1;
        // 遍历答案
        for(int i = 1; i <= n; ++ i) {
            ans = Math.max(ans, dist[i]);
        }
        return ans > INF / 2 ? -1 : ans;
    }
    void dijkstra() {
        // 初始化：未访问，不可达
        Arrays.fill(visited, false);
        Arrays.fill(dist, INF);
        dist[k] = 0;
        // 使用【优先队列】存储
        // 以（点编号，到起点的距离）进行存储，优先弹出最短距离较小的点
        PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[1] - b[1]);
        q.add(new int[]{k , 0});
        while(!q.isEmpty()) {
            int[] poll = q.poll();
            int id = poll[0], step = poll[1];
            // 如果弹出的点已被标记
            if(visited[id]) continue;
            visited[id] = true;
            for(int i = head[id]; i != -1; i = nextEdge[i]) {
                int j = edge[i]; // 得到的边指向的点
                if(dist[j] > dist[id] + weight[i]) {
                    dist[j] = dist[id] + weight[i];
                    q.add(new int[]{j, dist[j]});
                }
            }
        }

    }
}

解题思路：Bellman Ford & 类

AC代码：

class Solution {
    class Edge {
        int a, b, c;
        Edge(int _a, int _b, int _c) {
            a = _a; b = _b; c = _c;
        }
    }
    int N = 105, M = 6005;
    int[] dist = new int[N];
    int INF = 0x3f3f3f3f;
    int n, m, k;
    List<Edge> es = new ArrayList<>();
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; k = _k; m = ts.length;
        // 存图
        for(int[] t : ts) {
            int u = t[0], v = t[1], w = t[2];
            es.add(new Edge(u, v, w));
        }
        // 最短路
        bf();
        // 遍历答案
        int ans = 0;
        for(int i = 1; i <= n; ++ i) {
            ans = Math.max(ans, dist[i]);
        }
        return ans > INF / 2 ? -1 : ans;
    }
    void bf() {
        // 初始化
        Arrays.fill(dist, INF); dist[k] = 0;
        for(int p = 1; p <= n; ++ p) {
            int[] prev = dist.clone();
            for(Edge e : es) {
                int a = e.a, b = e.b, c = e.c;
                dist[b] = Math.min(dist[b], prev[a] + c);
            }
        }
    }
}

解题思路：Bellman Ford & 邻接表

由于边的数量级大于点的数量级，因此能够继续使用【邻接表】的方式进行遍历

遍历所有边的复杂度的下界为 O(n)，上界可以确保不超过 O(m)

AC代码：

class Solution {
    int N = 110, M = 6010;
    // 邻接表
    int[] he = new int[N], e = new int[M], ne = new int[M], w = new int[M];
    // dist[x] = y 代表从「源点/起点」到 x 的最短距离为 y
    int[] dist = new int[N];
    int INF = 0x3f3f3f3f;
    int n, m, k, idx;
    void add(int a, int b, int c) {
        e[idx] = b;
        ne[idx] = he[a];
        he[a] = idx;
        w[idx] = c;
        idx++;
    }
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; k = _k;
        m = ts.length;
        // 初始化链表头
        Arrays.fill(he, -1);
        // 存图
        for (int[] t : ts) {
            int u = t[0], v = t[1], c = t[2];
            add(u, v, c);
        }
        // 最短路
        bf();
        // 遍历答案
        int ans = 0;
        for (int i = 1; i <= n; i++) {
            ans = Math.max(ans, dist[i]);
        }
        return ans > INF / 2 ? -1 : ans;
    }
    void bf() {
        // 起始先将所有的点标记为「距离为正无穷」
        Arrays.fill(dist, INF);
        // 只有起点最短距离为 0
        dist[k] = 0;
        // 迭代 n 次
        for (int p = 1; p <= n; p++) {
            int[] prev = dist.clone();
            // 每次都使用上一次迭代的结果，执行松弛操作
            for (int a = 1; a <= n; a++) {
                for (int i = he[a]; i != -1; i = ne[i]) {
                    int b = e[i];
                    dist[b] = Math.min(dist[b], prev[a] + w[i]);
                }
            }
        }
    }
}

解题思路：SPFA（邻接表）

AC代码：

class Solution {
    int N = 110, M = 6010;
    int INF = 0x3f3f3f3f;
    // 邻接表
    int[] head = new int[N], edge = new int[M], nextEdge = new int[M], weight = new int[M];    
    int[] dist = new int[N];
    boolean[] visited = new boolean[N];
    int n, k, idx;
    // 头插法
    void add(int a, int b, int c) {
        // 创建边
        edge[idx] = b;
        // b这条边指向a指向的
        nextEdge[idx] = head[a];
        // a指向b
        head[a] = idx;
        weight[idx] = c;
        idx ++;
    }
    public int networkDelayTime(int[][] ts, int _n, int _k) {
        n = _n; k = _k;
        // 初始化链表头
        Arrays.fill(head, -1);
        // 存图
        for(int[] t : ts) {
            int u = t[0], v = t[1], c = t[2];
            add(u, v, c);
        }
        // 最短路
        spfa();
        // 遍历答案
        int ans = 0;
        for(int i = 1; i <= n; ++ i) {
            ans = Math.max(ans, dist[i]);
        }
        return ans > INF / 2 ? -1 : ans;
    }
    void spfa() {
        // 初始化
        Arrays.fill(visited, false);
        Arrays.fill(dist, INF);
        dist[k] = 0;
        // 存储点编号
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(k);
        visited[k] = true;
        while(!queue.isEmpty()) {
            int poll = queue.poll();
            visited[poll] = false; // 并标记为未入队
            // 使用该点更新其他点
            for(int i = head[poll]; i != -1; i = nextEdge[i]) {
                int j = edge[i];
                // 松弛操作
                if(dist[j] > dist[poll] + weight[i]) {
                    dist[j] = dist[poll] + weight[i];
                    if(visited[j]) continue;
                    queue.offer(j);
                    visited[j] = true;
                }
            }
        }
    }
}

题：787. K 站中转内最便宜的航班

有 n 个城市通过一些航班连接。给你一个数组 flights ，其中 flights[i] = [fromi, toi, pricei] ，表示该航班都从城市 fromi 开始，以价格 pricei 抵达 toi。

现在给定所有的城市和航班，以及出发城市 src 和目的地 dst，你的任务是找到出一条最多经过 k 站中转的路线，使得从 src 到 dst 的价格最便宜，并返回该价格。如果不存在这样的路线，则输出 -1。

示例 1：

输入: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出: 200
解释: 
城市航班图如下

【小航的算法日记】图论_最短路_18

从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200，如图中红色所示。

示例 2：

输入: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出: 500
解释: 
城市航班图如下

【小航的算法日记】图论_最短路_19

从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500，如图中蓝色所示。

提示：

1 <= n <= 100
0 <= flights.length <= (n * (n - 1) / 2)
flights[i].length == 3
0 <= fromi, toi < n
fromi != toi
1 <= pricei <= 104
航班没有重复，且不存在自环
0 <= src, dst, k < n
src != dst

解：

这是一道有边数限制的最短路

告诉了起点和终点，所以返回的结果是dist[终点]

解题思路： Bellman Ford + 邻接矩阵

在遍历所有的“点对/边”进行松弛操作前，需要先对 dist 进行备份，否则会出现「本次松弛操作所使用到的边，也是在同一次迭代所更新的」，从而不满足边数限制的要求。

AC代码：

class Solution {
    int N = 105, INF = 0x3f3f3f3f;
    int[] dist = new int[N];
    int[][] g = new int[N][N];
    int n, k, s, t;
    public int findCheapestPrice(int _n, int[][] flights, int _src, int _dst, int _k) {
        // 最多不超过k个中转点等价于不超过k+1条边
        n = _n; k = _k + 1; s = _src; t = _dst;
        // 初始化图
        for(int i = 0; i < N; ++ i) {
            for(int j = 0; j < N; ++ j) {
                g[i][j] = i == j ? 0 : INF;
            }
        }
        for(int[] t : flights) {
            int a = t[0], b = t[1], w = t[2];
            g[a][b] = w;
        }
        int ans = bf();
        return ans > INF / 2 ? -1 : ans;
    }
    int bf() {
        // 初始化
        Arrays.fill(dist, INF);
        dist[s] = 0;
        for(int limit = 0; limit < k; ++ limit) { // 最多不超过k+1,控制边数
            int[] clone = dist.clone(); // 保证是在同一次迭代所更新的
            for(int i = 0; i < n; ++ i) {
                for(int j = 0; j < n; ++ j) {
                    dist[j] = Math.min(dist[j], clone[i] + g[i][j]); // 松弛操作
                }
            }
        }
        // 已经告诉目的地，一定是返回dist[t]
        return dist[t];
    }
}

解题思路：Bellman Ford + 类

AC代码：

class Solution {
    class Edge {
        int x, y, w;
        Edge(int _x, int _y, int _w) {
            x = _x; y = _y; w = _w;
        }
    }
    int N = 110, INF = 0x3f3f3f3f;
    int[] dist = new int[N];
    List<Edge> list = new ArrayList<>();
    int n, s, t, k, m;
    public int findCheapestPrice(int _n, int[][] flights, int _src, int _dst, int _k) {
        n = _n; s = _src; t = _dst; k = _k + 1;
        // 存图
        for(int[] f : flights) {
            list.add(new Edge(f[0], f[1], f[2]));
        }
        m = list.size();
        int ans = bf();
        return ans > INF / 2 ? -1 : ans;
    }
    int bf() {
        Arrays.fill(dist, INF);
        dist[s] = 0;
        for(int i = 0; i < k; ++ i) {
            int[] clone = dist.clone();
            for(Edge e : list) {
                int x = e.x, y = e.y, w = e.w;
                // 注意是：clone[x] + w
                dist[y] = Math.min(dist[y], clone[x] + w);
            }
        }
        return dist[t];
    }
}

解题思路：Bellman Ford

AC代码：

class Solution {
    int N = 110, INF = 0x3f3f3f3f;
    int[] dist = new int[N];
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) {
        Arrays.fill(dist, INF); dist[src] = 0;
        for(int i = 0; i < k + 1; ++ i) {
            int[] clone = dist.clone();
            for(int[] f : flights) {
                int x = f[0], y = f[1], w = f[2];
                dist[y] = Math.min(dist[y], clone[x] + w);
            }
        }
        return dist[dst] > INF / 2 ? -1 : dist[dst];
    }
}

搜索

题：841. 钥匙和房间

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。

当你进入一个房间，你可能会在里面找到一套不同的钥匙，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。

给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入所有房间返回 true，否则返回 false。

示例 1：

输入：rooms = [[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。

示例 2：

输入：rooms = [[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。

提示：

n == rooms.length
2 <= n <= 1000
0 <= rooms[i].length <= 1000
1 <= sum(rooms[i].length) <= 3000
0 <= rooms[i][j] < n
所有 rooms[i] 的值 互不相同

解：

解题思路：BFS

AC代码：

class Solution {
    // 判断图的连通性
    // BFS
    public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        int len = rooms.size();
        boolean[] visited = new boolean[len];
        Arrays.fill(visited, false);
        visited[0] = true; // 假设第一个已被访问
        Queue<Integer> queue = new LinkedList<>(); // 访问队列
        queue.offer(0); // 加入第一个节点
        while(!queue.isEmpty()) {
            Integer roomKey = queue.poll();
            visited[roomKey] = true;
            for(Integer key : rooms.get(roomKey)) {
                if(!visited[key]) {
                    queue.offer(key);
                }
            }
        }
        for(boolean isVisit : visited) if(!isVisit) return false;
        return true;
    }
}

解题思路：DFS

AC代码：

class Solution {
    // DFS
    public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        int len = rooms.size();
        boolean[] visited = new boolean[len];
        Arrays.fill(visited, false);
        visited[0] = true;
        dfs(0, rooms, visited);
        for(boolean key : visited) if(!key) return false;
        return true;
    }
    // 不需要上次的结果，无需返回值
    // 出口：该元素已被访问，无元素可访问
    void dfs(int key, List<List<Integer>> rooms, boolean[] visited) {
        // if(visited[key]) return;
        visited[key] = true;
        for(Integer key_next : rooms.get(key)) {
            if(visited[key_next]) continue;
            dfs(key_next, rooms, visited);
        }
    }
}

题：127. 单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的转换序列是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> … -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回从 beginWord 到 endWord 的最短转换序列中的单词数目。如果不存在这样的转换序列，返回 0 。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

提示：

1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

解：

解题思路：朴素BFS解法

AC代码：

class Solution {
    // 无向图求最短路
    // 1.寻找点与点之间的联系（如果两个单词只差一个字符说明有联系）
    // 2.求起点和终点的最短距离 => BFS
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 将List转化为Set，提高查询速度
        HashSet<String> wordSet = new HashSet<>(wordList);
        if(wordSet.size() == 0 || !wordSet.contains(endWord)) return 0;
        // 记录单词路径长度
        Map<String, Integer> map = new HashMap<>();
        map.put(beginWord, 1);
        // BFS
        Queue<String> queue = new LinkedList<>();
        queue.offer(beginWord);
        while(!queue.isEmpty()) {
            String nowWord = queue.poll(); // 取到当前的点
            int path = map.get(nowWord);
            // 遍历寻找下一个点，遍历该字符串替换字符，注意判断
            for(int i = 0; i < nowWord.length(); ++ i) {
                char[] chars = nowWord.toCharArray();
                for(char j = 'a'; j <= 'z'; ++ j) {
                    if(chars[i] == j) continue;
                    chars[i] = j;
                    String newWord = String.valueOf(chars);
                    // 先遇到终点最短
                    if(newWord.equals(endWord)) return path + 1;
                    // 在变换集中寻找可变的下一个点，且未被访问过   
                    if(wordSet.contains(newWord) && !map.containsKey(newWord)) {
                        map.put(newWord, path + 1);
                        queue.offer(newWord);
                    }
                }
            }
        } 
        return 0; // 没有找到
    }
}

解题思路：双向BFS

朴素的 BFS 可能会带来「搜索空间爆炸」的情况，而空间的瓶颈主要取决于搜索空间中的最大宽度，所以我们采用双向BFS解决这个问题：同时从两个方向开始搜索，一旦搜索到相同的值，意味着找到了一条联通起点和终点的最短路径。

AC代码：

class Solution {
    // 无向图求最短路
    // 1.寻找点与点之间的联系（如果两个单词只差一个字符说明有联系）
    // 2.求起点和终点的最短距离 => BFS
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 将List转化为Set，提高查询速度
        HashSet<String> wordSet = new HashSet<>(wordList);
        if(wordSet.size() == 0 || !wordSet.contains(endWord)) return 0;
        // 距离字典
        Map<String, Integer> m1 = new HashMap<>();
        Map<String, Integer> m2 = new HashMap<>();
        // BFS
        // 使用双端队列
        Deque<String> d1 = new ArrayDeque<>();
        Deque<String> d2 = new ArrayDeque<>();
        d1.add(beginWord); m1.put(beginWord, 1);
        d2.add(endWord); m2.put(endWord, 1);
        // 双向遍历
        int res = -1;
        while(!d1.isEmpty() && !d2.isEmpty()) {
            // 优先拓展队列内元素少的方向
            if(d1.size() <= d2.size()) {
                res = update(d1, m1, m2, wordSet);
            } else {
                res = update(d2, m2, m1, wordSet);
            }
            if(res != -1) return res; // 已找到答案！
        }
        return 0; // 没有找到
    }
    // 更新队列，返回值：res +flag
    public int update(Deque<String> deque, Map<String, Integer> cur, Map<String, Integer> other, HashSet<String> wordSet) {
        // 单层遍历
        int size = deque.size();
        while(size -- > 0) {
            String nowWord = deque.pollFirst();
            int path = cur.get(nowWord);
            // 遍历单词，逐个替换比较
            for(int i = 0; i < nowWord.length(); ++ i) {
                char[] chars = nowWord.toCharArray();
                for(char j = 'a'; j <= 'z'; ++ j) {
                    if(chars[i] == j) continue; // 替换词和原词一样，无需替换
                    chars[i] = j;
                    String newWord = String.valueOf(chars);
                    if(wordSet.contains(newWord)) { // 保证这个单词一定存在
                        // 如果在另一个map中出现
                        if(other.containsKey(newWord)) return path + other.get(newWord);
                        // 在变换集中寻找可变的下一个点，且未被访问
                        if(!cur.containsKey(newWord)) {
                            cur.put(newWord, path + 1);
                            deque.addLast(newWord);
                        }
                    }   
                }
            }
        }
        return -1; // 没找到
    }
}

最小生成树

题：778. 水位上升的泳池中游泳

在一个 n x n 的整数矩阵 grid 中，每一个方格的值 grid[i][j] 表示位置 (i, j) 的平台高度。

当开始下雨时，在时间为 t 时，水池中的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台，但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离，也就是默认在方格内部游动是不耗时的。当然，在你游泳的时候你必须待在坐标方格里面。

你从坐标方格的左上平台 (0，0) 出发。返回你到达坐标方格的右下平台 (n-1, n-1) 所需的最少时间。

示例 1:

【小航的算法日记】图论_搜索_20

输入: grid = [[0,2],[1,3]]
输出: 3
解释:
时间为0时，你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置

示例 2:

【小航的算法日记】图论_搜索_21

输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释: 最终的路线用加粗进行了标记。
我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的

提示:

n == grid.length
n == grid[i].length
1 <= n <= 50
0 <= grid[i][j] < n2
grid[i][j] 中每个值 均无重复

解：

解题思路：Kruskal & 并查集

AC代码：

class Solution {
    int[] parent; int n;
    void union(int a, int b) {
        // a = find(a); b = find(b);
        // if(a == b) return;
        // parent[a] = parent[b];
        parent[find(a)] = parent[find(b)];
    }
    int find(int x) {
        if(parent[x] != x) parent[x] = find(parent[x]);
        return parent[x];
    }
    int getIdx(int i, int j) {
        return i * n + j;
    }
    // 查询两点是否联通
    boolean query(int a, int b) { 
        return find(a) == find(b);
    }
    public int swimInWater(int[][] grid) {
        n = grid.length;
        // 1.初始化并查集
        parent = new int[n * n];
        for(int i = 0; i < n * n; ++ i) parent[i] = i;
        // 2.存边 [a, b, w] a->b 权重：时间w
        List<int[]> edges = new ArrayList<>();
        for(int i = 0; i < n; ++ i) {
            for(int j = 0; j < n; ++ j) {
                // 二维坐标转转一位
                int idx = getIdx(i, j);
                parent[idx] = idx; 
                // 方向：向右、右下
                if(i + 1 < n) {
                    int a = idx, b =getIdx(i + 1, j);
                    int w = Math.max(grid[i][j], grid[i + 1][j]);
                    edges.add(new int[]{a, b, w});
                }
                if(j + 1 < n) {
                    int a = idx, b = getIdx(i, j + 1);
                    int w = Math.max(grid[i][j], grid[i][j + 1]); // 取两者的最大值
                    edges.add(new int[]{a, b, w});
                }
                
            }
        }
        // 3.根据权值排序
        Collections.sort(edges, (a, b) -> a[2] - b[2]); 
        // 4.每添加一条边，判断始尾是否联通
        int start = getIdx(0, 0), end = getIdx(n - 1, n - 1);
        for(int[] edge : edges) {
            int a = edge[0], b = edge[1], w = edge[2];
            union(a, b); // 合并
            if(query(start, end)) {
                return w;
            }
        }
        return 0;
    }
}

解题思路：二分 + BFS

Tips:「二分」的本质是两段性，并非单调性。只要一段满足某个性质，另外一段不满足某个性质，就可以用「二分」。

题目给定了 grid[i][j] 的范围是 [0, n² - 1]，所以答案必然落在此范围。

假设最优解为 min（恰好能到达右下角的时间），那么小于 min 的时间无法到达右下角，大于 min 的时间能到达右下角。因此在以最优解 min 为分割点的数轴上具有两段性，可以通过「二分」来找到分割点 min。

接着分析，假设最优解为 min，我们在 [l, r] 范围内进行二分，当前二分到的时间为 mid 时：

能到达右下角：必然有 min⩽mid，让 r = mid【mid可能是答案】
不能到达右下角：必然有 min > mid，让 l = mid + 1【mid绝对不是答案】

AC代码：

class Solution {
    int n;
    public int swimInWater(int[][] grid) {
        n = grid.length;
        int l = 0, r = n * n;
        while(l < r) {
            int mid = l + r >> 1;
            if(check(grid, mid)) { // BFS
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return r;
    }
    int[][] dirs = new int[][] {{1, 0}, {-1, 0}, {0, 1}, {0, -1}}; // 四个方向
    boolean check(int[][] grid, int time) {
        boolean[][] visited = new boolean[n][n];
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[]{0, 0});
        visited[0][0] = true;
        while(!queue.isEmpty()) {
            int[] from = queue.poll();
            int x = from[0], y = from[1];
            if(x == n - 1 && y == n - 1) return true;
            // 对四个方向进行遍历
            for(int[] dir : dirs) {
                int newX = x + dir[0], newY = y + dir[1];
                int[] to = new int[] {newX, newY};
                // 判断是否在区域，是否访问过，是否可移动到那
                if(inArea(to) && !visited[newX][newY] && canMove(grid, from, to, time)) {
                    visited[newX][newY] = true;
                    queue.offer(to);
                }
            }
        }
        return false;
    }
    boolean inArea(int[] point) {
        int x = point[0], y = point[1];
        return x >= 0 && x < n && y >= 0 && y < n; 
    }
    boolean canMove(int[][] grid, int[] from, int[] to, int time) {
        return time >= Math.max(grid[from[0]][from[1]], grid[to[0]][to[1]]);
    }
}

题：1631. 最小体力消耗路径

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的体力值是路径上相邻格子之间高度差绝对值的最大值决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

【小航的算法日记】图论_图论_22

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

【小航的算法日记】图论_单源最短路_23

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

【小航的算法日记】图论_算法_24

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106

解：

解题思路：Kruskal & 并查集

很多同学都会误认为这道题考察DP，事实上，当题目运行往任意方向移动时，考察的往往不是DP，而是图论。
从本质上说：DP问题是一类特殊的图论问题。

所以，当一道题我们决定往「图论」方向思考时，我们重点应该放在「如何建图」上。

AC代码：

class Solution {
    int col, row;
    int[] p;
    void union(int a, int b) {
        p[find(a)] = p[find(b)];
    }
    boolean query(int a, int b) {
        return find(a) == find(b);
    }
    int find(int x) {
        if(p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
    int getIdx(int x, int y) {
        return x * col + y;
    }
    public int minimumEffortPath(int[][] heights) {
        row = heights.length; col = heights[0].length;
        // 1.初始化并查集
        p = new int[row * col];
        for(int i = 0; i < p.length; ++ i) p[i] = i;
        // 2.存图
        List<int[]> edges = new ArrayList<>();
        for(int i = 0; i < row; ++ i) {
            for(int j = 0; j < col; ++ j) {
                int idx = getIdx(i, j);
                // 拓展方向：向右、右下
                if(i + 1 < row) {
                    int a = idx, b = getIdx(i + 1, j);
                    int w = Math.abs(heights[i][j] - heights[i + 1][j]);
                    edges.add(new int[] {a, b, w});
                }
                if(j + 1 < col) {
                    int a = idx, b = getIdx(i, j + 1);
                    int w = Math.abs(heights[i][j] - heights[i][j + 1]);
                    edges.add(new int[] {a, b, w});
                }
            }
        }
        // 3.升序
        Collections.sort(edges, (a, b) -> a[2] - b[2]);
        // 4.遍历
        int start = getIdx(0, 0), end = getIdx(row - 1, col - 1);
        for(int[] edge : edges) {
            int a = edge[0], b = edge[1], w = edge[2];
            union(a, b);
            if(query(start, end)) {
                return w;
            }
        }
        return 0;
    }
}

迭代加深

题：863. 二叉树中所有距离为 K 的结点

给定一个二叉树（具有根结点 root），一个目标结点 target ，和一个整数值 k 。

返回到目标结点 target 距离为 k 的所有结点的值的列表。答案可以以任何顺序返回。

示例 1：

【小航的算法日记】图论_图论_25

输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
输出：[7,4,1]
解释：所求结点为与目标结点（值为 5）距离为 2 的结点，值分别为 7，4，以及 1

示例 2:

输入: root = [1], target = 1, k = 3
输出: []

提示:

节点数在 [1, 500] 范围内
0 <= Node.val <= 500
Node.val 中所有值 不同
目标结点 target 是树上的结点。
0 <= k <= 1000

解：

解题思路：

树是一类特殊的图，我们将树转化为图的形式，然后BFS/迭代加深
点和边的数量接近 => 稀疏图 => 邻接表

AC代码：

class Solution {
    // 树是一类特殊的图，我们将树转化为图的形式，然后BFS/迭代加深
    // 点和边的数量接近 => 稀疏图 => 邻接表
    int N = 510, M = N * 2;
    // 权重均为1
    int[] head = new int[N], edge = new int[M], nextEdge = new int[M];
    int idx;
    void add(int a, int b) {
        edge[idx] = b;
        nextEdge[idx] = head[a];
        head[a] = idx;
        idx ++;
    } 
    boolean[] visited = new boolean[N];
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        List<Integer> ans = new ArrayList<>();
        Arrays.fill(head, -1);
        // 存图
        dfs(root);
        // BFS遍历
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(target.val);
        visited[target.val] = true;
        while(!queue.isEmpty() && k >= 0) {
            int size = queue.size();
            while(size -- > 0) {
                int poll = queue.poll();
                if(k == 0) {
                    ans.add(poll);
                    continue;
                }
                for(int i = head[poll]; i != -1; i = nextEdge[i]) {
                    int j = edge[i];
                    if(!visited[j]) {
                        queue.offer(j);
                        visited[j] = true;
                    }
                }
            }
            k --;
        }
        return ans;
    }
    void dfs(TreeNode root) {
        if(root == null) return;
        if(root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if(root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }
}

解题思路：

迭代加深：只需要搜索第K层即可

AC代码：

class Solution {
    int N = 510, M = N * 2;
    int[] head = new int[N], edge = new int[M], nextEdge = new int[M];
    int idx;
    void add(int a, int b) {
        edge[idx] = b;
        nextEdge[idx] = head[a];
        head[a] = idx;
        idx ++;
    }
    boolean[] visited = new boolean[N];
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        List<Integer> ans = new ArrayList<>();
        Arrays.fill(head, -1);
        dfs(root);
        visited[target.val] = true;
        find(target.val, k, 0, ans);
        return ans;
    }
    void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }
    void find(int root, int max, int cur, List<Integer> ans) {
        if(cur == max) {
            ans.add(root);
            return;
        }
        for(int i = head[root]; i != -1; i = nextEdge[i]) {
            int j = edge[i];
            if(!visited[j]) {
                visited[j] = true;
                find(j, max, cur + 1, ans);
            }
        }
    }
}

上一篇：【小航的算法日记】哈希

下一篇：SpringBoot2 常用注解

提问和评论都可以，用心的回复会被更多人看到评论

发布评论

相关文章

官方博客	全部文章	热门标签	班级博客
了解我们	网站地图	意见反馈

鸿蒙开发者社区	51CTO学堂
51CTO	软考资讯