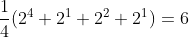背景:
一个正方形用红色和蓝色涂色给顶点涂色,方案有多少种呢?
如果不考虑对称,答案就该是2^4=16,考虑对称,结果就该是:

一共六种。Polya定理就是研究这样的分布问题。
定义一一映射关系
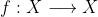
假设有:
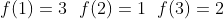
那么
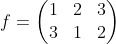
推广映射关系:
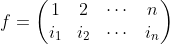
定义恒等排列:
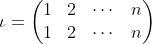
我们有:
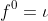
关于f的逆排列:设
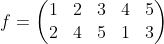
第一行和第二行互换:
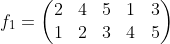
然后第一行以自然数的顺序排列:
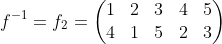
有:
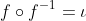
(

运算符表示二元映射操作)
以上也是寻找2行n列映射的逆的方法:1 .两行互换 2. 第一行自然数排列。
群:
定义集合 G={a,b,c……}和二元运算

,如果集合满足:
1. 封闭性。a -> G, b -> G, c=ab -> G
2. 结合律。
3. 有单位元。存在单位元e,使得G里的任意元素a满足
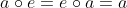
4. 逆元。G内的任意元素存在逆元,
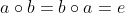
, 称b是a的逆元。
我们称G在

的运算下是一个群。
举例: G=(0,1,2,3,……7)在 mod 8的情况下是一个群。
ai与i变换——置换 :
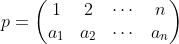
这是一个n阶置换,有排列数n!个
置换乘法也可以直接带入上诉过程,即
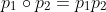
举例:
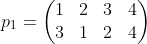
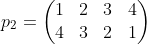
在置换乘法下,如果满足群的特质,成为置换群。
我们称
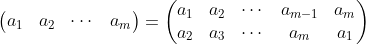
是一个循环置换。
对于下面的正方形:

顺时针旋转90度后,4个角对应的新点就是2 3 4 1,所以有
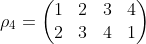
旋转2次,3次就分别对应:
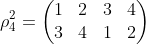
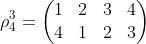
如果说两个循环没有共同文字,那么他们是不相交的。
不相交的循环相乘满足交换律。
任意置换可以表示成若干不相交循环的乘积,且表示是唯一的。例如:
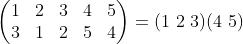
置换的循环节数是循环的个数。(上面的循环节是2)
Sn中的置换可以分解成格式:

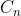
代表n阶循环的出现次数。
具有相同的格式的循环构成一个共轭类。属于共轭类的元素个数是
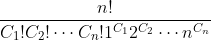
解释: 一个K阶循环可以重复K次(循环排列),如k=2, 有(1,2)(2,1)。那么
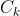
个K阶循环就有
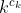
的重复
由于
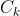
个K循环互不相交,所以有

次循环(全排列)
所以计算式就该是
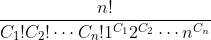
举例: 4个元素构成集合(1,2,3,4),
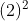
的共轭类有3个:
(1,2)(3,4)
(1,3)(2,4)
(1,4)(2,3)
计算:
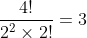
和结果一致。
K不动置换类:
设K是1--N的一个整数,G中使得K保持不变的置换全体,记做
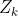
(G中使得K保持不变的置换类,简称K不动置换类)
举例:G={(1,2),(3,4),(1,2)(3,4)},那么有
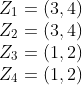
等价类:在群G的作用下,a变成b,b变成a,a和b属于同一类,K所属的等价类可以看成K在G的作用下的轨迹。
burnside引理:
设G是N={1,2,……,n} 上的置换群,G在N上可以引出不同的等价群,不同的等价群的个数是

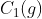
表示g中1阶循环的个数,|G|表示置换群的个数。
举例:回到最原始的问题,正方形四顶点涂色问题。如果我们不考虑旋转问题,那么它有这样的情况:

原始图像:
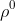
:
1 2 3 4 …… 15 16
1 2 3 4 …… 15 16
经过顺时针90旋转,各个图形看起来变了,如3 -> 6; 5 -> 4
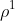
:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 2 6 3 4 5 10 7 8 9 12 11 16 13 14 15
再转90度:
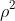
:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 2 5 6 3 4 9 10 7 8 11 12 15 16 13 14
旋转270度:
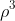
:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
1 2 4 5 6 3 8 9 10 7 12 11 14 15 16 13
计算:
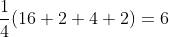
也即是这六种涂色方案:

ploya 定理:
设G={a_1,a_2,……,a_g} 是n个对象的置换群,用m种颜色给这n个对象着色,那么不同的着色方案数是
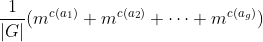
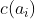
是置换
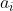
的循环节数
用polya定理来解决那个正方形涂色问题:
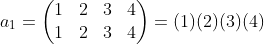
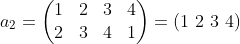
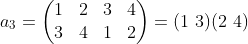
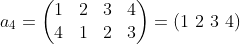
计算过程是