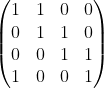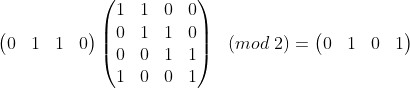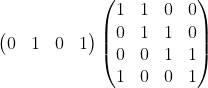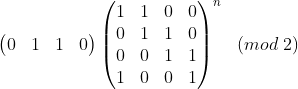hdu 2276 Kiki & Little Kiki 2（矩阵递推）

这题真心很棒，展现了矩阵递推的优雅。

​​http://acm.hdu.edu.cn/showproblem.php?pid=2276​​

大意：一串01数字，长度是n，第k位的数字的左边如果是1，他就会改变（0变1,1变0）。第1位数字的左边是第n位数字。问m次变换后串的样子。

分析: 由左右影响可以写出状态转移矩阵：

假设串的长度是4：

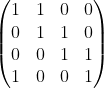
假设原串是0110，那么新串就是

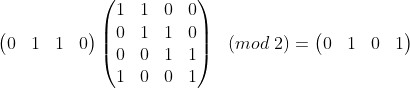
那么第二次后的串就该是在这个基础上右边再乘上状态转移矩阵：

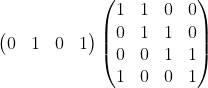
第N次后的串就是

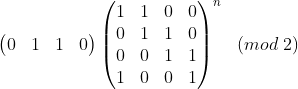
嗯，水到渠成。

（下面的取模不用位运算也行，直接使用%，多花时间16MS。当然，不能和其他大神的0ms相比。哈哈哈）

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n,m;
struct matrix{
    int m[105][105];
}I,A;
matrix multi(matrix a,matrix b){
    matrix c;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            c.m[i][j]=0;
            for(int k=0;k<n;k++){
                c.m[i][j]+=a.m[i][k]*b.m[k][j];
            }
            //c.m[i][j]%=2;
            c.m[i][j]&=1;
        }
    }
    return c;
}
matrix power(matrix a,int p){
    matrix ans=I;
    while(p){
        if(p&1)  ans=multi(ans,a);
        a=multi(a,a);
        p>>=1;
    }
    return ans;
}
int main()
{
    //freopen("cin.txt","r",stdin);
    char str[105];
    int s[105];
    int res[105];
    for(int i=0;i<105;i++) I.m[i][i]=1;
    while(cin>>m){
        scanf("%s",str);
        n=strlen(str);
        A=I;
        for(int i=0;i<n;i++){
            s[i]=str[i]-'0';
        }
        for(int i=0;i<n-1;i++){
            A.m[i][i+1]=1;
        }
        A.m[n-1][0]=1;
        matrix ans=power(A,m);
        memset(res,0,sizeof(res));
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                res[i]+=s[j]*ans.m[j][i];
            }
            //res[i]%=2;
            res[i]&=1;
            printf("%d",res[i]);
        }
        puts("");
    }
    return 0;
}