目录
1 概述
1.1 迭代法
1.2 Newton迭代法
2 不动点迭代
2.1 基本思想
2.2 案例及实现
3 牛顿迭代
3.1 基本思想
3.2 案例及实现
1 概述
在工程和科学技术中,许多问题常归结为求解函数方程:
f(x)=0
多项式函数,该方程为代数方程;如果f(x)为超越函数,该方程称为超越方程。如何求解方程f(x)=0的根是一个古老的数学问题。五次以上的代数方程和超越方程一般没有求根公式,很难或者无法求得其精确解,而实际应用中要得到满足一定精度的近似解就可以了。本解我们主要讲解不动点迭代和牛顿迭代的基本思想及代码。
1.1 迭代法

1.2 Newton迭代法

2 不动点迭代
2.1 基本思想
由f(x)=0==>x=φ(x)
若要求 x*满足 f(x*)=0,则 x*=φ(x*);反之亦然。则称 x*为函数 φ(x)的一个不动点。
选择一个初始近似值 x0,将它代入上式右端,即可求
x1=φ(x0)
可以如此反复迭代计算得到: xk+1=φ(xk),k=0,1,....(φ(x)称为迭代函数),更简单的说不动点也可看成y=φ(x)与y=x的交点。

不动点迭代收敛的过程:

对于左图,斜率小于零,迭代路径是一圈一圈的缩小;对于右图,斜率大于零,迭代路径是直接折线式逼近不动点。
不动点迭代发散的过程:

对于左图,斜率小于零,迭代路径是一圈一圈的变大;对于右图,斜率大于零,迭代路径是直接折线式远离不动点。
2.2 案例及实现

代码:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return (x+1)**(1/3)
def fun(x,tol,maxit):
x0=x
xk=x0
k=1
while (True):
xk=(x0+1)**(1/3)
if (xk-x0)*(xk-x0)<tol*tol:
print('Tolerance condition is satisfied:'+str(tol))
return xk
if k>maxit:
print('Maxiteration is satisfied:'+ste(maxit))
return xk
print("iter:"+str(k)+",xk="+str(xk))
x0=xk
k=k+1
def main():
x=1.5
maxit=20
tol=1.0*10**(-4)
result=fun(x,tol,maxit)
print(result)
x=np.arange(1,3,0.01)
y=x
x1=result
plt.plot(x,y,'b')
plt.scatter(x1,f(x1),color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
if __name__ =='__main__':
main()
结果:
iter:1,xk=1.3572088082974532
iter:2,xk=1.3308609588014277
iter:3,xk=1.325883774232348
iter:4,xk=1.324939363401885
iter:5,xk=1.3247600112927027
Tolerance condition is satisfied:0.0001
result= 1.3247259452268871

3 牛顿迭代
3.1 基本思想


牛顿-拉夫逊法提出来的思路就是利用切线是曲线的线性逼近这个思想。太佩服这两个大佬了,简直是顶礼膜拜,他们这脑袋瓜子怎么就那么聪明呢!上面我们的不动点迭代没有了导数和原函数的关系,但是我们这里的牛拉法不仅有原函数和导数的关系,还迭代速度特别快(不动点迭代是一阶的,牛-拉是二阶的),下面我们用图形来一起看看:


随便找一个曲线上的A点(为什么随便找,根据切线是切点附近的曲线的近似,应该在根点附近找,但是很显然我们现在还不知道根点在哪里),做一个切线,切线的根(就是和x轴的交点)与曲线的根,还有一定的距离。牛顿、-拉夫逊们想,没关系,我们从这个切线的根出发,做一根垂线,和曲线相交于B点,继续重复刚才的工作:
之前说过,B点比之前A点更接近曲线的根点,牛顿、拉弗森们很兴奋,继续重复刚才的工作:
第四次就已经很接近曲线的根了:


经过多次迭代后会越来越接近曲线的根(下图进行了50次迭代,哪怕经过无数次迭代也只会更接近曲线的根,用数学术语来说就是,迭代收敛了)

3.2 案例及实现
用牛顿迭代法求方程
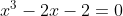
在[0,2]之间的根,要求:
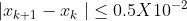
代码(方法1):
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def fun(x):
y = x ** 3 - 2 * x - 2
return y
def fun_diff(x):
y = 3 * x **(2) - 2
return y
def Netwon(x0, func, dfunc,eps):
x0=1.5
x = np.zeros(2)
x[0] = x0
x[1] = x0 - func(x[0]) / dfunc(x[0])
while np.abs(func(x[0])) > eps: # 在0附近
x[0] = x[1]
x[1] = x[0] - func(x[0]) / dfunc(x[0])
return x[1]
def main():
eps=10**(-3)
x = np.arange(-5, 5, 0.1)
y = fun(x)
x1 = Netwon(0, fun, fun_diff,eps) # 牛拉法求得的点
print("迭代值为:",x1)
plt.plot(x, y)
plt.xlim(-5, 5)
plt.ylim(-10, 50)
plt.scatter(x1, fun(x1), color='red')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
if __name__ == '__main__':
main()
结果:

代码(方法2):
import numpy as np
import matplotlib.pyplot as plt
def func(x):
return x**3-2*x-2
def gradfunc(x):
return 3*x**2-2
def Newton(f, gradf, x, tol, maxit):
x0 = x
xk = x0
k = 1
while (True):
gf = gradf(x0)
if gf * gf < 10 ** (-10):
print("gradient may zeros, please try it again by using another x")
return -1
xk = x0 - f(x0) / gf
if (xk - x0) * (xk - x0) < tol * tol:
print("Tolerance conditon is satisfied: " + str(tol))
return xk
if k > maxit:
print("Max iteration condition is satisfied: " + str(maxit))
return xk
print("iter:" + str(k) + "," + str(xk))
x0 = xk
k = k + 1
def main():
x = 1.5
maxit = 200
tol = 1.0 * 10 ** (-3)
result = Newton(func, gradfunc, x, tol, maxit)
print("迭代值 = " + str(result))
x=np.arange(-3,5,0.01)
y = func(x)
plt.xlim(-3, 5)
plt.ylim(-20, 60)
x1 = result
plt.plot(x, y, 'b')
plt.scatter(x1, func(x1), color='red')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
if __name__ == '__main__':
main()
结果:
iter:1,1.8421052631578947
iter:2,1.7728269199921578
iter:3,1.7693012925504517
Tolerance conditon is satisfied: 0.001
迭代值 = 1.7692923542960053