题目：不动点迭代（Fixed Point Iteration）

        本篇介绍不动点迭代（Fixed Point Iteration）。之所以学习不动点迭代是由于近来看到了FPC算法，即Fixed Point Continuation，有关FPC后面再详述。

        从搜索到的资料来看，不动点迭代是一个很基本很常见的概念，具体出自哪一门基础课不详，反正之前我没听说过。

        不动点迭代可以求解方程f(x)=0在区间[a,b]内的根。

1、不动点（FixedPoint）

        首先来看一下什么是不动点【1】：

python不动点迭代法程序 不动点迭代函数构造_斜率

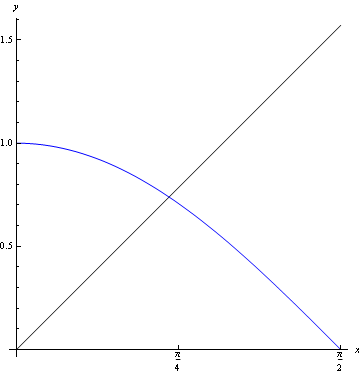
        换句话说，函数φ的不动点是y=φ(x)与y=x的交点，下图画出了函数y=cos(x)与y=x在区间[0,π/2]的交点，即cos(x)的不动点【2】：

python不动点迭代法程序 不动点迭代函数构造_python不动点迭代法程序_02

2、不动点迭代（Fixed Point Iteration）

        不动点迭代又称为简单迭代（simple iteration）。下面来看一下不动点迭代【3】：

python不动点迭代法程序 不动点迭代函数构造_斜率_03

也就是说，为了求解方程f(x)=0，首先将方程转换为x=g(x)，然后初始化x0，循环迭代xi+1=g(xi)，直到满足收敛收件。

        这里将方程f(x)=0转换为x=g(x)是很容易的，比如对于f(x)=x-cos(x)，求解f(x)=0即为求解x-cos(x)=0，即x=cos(x)，因此g(x)=cos(x)；再例如对于方程【4】

python不动点迭代法程序 不动点迭代函数构造_初始化_04

可以等价为

python不动点迭代法程序 不动点迭代函数构造_斜率_05

还可以等价为

python不动点迭代法程序 不动点迭代函数构造_python不动点迭代法程序_06

也就是说，将方程f(x)=0转换为x=g(x)有不同的方式，因此对方程f(x)=0来说，g(x)也不是唯一的。

3、不动点迭代的收敛性

        这个迭代过程是很简单的，但这里有个关键性的问题：迭代收敛么？即经过N次迭代后是否会收敛于不动点？

3.1 例子

        先看两个例子，这里有两个方程【5】：

python不动点迭代法程序 不动点迭代函数构造_python不动点迭代法程序_07

可以通过其它方法得到方程E1和E2的根：

python不动点迭代法程序 不动点迭代函数构造_斜率_08

画出E1和E2曲线：

python不动点迭代法程序 不动点迭代函数构造_python不动点迭代法程序_09

 

python不动点迭代法程序 不动点迭代函数构造_python不动点迭代法程序_10

3.2 不动点迭代MATLAB程序

        为了运用不动点迭代求E1和E2的根，我编写了如下MATLAB程序： 


function [y] = FixedPointIter(x0,func,tol,MaxIter)
% Version: 1.0 written by jbb0523 @2016-08-21
    if nargin < 4
        MaxIter = 100;
    end
	if nargin < 3
        tol = 1e-3;
    end
    xn = x0;
    fprintf('Iter  0: %16.14f\n',x0);
    xnp1 = func(xn);
    fprintf('Iter  1: %16.14f\n',xnp1);
    criterion = abs(xnp1-xn);
    xn = xnp1;
    Iter = 1;
    while(criterion>tol)
        xnp1 = func(xn);
        criterion = abs(xnp1-xn);
        xn = xnp1;
        Iter = Iter + 1;
        fprintf('Iter %2.0d: %16.14f\n',Iter,xnp1);
        if Iter>=MaxIter
            break;
        end
    end
    y = xnp1;
end

3.3 例子测试与分析

        分别在CommandWindow中执行以下两条命令：


FixedPointIter(0,@E1,1e-12,10);



FixedPointIter(3,@E2,1e-12,10);

        注意，以上两条命令分别调用了E1和E2函数：


function [y] = E1(x)
    y = 1+0.5*sin(x);
end



function [y] = E2(x)
    y = 3+2*sin(x);
end

可对E1和E2分别执行10次不动点迭代：

python不动点迭代法程序 不动点迭代函数构造_迭代_11

        从迭代过程来看，对E1执行不动点迭代后收敛了，而对E2执行不动点迭代后明显发散了。

        那么什么时候不动点迭代收敛，而又什么时候不动点迭代发散呢？

        注意起始点的设定，对于E1来讲，其根约为1.4987，迭代时初始化为0（这个初始点与根比较远），而最终收敛到了约1.4987，而对于E2来讲，其根约为3.0945，迭代时初始化为3（这个初始点与根很接近），但最终发散了。

        因此，这不能怪起始点不照顾E2……

        观察E1和E2曲线，我们大概可以得到一个直觉，E1在不动点处曲线较为平坦，而E2在不动点处曲线较为陡峭。

3.4 不动点迭代收敛定理

        下面给出有关不动点迭代收敛性的定理【4】：

python不动点迭代法程序 不动点迭代函数构造_初始化_12

通俗点讲，若要使不动点迭代收敛，则要求φ(x)在区间[a,b]上的函数值也在此区间内，另外还要求φ(x)的斜率绝对值不大于1。其证明过程比较复杂，有兴趣的可以查阅一些相关文献。

        应用此定理，可以来解释两个例子中为什么E1收敛而E2发散【5】：

python不动点迭代法程序 不动点迭代函数构造_斜率_13

python不动点迭代法程序 不动点迭代函数构造_迭代_14

        我们可以通过下图来直观的感觉一下不动点迭代收敛的过程【2】：

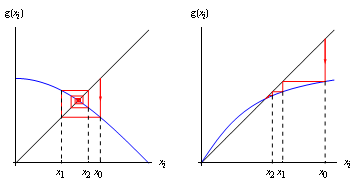
python不动点迭代法程序 不动点迭代函数构造_斜率_15

对于左图，斜率小于零，迭代路径是一圈一圈的缩小；对于右图，斜率大于零，迭代路径是直接折线式逼近不动点。

        我们再通过下图来直观的感觉一下不动点迭代发散的过程【2】：

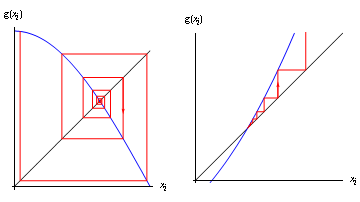
python不动点迭代法程序 不动点迭代函数构造_初始化_16

对于左图，斜率小于零，迭代路径是一圈一圈的变大；对于右图，斜率大于零，迭代路径是直接折线式远离不动点。

        注意看上图时与迭代过程相结合才能看明白，先给定x0，得到x1=φ(x0)，再得到x2=φ(x1)，依此类推……

4、结束语

        其实本来是在看SpaRSA（后面再说），里面有个Continuation，然后就查到了FPC，一直很好奇FPC为什么要Fixed Point Continuation，虽然FPC文献中一直提到Fixed Point Iteration和Fixed Point Equation，但也也没注意，后来看到了【6】，里面再一次提到了Fixed Point Iteration，难道Fixed Point Iteration是一个数学问题么？于是才开始百度……

        压缩感知凸优化类重构算法这个坑太大，每一个算法的背后都有一堆剪不断理还乱的数学问题……

        继续前行吧，还是那句话：路会越走越宽的……