LeetCode刷题day32

今日刷题重点–二叉树的递归+迭代遍历

​​144. 二叉树的前序遍历​​

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

其他相似问题

​​145. 二叉树的后序遍历​​

​​94. 二叉树的中序遍历​​

1.递归

//递归的做法
class Solution {
  public:
    void traverse(TreeNode* cur,vector<int>& vec) { //递归遍历
      if(cur) { //先序遍历
        vec.push_back(cur->val);
        traverse(cur->left,vec);
        traverse(cur->right,vec);
      }
    }
    vector<int> preorderTraversal(TreeNode* root) {
      vector<int> vec;
      traverse(root,vec);
      return vec;
    };

};

2.迭代

先序遍历

因为递归底层使用的是栈,所以我们可以直接使用栈来解决问题.
先序是按照中左右的顺序,每次先处理的是中间节点,那么我们处理时要先将右孩子加入栈,再加入左孩子.

为什么要按照这样的入栈顺序呢?因为先入栈的后遍历,后入栈的先遍历.

如图所示:

参考代码:

//先序遍历 中左右
    vector<int> preorderTraversal(TreeNode* root) {
      stack<TreeNode*> tab;
      vector<int> res;
      if(root==NULL) {
        return res;
      }
      tab.push(root);
      while(!tab.empty()) {
        TreeNode* cur = tab.top();
        tab.pop();
        res.push_back(cur->val);
        if(cur->right) {
          tab.push(cur->right);
        }
        if(cur->left) {
          tab.push(cur->left);
        }
      }
      return res;
    };

后序遍历

由于先序是:中左右,后序是:左右中,所以我们可以调整下先序代码的顺序便可完成操作.

//后序遍历: 左右中  可以直接从前序的代码上修改一点即可.
    vector<int> postorderTraversal(TreeNode* root) {
      stack<TreeNode*> tab;
      vector<int> res;
      if(root==NULL) {
        return res;
      }
      tab.push(root);
      while(!tab.empty()) {
        TreeNode* cur = tab.top();
        tab.pop();
        res.push_back(cur->val);
        if(cur->left) {
          tab.push(cur->left);
        }
        if(cur->right) {
          tab.push(cur->right);
        }

      }
      reverse(res.begin(),res.end());
      return res;
    }

中序遍历

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

//中序遍历
    vector<int> inorderTraversal(TreeNode* root) {
      vector<int> res;
      stack<TreeNode*> tab;
      TreeNode* cur = root;
      if(root==NULL){
        return res;
      }
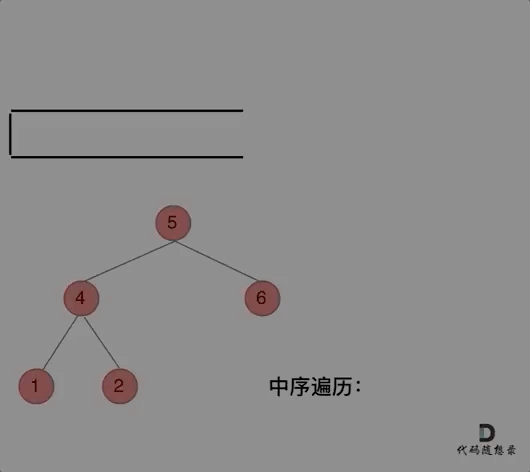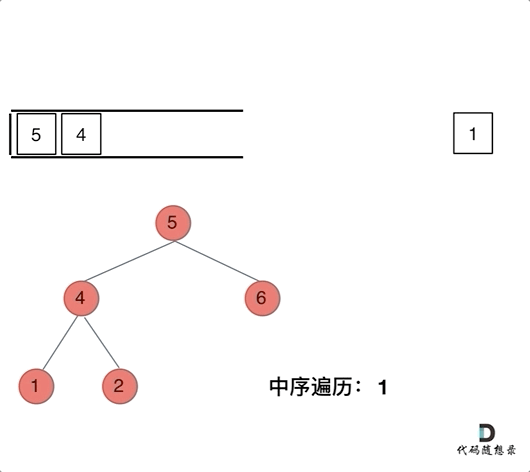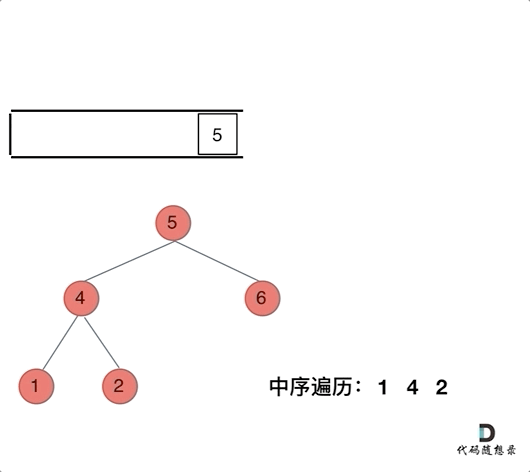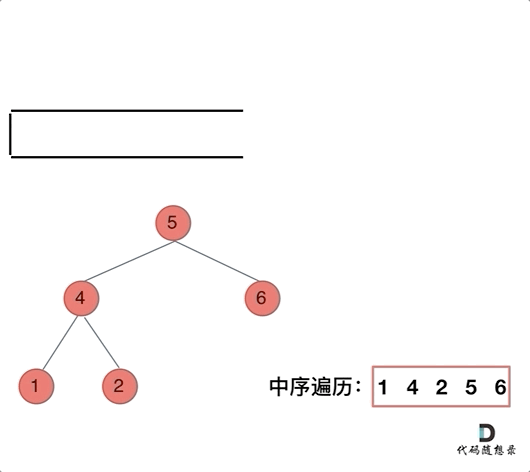
      while(cur!=NULL || !tab.empty()){//直到栈为空并且当前节点 也为空,则结束. 
        if(cur!=NULL){
          tab.push(cur);//如果当前节点不为空,则将当前节点先压入栈,继续进行访问. 
          cur = cur->left;//当把当前结点的左子树访问完了,在处理当期节点.  =>左 
        }else{//结点的左子树为空,则开始弹出该节点处理完毕后,开始访问处理右子树. 
          cur = tab.top();//
          tab.pop();
          res.push_back(cur->val);//中
          cur = cur->right; //右 
        } 
      } 
      return res; 
    }