【Codeforces 785D】范德蒙恒等式

1.​​题目链接​​。题目大意：一个由括号构成的序列，让你找到这个序列中有多少个好的子序列。一个好的子序列的定义是这样的：

                                         

2.分析：这个题是一个组合数学问题。对于每一个'(',我们统计它的左边有多少个和它相同的，右边有多少个和它相对的。也就是在这个左括号的左边选出i个左括号，右边选出i+1个右括号。（为什么是i+1,因为当前的括号是左括号，加上左边i个，所以右边需要有i+1个与之匹配）所以我们枚举这个i，就可以知道当前这个位置对答案的贡献。那么当前这个位置对答案的贡献就是：

                                           

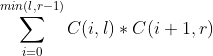
根据组合数的性质：C（n,i)=C(n,n-i).我们可以把后边的式子改写成:

                                                                        

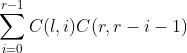
这个式子是可以用范德蒙恒等式化简的：

                                                    范德蒙恒等式：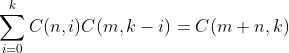

这个式子的证明很简单，考虑一个多项式：

                                                          

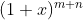
其中x的k次幂：就是右边的式子，如果我们把 这个多项式拆解成：

                                                      

那么对于右边的式子：我们再考录x的k次方，即可得到范德蒙恒等式。

那么对于我们的上边的式子可以做出一下化简：

                        

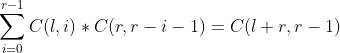
这样对于每一个点，我们在预处理之后，就可以O(1)的计算这个点对答案的贡献。代码如下：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 200010;
const int mod = 1e9 + 7;
char s[maxn];
int l[maxn], r[maxn];
#pragma warning(disable:4996)
ll qpow(ll a, ll b, ll mod)
{
  ll res = 1;
  while (b)
  {
    if (b & 1)
      res = res * a%mod;
    a = a * a%mod;
    b >>= 1;
  }
  return res;
}
ll fac[maxn] = { 1,1 }, inv[maxn] = { 1,1 }, f[maxn] = { 1,1 };
ll c(ll a, ll b)
{
  return fac[b] * inv[a] % mod*inv[b - a] % mod;
}
void init() 
{
  for (int i = 2; i < maxn; i++) 
  {
    fac[i] = fac[i - 1] * i%mod;
    f[i] = (mod - mod / i)*f[mod%i] % mod;
    inv[i] = inv[i - 1] * f[i] % mod;
  }
}
int main()
{
  scanf("%s", s);
  int len = strlen(s);
  l[0] = (s[0] == '(');
  r[len - 1] = (s[len - 1] == ')');
  for (int i = 1; i < len; i++)
    l[i] = l[i - 1] + (s[i] == '(');
  for (int i = len - 2; i >= 0; i--)
    r[i] = r[i + 1] + (s[i] == ')');
  init();
  ll ans = 0;
  for (int i = 0; i < len; i++)
  {
    if (s[i] == '(')
    {
      ans = (ans + c(r[i] - 1, l[i] + r[i] - 1));
      ans %= mod;
    }
  }
  printf("%lld\n", ans);
}