【BZOJ 2142 】礼物

1.​​题目链接​​。首先物品总量大于等于需求就可满足条件，否则才是Impossible。然后就是简单的推理了，高中组合数问题： 首先给第一个人分配，C(n,w1),第二个人：C(n-w1,w2)....第i个人：C(n-sum(wi),wi+1).根据分步乘法，答案就是这些数乘起来。

                                                                            

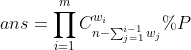
但是这里需要对p取模，我们知道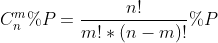：              .显然涉及了除法，在分母与P不互质时，是无法求逆元的。这里就是一个经典的问题了，首先，我们把P做唯一分解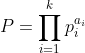： .然后分别求 每一个: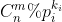.用CRT合并这个解。那么这里还是没有解决分母与模数不互质，因为就是分解成素因子的乘积，也不能保证他们互质：那么现在问题转化为如何求解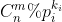：。求解它是一个很famous的算法，Exlucas算法。也就是拓展lucas算法，其实这个和lucas定理已经没有关系了，一般是习惯性这么叫。它的核心思想有点类似于组合数取模时做质因子分解取模一样。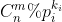求解这个组合数，我们可以看出来，之所以不互质是因为组合数里面可能含有pi这个素因子，那么我们可以把它像提取公因子一样提取出来，然后剩下的部分就是互质的，这样就可以求逆元，求完之后再乘上我们提取出来的公因子。完美的解决了不互质。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int SIZE = 300;
ll A, B, Mod, m[SIZE], r[SIZE];
inline void input(void)
{
  scanf("%lld%lld%lld", &A, &B, &Mod);
  //计算C(A,B)%Mod
}
inline ll power(ll a, ll b, ll p)
{
  ll res = 1;
  while (b)
  {
    if (1 & b)res = res * a % p;
    b >>= 1;
    a = a * a % p;
  }
  return res;
}
inline ll Exeuclid(ll a, ll& x, ll b, ll& y, ll c)
{
  if (!b) { x = c / a, y = 0; return a; }
  else
  {
    ll p = Exeuclid(b, x, a % b, y, c);
    ll x_ = x, y_ = y;
    x = y_, y = x_ - a / b * y_;
    return p;
  }
}
inline ll inv(ll a, ll p)
{
  ll x_, y_;
  Exeuclid(a, x_, p, y_, 1);
  return (x_ + p) % p;
}
//计算x!中除去val后模p意义下的值,val是一个素数。
inline ll calc(ll x, ll val, ll p)
{
  if (!x)return 1;
  ll res = 1, last = x % p;
  for (ll i = 1; i <= p; i++)
    if (i % val)res = res * i % p;
  res = power(res, x / p, p);
  for (ll i = 1; i <= last; i++)
    if (i % val)res = res * i % p;
  return res * calc(x / val, val, p) % p;
}
//计算 C(A,B,prime,prime^k)
inline ll C(ll d, ll u, ll val, ll Pow)
{
  if (u > d)return 0;
  ll mulup = calc(d, val, Pow), k = 0;
  ll muldown1 = calc(u, val, Pow), muldown2 = calc(d - u, val, Pow);
  //计算该
  for (ll i = d; i; i /= val)k += i / val;
  for (ll i = u; i; i /= val)k -= i / val;
  for (ll i = d - u; i; i /= val)k -= i / val;
  //计算剩余的val的指数
  return mulup * inv(muldown1, Pow) % Pow * inv(muldown2, Pow) % Pow * power(val, k, Pow) % Pow;
}
inline ll CRT(int cnt)
{
  ll m_ = Mod, M[SIZE] = {}, t[SIZE] = {}, res = 0;
  for (int i = 1; i <= cnt; i++)
    M[i] = m_ / m[i];
  for (int i = 1; i <= cnt; i++)
  {
    ll y;
    Exeuclid(M[i], t[i], m[i], y, 1);
    res = (res + r[i] % m_ * M[i] % m_ * t[i] % m_) % m_;
  }
  return (res % m_ + m_) % m_;
}
inline ll Exlucas(void)
{
  memset(m, 0, sizeof(m));
  memset(r, 0, sizeof(r));
  int temp = Mod, cnt = 0;
  for (ll i = 2; i * i <= Mod; i++)
  {
    if (temp % i == 0)
    {
      m[++cnt] = 1;
      while (temp % i == 0)
        temp /= i, m[cnt] *= i;
      r[cnt] = C(A, B, i, m[cnt]);
    }
  }
  if (temp > 1) m[++cnt] = temp, r[cnt] = C(A, B, temp, m[cnt]);
  return CRT(cnt);
}
int W[110];
int main()
{
  scanf("%d", &Mod);
  int n, m;
  scanf("%d%d", &n, &m);
  ll sum = 0;
  for (int i = 1; i <= m; i++)
  {
    scanf("%d", &W[i]);
    sum += W[i];
  }
  ll ans =1;
  A = n;
  if (sum > n)
  {
    puts("Impossible");
    return 0;
  }
  for (int i = 1; i <= m; i++)
  {
    B = W[i];
    ans = (ans*Exlucas()) % Mod;
    A -= W[i];
  }
  printf("%lld\n", ans % Mod);

  return 0;
}