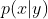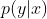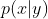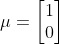## **转载声明**

这位博主的文章相当好，点赞！

​

—————————————————————–

同朴素贝叶斯一样，高斯判别分析（Gaussian discriminant analysismodel, GDA）也是一种生成学习算法，在该模型中，我们假设y给定的情况下，x服从混合正态分布。通过训练确定参数，新样本通过已建立的模型计算出隶属不同类的概率，选取概率最大为样本所属的类。

一、混合正态分布（multivariate normal distribution）

混合正态分布也称混合高斯分布。该分布的期望和协方差为多元的：期望​​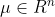

【转载】斯坦福大学机器学习——高斯判别分析_协方差

​​,协方差​​

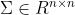
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_02

​​，协方差具有对称性和正定性。混合高斯分布：​​

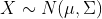
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_03

​​，它的的概率密度函数为：

​​

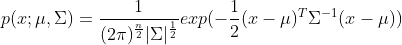
【转载】斯坦福大学机器学习——高斯判别分析_协方差_04

​​

其中，​​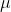

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_05

​​为混合高斯分布的期望​​

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_06

​​，​​

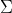
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_07

​​为其协方差​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_08

​​，​​

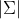
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_09

​​表示协方差的行列式。​​

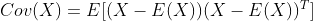
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_10

​​

下面用图形直观的看一下二维高斯分布的性质：

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_11

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_12

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_13

以上三个图形的期望都为：​​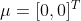

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_14

​​，最左端图形的协方差​​

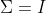
【转载】斯坦福大学机器学习——高斯判别分析_协方差_15

​​，中间的​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_16

​​，最右端的​​

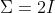
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_17

​​，我们可以看出：当​​

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_18

​​变小时，图像变得更加“瘦长”，而当​​

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_19

​​增大时，图像变得更加“扁平”。

再看看更多的例子：

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_20

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_21

【转载】斯坦福大学机器学习——高斯判别分析_协方差_22

以上三个图形的期望都为：​​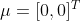

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_23

​​，从左至右三个图形的协方差分别的：

​​

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_24

​​​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_25

​​​​

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_26

​​

可以看到随着矩阵的逆对角线数值增加，图形延​​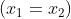

【转载】斯坦福大学机器学习——高斯判别分析_协方差_27

​​方向，即底部坐标45度角压缩。图形在这个方向更加“扁”。

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_28

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_29

【转载】斯坦福大学机器学习——高斯判别分析_协方差_30

以上三幅图分别是以上图形的等高线，可以更直观的看到调整逆对角线的数值对图像的压缩程度。

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_31

 

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_32

 

【转载】斯坦福大学机器学习——高斯判别分析_协方差_33

以上三幅图保持协方差不变，期望的值分别为

​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_34

​​；​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_35

​​；​​

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_36

​​

可以看出，随着期望的改变，图形在平面上平移，而其他特性保持不变。

二、高斯判别分析模型

如果特征值x是连续的随机变量，我们可以使用高斯判别分析模型完成特征值的分类。为了简化模型，假设特征值为二分类，分类结果服从0-1分布。（如果为多分类，分类结果就服从二项分布）

模型基于这样的假设：

​​

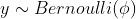
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_37

​​

​​

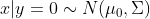
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_38

​​

​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_39

​​

他们的概率（密度）函数分别为：

​​

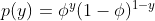
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_40

​​

​​

【转载】斯坦福大学机器学习——高斯判别分析_协方差_41

​​

​​

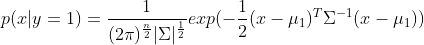
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_42

​​

模型的待估计参数为

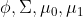
【转载】斯坦福大学机器学习——高斯判别分析_协方差_43

，通常模型有两个不同的期望，而有一个相同的协方差。

该模型的极大似然对数方程为：

                                                                                         ​​

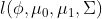
【转载】斯坦福大学机器学习——高斯判别分析_协方差_44

​​

                                                        ​​

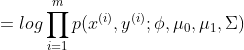
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_45

​​

                                                        ​​

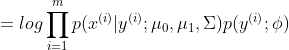
【转载】斯坦福大学机器学习——高斯判别分析_协方差_46

​​

求解该极大似然方程得：

​​

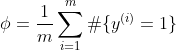
【转载】斯坦福大学机器学习——高斯判别分析_正态分布_47

​​

​​

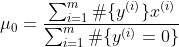
【转载】斯坦福大学机器学习——高斯判别分析_协方差_48

​​

​​

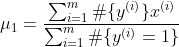
【转载】斯坦福大学机器学习——高斯判别分析_协方差_49

​​

​​

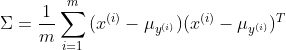
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_50

​​

在对

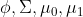
【转载】斯坦福大学机器学习——高斯判别分析_协方差_51

计算完成之后，将新的样本x带入进建立好的模型中，计算出​​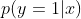

【转载】斯坦福大学机器学习——高斯判别分析_正态分布_52

​​、​​

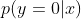
【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_53

​​，选取概率更大的结果为正确的分类。

三、GDA和logistic回归

GDA模型和logistic回归模型存在这样有趣的关系：假如我们将​​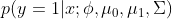

【转载】斯坦福大学机器学习——高斯判别分析_协方差_54

​​视作关于x的函数，该函数可以表示成logistic回归形式：


​​

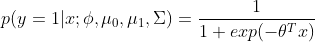
【转载】斯坦福大学机器学习——高斯判别分析_协方差_55

​​

其中，​​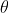

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_56

​​可以用以

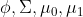
【转载】斯坦福大学机器学习——高斯判别分析_协方差_57

为变量的函数表示。

前文中已经提到，如果​​

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_58

​​为混合高斯分布，那么，​​

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_59

​​就可以表示成logistic回归函数形式；相反，如果可表示成logistic回归函数形式，并不代表​​

【转载】斯坦福大学机器学习——高斯判别分析_logistic回归_60

​​服从混合高斯分布。这意味着GDA比logistic回归需要更加严格的模型假设，当然，如果混合高斯模型的假设是正确的，那么，GDA具有更高的拟合度。基于以上原因，在实践中使用logistic回归比使用GDA更普遍。