
一.定义
队列是一种先进先出的数据结构,就好比是排队进站,位置靠前就先进站
二.存储结构
(一)顺序结构
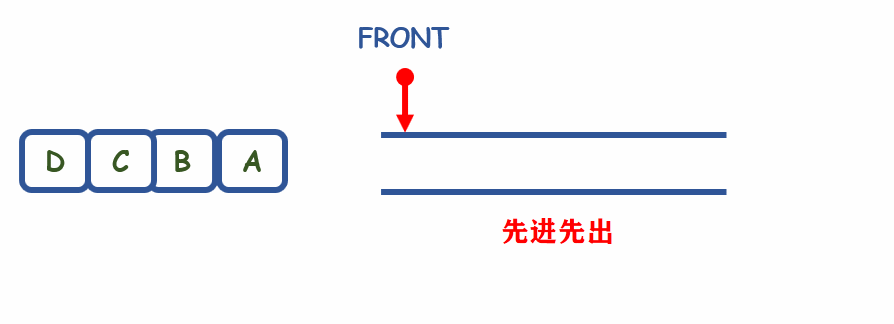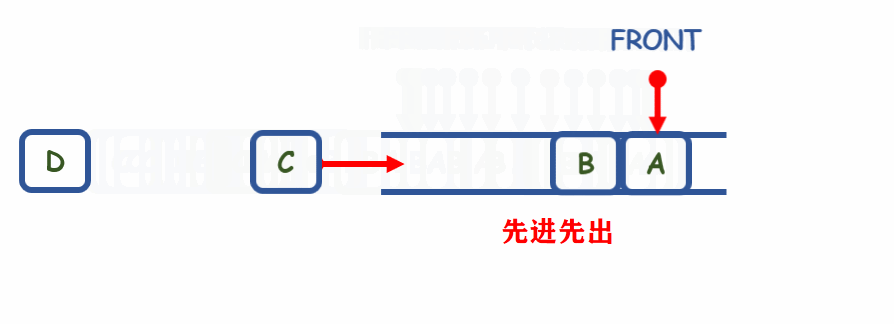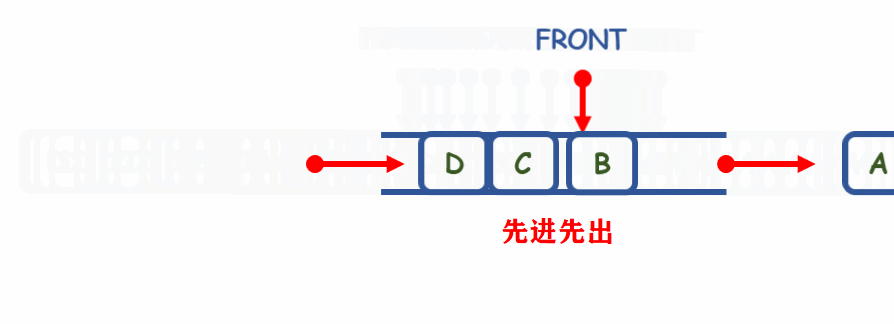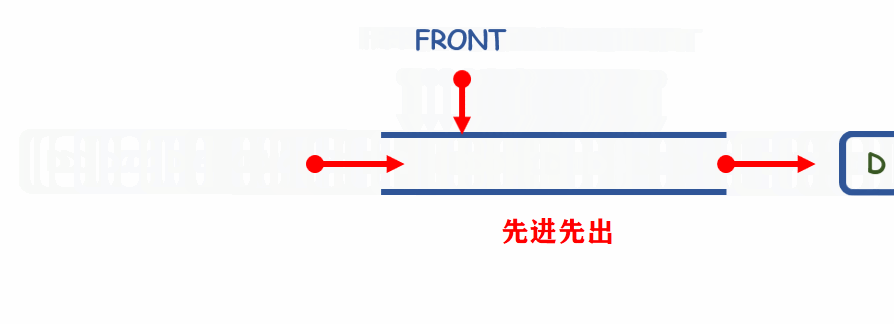
解释:顺序队列由于空间有限,会有可能产生溢出的情况,但是对于链队可以很好解决这个问题
(二)链式结构
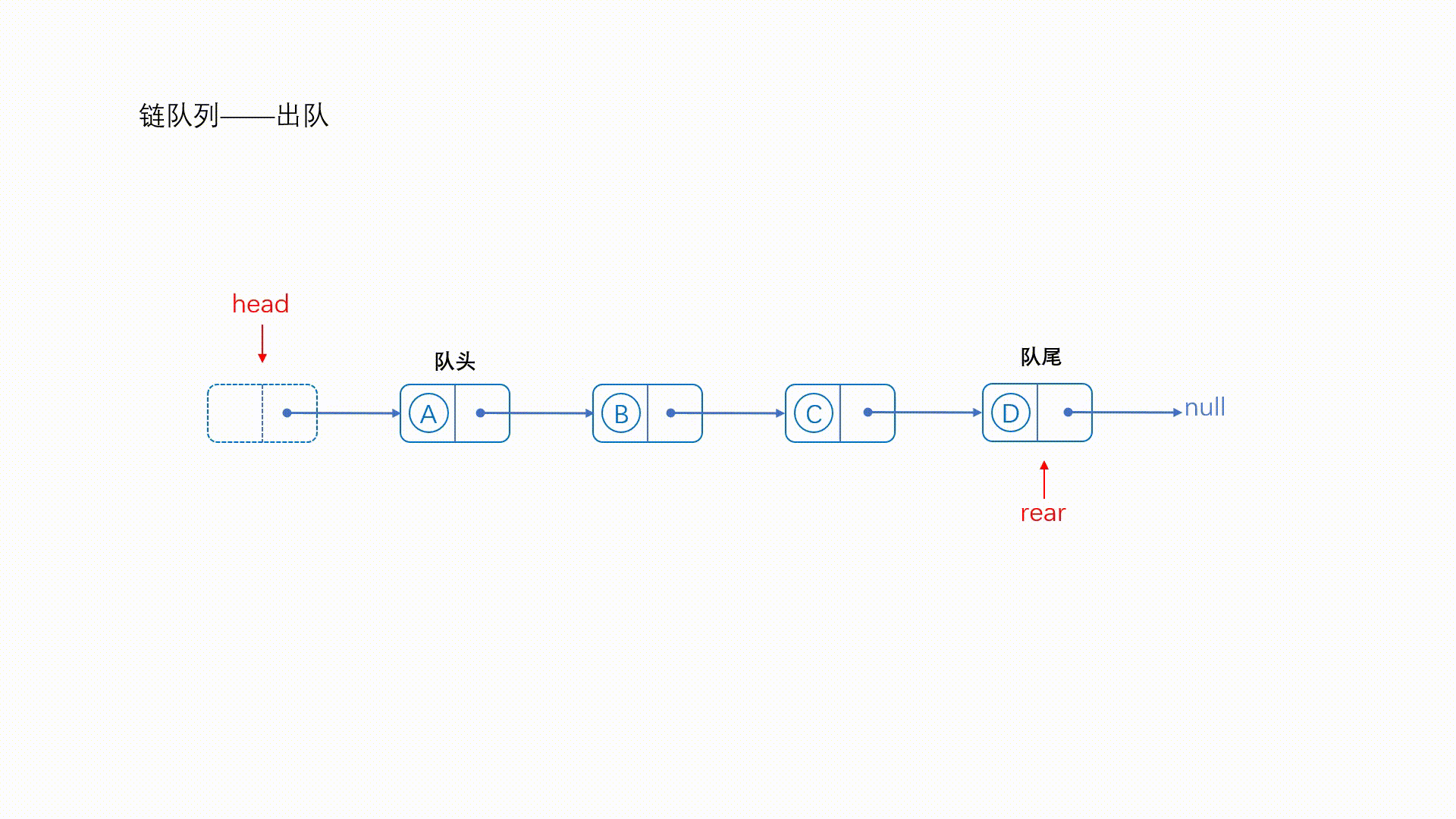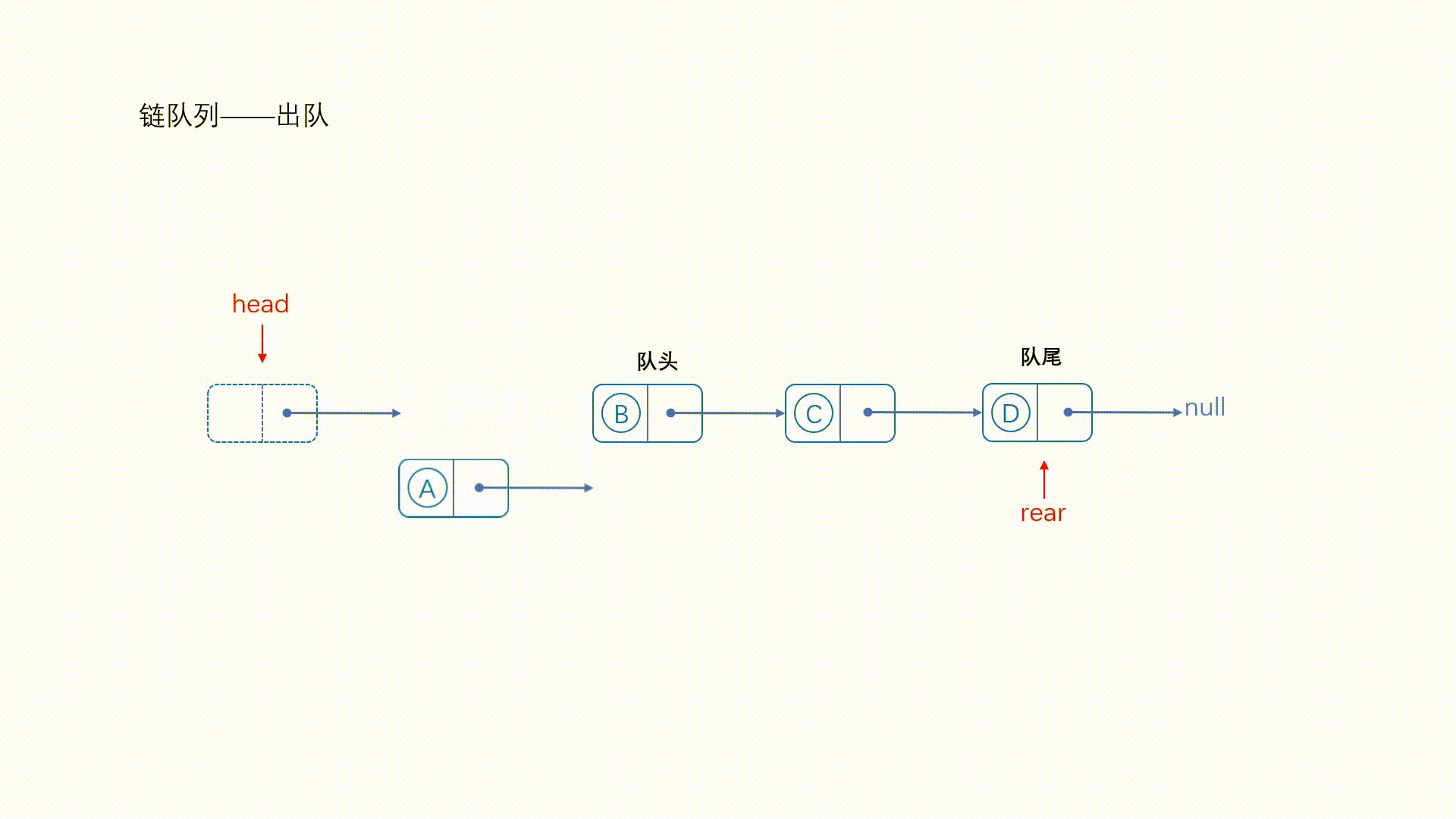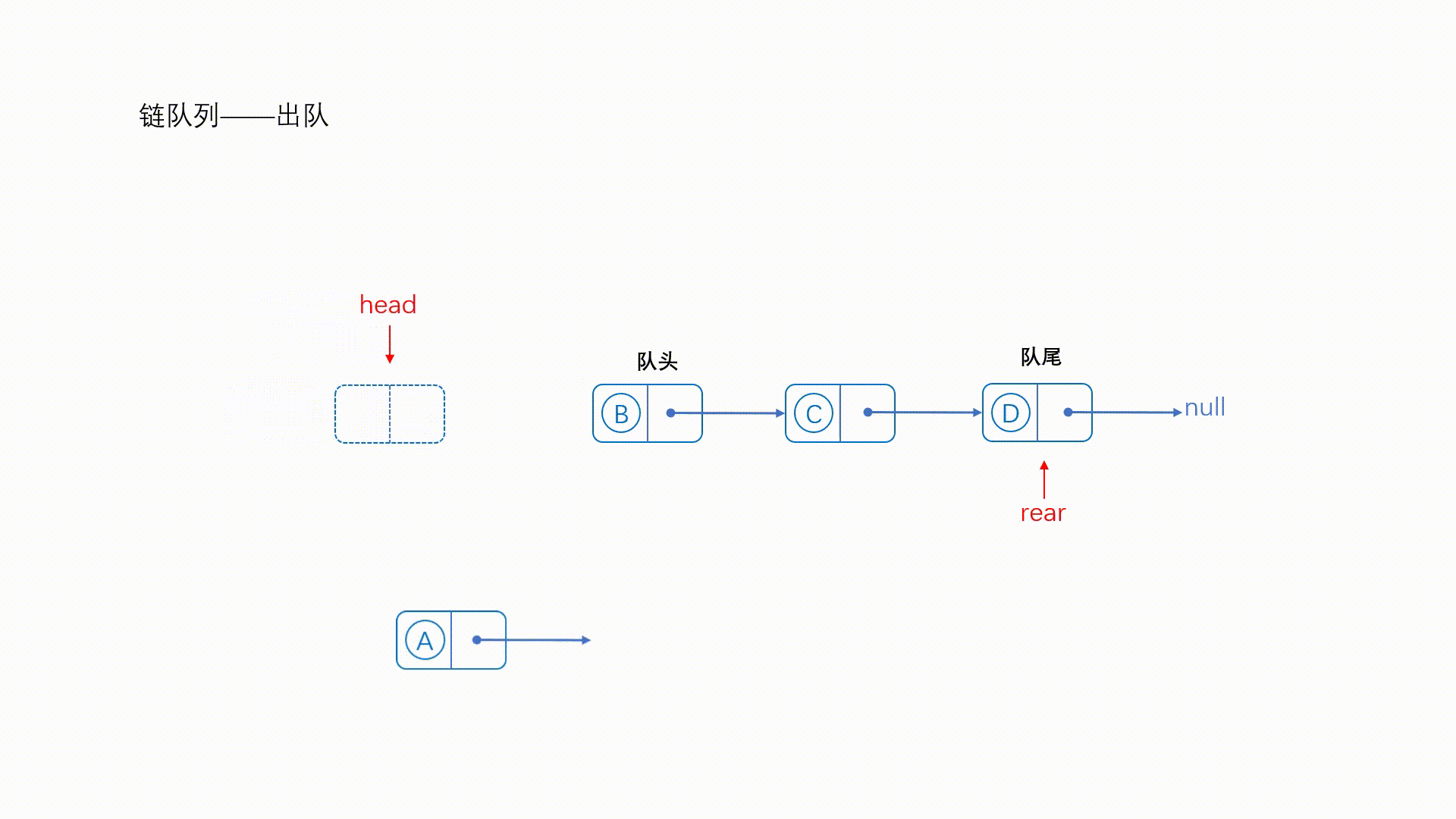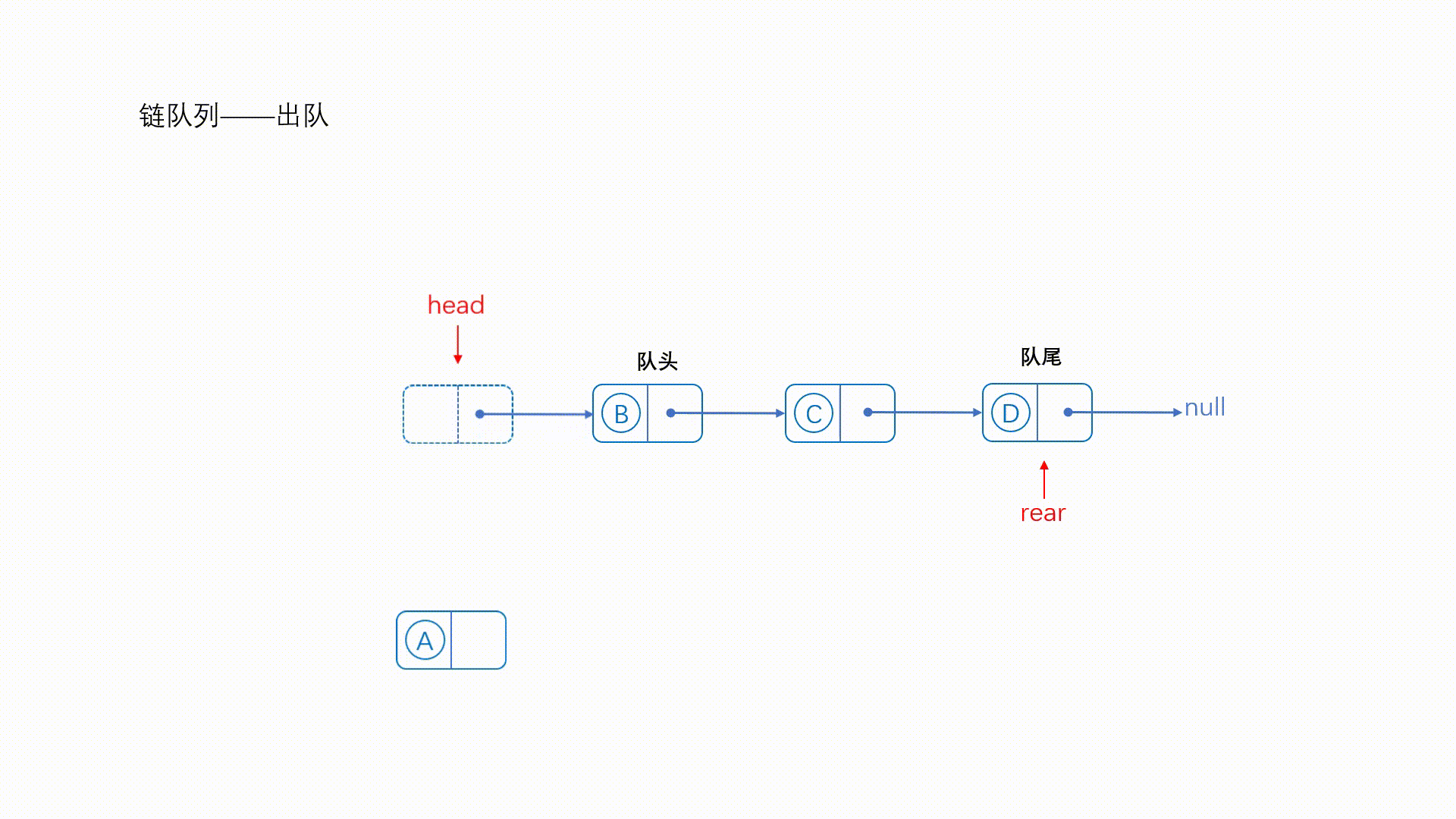
解释:链队可以根据需要添加结点,节约空间,并且不会产生溢出的情况
三.基本操作代码
(一)顺序队列
/*循环队列顺序存储基本操作*/
//队列所能达到的最大长度
typedef struct{
int *base; //存储空间的基地址
int front; //头指针
int rear; //尾指针
}SqQueue;
//函数声明
void InitQueue(SqQueue *Q); //队列初始化
int QueueLength(SqQueue *Q); //求队列长度
void Enqueue(SqQueue *Q,int e);//入队
void DeQueue(SqQueue *Q,int e);//出队
int GetHead(SqQueue *Q); //取循环队列头元素
//主函数
int main(){
int i,total,key,length;
SqQueue *Q;
InitQueue(Q);
printf("请输入入队元素总数:\n");
scanf("%d",&total);
printf("请输入元素:\n");
for(i=0;i<total;i++){
scanf("%d",&key);
Enqueue(Q,key);
}
if(i==total){
printf("入队成功!\n");
}
DeQueue(Q,key);
length=QueueLength(Q);
printf("队列的长度为:%d\n",length);
key=GetHead(Q);
printf("队头元素为%d\n",key);
return 0;
}
//初始化
void InitQueue(SqQueue *Q) //构造一个空队列Q
{
Q->base=new int[MAXQSIZE];//为队列分配一个最大容量为MAXQSIZE的数组空间
if(!Q->base)
printf("空间分配失败!\n");
else{
Q->front=Q->rear=0;
printf("队列初始化成功!\n");
}
}
//求队列长度
int QueueLength(SqQueue *Q) //返回Q的元素个数,即队列的长度
{
return (Q->rear-Q->front+MAXQSIZE)%MAXQSIZE;
}
//入队
void Enqueue(SqQueue *Q,int e) //插入e为Q的新的队尾元素
{
if((Q->rear+1)%MAXQSIZE==Q->front)
printf("队列已满!\n");
else{
Q->base[Q->rear]=e;
Q->rear=(Q->rear+1)%MAXQSIZE;
}
}
//出队
void DeQueue(SqQueue *Q,int e)//删除Q的队头元素,用e返回其值
{
if(Q->front==Q->rear)
printf("队列已空!\n");
else{
e=Q->base[Q->front]; //保存队头元素
Q->front=(Q->front+1)%MAXQSIZE; //队头指针加1
printf("元素%d出队成功!\n",e);
}
}
//取循环队列的头元素
int GetHead(SqQueue *Q)//返回Q的队头元素,不修改头指针
{
if(Q->rear==Q->front)
printf("队列已空!\n");
else{
return Q->base[Q->front];//返回队头元素的值,队头指针不变
}
}
(二)链队
/* 队列的链式存储结构 基本操作:初始化、入队、出队、取队头元素 */
//结点
typedef struct QNode{
int data; //数据域
struct QNode *next;//指针域
}QNode,*QueuePtr;
typedef struct {
QueuePtr front;//队头指针
QueuePtr rear;//队尾指针
}LinkQueue;
//函数声明
void InitQueue(LinkQueue *Q); //队列的初始化
void EnQueue(LinkQueue *Q,int key); //入队
void DeQueue(LinkQueue *Q,int key); //出队
void GetHead(LinkQueue *Q); //取队头元素
//主函数
int main(){
LinkQueue *Q;
int total,i,key;
InitQueue(Q);
printf("请输入进队元素总数:\n");
scanf("%d\n",&total);
for (i=0;i<total;i++){
scanf("%d",&key);
EnQueue(Q,key);
}
if(i==total){
printf("入队成功!\n");
}
while(Q)
{
DeQueue(Q,key);
}
return 0;
}
//初始化
void InitQueue(LinkQueue *Q)//构造一个空队列Q
{
Q->front=Q->rear=new QNode;//生成新结点作为头结点,队头和队尾指针指向此结点
Q->front->next=NULL; //头结点的指针
printf("初始化成功!\n");
}
//入队
void EnQueue(LinkQueue *Q,int key)//插入元素key为Q的新的队尾元素
{
QNode *p=new QNode; //为入队元素分配结点空间,用指针p指向
p->data = key; //将新结点的数据域置为key
p->next=NULL; //将新结点插入到队尾
Q->rear->next=p;
Q->rear=p; //修改队尾指针
}
//出队
void DeQueue(LinkQueue *Q,int key)//删除Q的队头元素,用key返回其值
{
QNode *p;
if(Q->front==Q->rear)
printf("队列已空!\n");
p=Q->front->next; //p指向队头元素
key = p->data; //e用来保存队头元素的值
Q->front->next=p->next; //修改头结点的指针域
if(Q->rear==p) Q->rear=Q->front; //最后一个元素被删,队尾指针指向头结点
delete p; //释放原队头元素空间
printf("出队元素为%d\n",key);
}
//取队头元素
void GetHead(LinkQueue *Q) //返回Q的队头元素,不修改队头指针
{
if(Q->front!=Q->rear)
printf("队列已空!\n");
else{
printf("队头元素为%d",Q->front->next->data);//Q->front初始指向头指针
}
}
约瑟夫环
/* 15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,
于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海
如此循环进行直到仅余15个人为止。求活着的人的序号。
*/
/*
有n个人围城一圈,按顺序编号,从第一个人开始报数,从1报到m,凡报到m的人退出圈子,
然后接着报数,问最后留下来那几位是多少?
*/
//数组
//用长度为n的数组存储人的编号,退出的人编号置为0,当15个人都退出后,剩下的那个编号不为0的人就是要找的人。
void left_num(int* a,int n,int m) {
int out = 0,count = 0,i =0; //out为出去的人数,count为报数,i为目前报到第几个人
int *p = a;
int num = 0;
for(num = 0;num < n;num++)
{
*(a+num) = num+1;
} //为n个人编号1-n
while (out != 15)
{
if (*(p+i) != 0)
{
count ++; //不等于0才报数+!
}
if (count%m==0 && *(p+i)!=0)
{
//printf("出队的序号为:%d",*(p+i));
*(p+i) = 0;
count=0;
out++; //报道m那么,出列人数out+1,且内容置0,报数置0
printf("%d\n",i+1);
}
i++;
if (i == n)
{
i = 0;//到队尾重头开始
}
}
//输出剩下的人
for (num = 0; num < n; num++) {
if (*(a+num) != 0)
{
printf("left num:%d\n",*(a+num));
}
}
}
int main()
{
int m,n;
int a[50] = {0};
printf("Please input total num:");
scanf("%d",&n);
printf("Please input out num:");
scanf("%d",&m);
printf("leave sequence:\n");
left_num(a,n,m);
return 0;
}























