机器学习是一门理论性和实战性都比较强的技术学科。在应聘机器学习相关工作岗位时,我们常常会遇到各种各样的机器学习问题和知识点。为了帮助大家对这些知识点进行梳理和理解,以便能够更好地应对机器学习笔试包括面试。红色石头准备在公众号连载一些机器学习笔试题系列文章,希望能够对大家有所帮助!
Q1. 关于“回归(Regression)”和“相关(Correlation)”,下列说法正确的是?注意:x 是自变量,y 是因变量。
A. 回归和相关在 x 和 y 之间都是互为对称的
B. 回归和相关在 x 和 y 之间都是非对称的
C. 回归在 x 和 y 之间是非对称的,相关在 x 和 y 之间是互为对称的
D. 回归在 x 和 y 之间是对称的,相关在 x 和 y 之间是非对称的
答案:C
解析:相关(Correlation)是计算两个变量的线性相关程度,是对称的。也就是说,x 与 y 的相关系数和 y 与 x 的相关系数是一样的,没有差别。
回归(Regression)一般是利用 特征 x 预测输出 y,是单向的、非对称的。
Q2. 仅仅知道变量的均值(Mean)和中值(Median),能计算的到变量的偏斜度(Skewness)吗?
A. 可以
B. 不可以
答案:B
解析:偏斜度是对统计数据分布偏斜方向及程度的度量。偏斜度是利用 3 阶矩定义的,其计算公式如下:
S c =∑(x i −x ¯ ) 3 m Sc=∑(xi−x¯)3m
其中,n 是样本数量。统计数据的频数分布有的是对称的,有的是不对称的,即呈现偏态。在偏态分布中,当偏斜度为正值时,分布正偏,即众数位于算术平均数的左侧;当偏斜度为负值时,分布负偏,即众数位于算术平均数的右侧。
我们可以利用众数、中位数和算术平均数之间的关系判断分布是左偏态还是右偏态,但要度量分布偏斜的程度,就需要计算偏斜度了。
Q3. 假设有 n 组数据集,每组数据集中,x 的平均值都是 9,x 的方差都是 11,y 的平均值都是 7.50,x 与 y 的相关系数都是 0.816,拟合的线性回归方程都是 y = 3.00 + 0.500*x。那么这 n 组数据集是否一样?
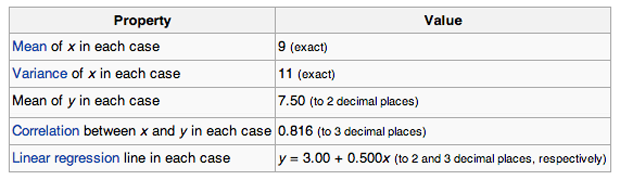 A. 一样 B. 不一样 C. 无法确定 **答案**:C **解析**:这里需要知道的是 Anscombe’s quartet。1973年,统计学家F.J. Anscombe 构造出了四组奇特的数据。这四组数据中,x 值的平均数都是 9.0,y 值的平均数都是 7.5;x 值的方差都是 10.0,y值的方差都是 3.75;它们的相关度都是 0.816,线性回归线都是 y=3+0.5x。单从这些统计数字上看来,四组数据所反映出的实际情况非常相近,而事实上,这四组数据有着天壤之别,如下图所示:
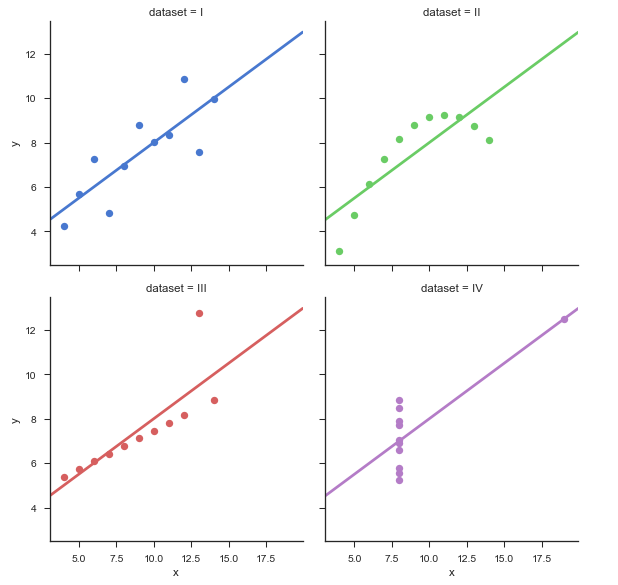 相应的 Python 代码为:
import seaborn as sns
sns.set(style="ticks")
# Load the example dataset for Anscombe's quartet
df = sns.load_dataset("anscombe")
# Show the results of a linear regression within each dataset
sns.lmplot(x="x", y="y", col="dataset", hue="dataset", data=df,
col_wrap=2, ci=None, palette="muted", size=4,
scatter_kws={"s": 50, "alpha": 1})
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
Q4. 观察样本次数如何影响过拟合(多选)?注意:所有情况的参数都保持一致。
A. 观察次数少,容易发生过拟合
B. 观察次数少,不容易发生过拟合
C. 观察次数多,容易发生过拟合
D. 观察次数多,不容易发生过拟合
答案:AD
解析:如果样本观察次数较少,且样本数量较少,通过提高模型复杂度,例如多项式阶数,很容易对所有样本点都拟合的非常好,造成过拟合。但是,如果观察次数多,样本更具有代表性,这时候,即使模型复杂,也不容易发生过拟合,得到的模型能够较真实地反映真实的数据分布。
Q5. 假如使用一个较复杂的回归模型来拟合样本数据,使用 Ridge 回归,调试正则化参数 λ,来降低模型复杂度。若 λ 较大时,关于偏差(bias)和方差(variance),下列说法正确的是?
A. 若 λ 较大时,偏差减小,方差减小
B. 若 λ 较大时,偏差减小,方差增大
C. 若 λ 较大时,偏差增大,方差减小
D. 若 λ 较大时,偏差增大,方差增大
答案:C
解析:若 λ 较大时,意味着模型复杂度较低,这时候容易发生欠拟合,对应偏差增大,方差减小。做个简单总结:
-
λ 较小:偏差减小,方差增大,容易发生过拟合
-
λ 较大:偏差增大,方差减小,容易发生欠拟合
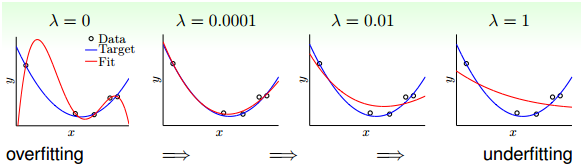 **Q6. 假如使用一个较复杂的回归模型来拟合样本数据,使用 Ridge 回归,调试正则化参数 λ,来降低模型复杂度。若 λ 较小时,关于偏差(bias)和方差(variance),下列说法正确的是?** A. 若 λ 较小时,偏差减小,方差减小 B. 若 λ 较小时,偏差减小,方差增大 C. 若 λ 较小时,偏差增大,方差减小 D. 若 λ 较小时,偏差增大,方差增大 **答案**:B **解析**:见 Q5。 **Q7. 下列关于 Ridge 回归,说法正确的是(多选)?** A. 若 λ=0,则等价于一般的线性回归 B. 若 λ=0,则不等价于一般的线性回归 C. 若 λ=+∞,则得到的权重系数很小,接近于零 D. 若 λ=+∞,则得到的权重系数很大,接近与无穷大 **答案**:AC **解析**:若 λ=0,即没有正则化项,等价于一般的线性回归,可以使用最小二乘法求解系数。若 λ=+∞,正则化项对权重系数的“惩罚”非常大,对应得到的权重系数很小,接近于零。 关于正则化的图形化解释,请参考我的这篇文章: [机器学习中 L1 和 L2 正则化的直观解释](https://blog.csdn.net/red_stone1/article/details/80755144) **Q8. 在下面给出的三个残差图中,下面哪一个代表了与其他模型相比更差的模型?** **注意:** **1. 所有的残差都已经标准化** **2. 图中横坐标是预测值,纵坐标是残差**
 A. 1 B. 2 C. 3 D. 无法比较 **答案**:C **解析**:预测值与残差之间不应该存在任何函数关系,若存在函数关系,表明模型拟合的效果并不很好。对应在图中,若横坐标是预测值,纵坐标是残差,残差应表现为与预测值无关的随机分布。但是,图 3 中残差与预测值呈二次函数关系,表明该模型并不理想。 **Q9. 下列哪一种方法的系数没有封闭形式(closed-form)的解?** A. Ridge 回归 B. Lasso C. Ridge 回归和 Lasso D. 以上都不是 **答案**:B **解析**:Ridge 回归是一般的线性回归再加上 L2 正则项,它具有封闭形式的解,可以基于最小二乘法求解。
J=12m ∑ i=1 m (y−y ^ ) 2 +λ2m ||w|| 2 J=12m∑i=1m(y−y^)2+λ2m||w||2
w=(X T X+λI) −1 X T y w=(XTX+λI)−1XTy
Lasso 回归是一般的线性回归再加上 L1 正则项,L1 正则项使解是非线性的,没有封闭形式的解。
J=12m ∑ i=1 m (y−y ^ ) 2 +λm |w| J=12m∑i=1m(y−y^)2+λm|w|
Q10. 观察如下数据集:
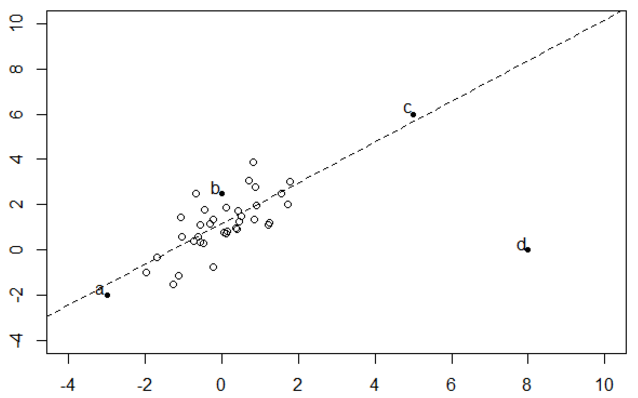 **删除 a,b,c,d 哪个点对拟合回归线的影响最大?** A. a B. b C. c D. d **答案**:D **解析**:线性回归对数据中的离群点比较敏感。虽然 c 点也是离群点,但它接近与回归线,残差较小。因此,d 点对拟合回归线的影响最大。 **Q11. 在一个简单的线性回归模型中(只有一个变量),如果将输入变量改变一个单位(增加或减少),那么输出将改变多少?** A. 一个单位 B. 不变 C. 截距 D. 回归模型的尺度因子 **答案**:D **解析**:很简单,假设线性回归模型是:y=a+bx,若 x 改变一个单位,例如 x+1,则 y 改变 b 个单位。b 是回归模型的尺度因子。 **Q12. 逻辑回归将输出概率限定在 [0,1] 之间。下列哪个函数起到这样的作用?** A. Sigmoid 函数 B. tanh 函数 C. ReLU 函数 D. Leaky ReLU 函数 **答案**:A **解析**:Sigmoid 函数的表达式和图形如下所示:
θ(s)=11+e −s θ(s)=11+e−s
! 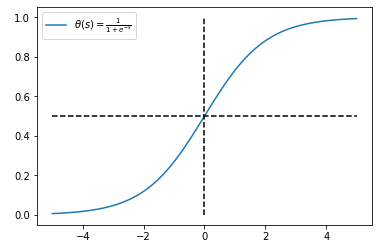 Sigmoid 函数输出值限定在 [0,1] 之间。 tanh 函数:
a=e z −e −z e z +e −z a=ez−e−zez+e−z
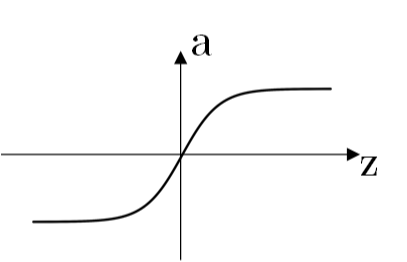 ReLU 函数:
a=max(0,z) a=max(0,z)
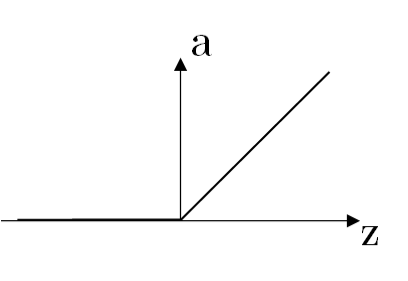 Leaky ReLU 函数:
a={λz,z, z≤0z>0 a={λz,z≤0z,z>0
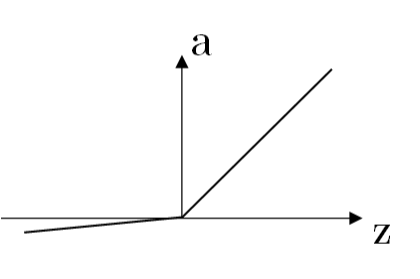 其中,λ 为可变参数,例如 λ=0.01。 **Q13. 线性回归和逻辑回归中,关于损失函数对权重系数的偏导数,下列说法正确的是?** A. 两者不一样 B. 两者一样 C. 无法确定 **答案**:B **解析**:线性回归的损失函数为:
J=12m ∑ i=1 m (y−y ^ ) 2 J=12m∑i=1m(y−y^)2
逻辑回归的损失函数为:
J=−12m ∑ i=1 m ylogy ^ +(1−y)log(1−y ^ ) J=−12m∑i=1mylogy^+(1−y)log(1−y^)
逻辑回归输出层包含了 Sigmoid 非线性函数,其损失函数对 Sigmoid 函数之前的线性输出 Z 的偏导数与线性回归的损失函数对线性输出 Z 的偏导数一样,都是:
dZ=Y ^ −Y dZ=Y^−Y
具体推导过程比较简单,此处省略。
dZ 是一样的,反向求导过程中,对所有权重系数的偏导数表达式都是一样的。
Q14. 假设使用逻辑回归进行 n 多类别分类,使用 One-vs-rest 分类法。下列说法正确的是?
A. 对于 n 类别,需要训练 n 个模型
B. 对于 n 类别,需要训练 n-1 个模型
C. 对于 n 类别,只需要训练 1 个模型
D. 以上说法都不对
答案:A
解析:One-vs-rest 分类法中,假设有 n 个类别,那么就会建立 n 个二项分类器,每个分类器针对其中一个类别和剩余类别进行分类。进行预测时,利用这 n个二项分类器进行分类,得到数据属于当前类的概率,选择其中概率最大的一个类别作为最终的预测结果。
举个简单的例子,3 分类,类别分别是 {-1, 0, 1}。构建 3 个 二分类器:
-
-1 与 0,1
-
0 与 -1,1
-
1 与 -1,0
若第 1 个二分类器得到 -1 的概率是 0.7,第 2 个二分类器得到 0 的概率是 0.2,第 3 个二分类器得到 1 的 概率是 0.4,则最终预测的类别是 -1。
Q15. 下图是两个不同 β0、β1 对应的逻辑回归模型(绿色和黑色):

关于两个逻辑回归模型中的 β0、β1 值,下列说法正确的是?
注意:y= β0+β1*x, β0 是截距,β1 是权重系数。
A. 绿色模型的 β1 比黑色模型的 β1 大
B. 绿色模型的 β1 比黑色模型的 β1 小
C. 两个模型的 β1 相同
D. 以上说法都不对
答案:B
解析:逻辑回归模型最终还要经过 Sigmoid 非线性函数,Sigmoid 是增函数,其图形与上图中的黑色模型相近。黑色模型是增函数,说明其 β1>0,绿色模型是减函数,说明其 β1<0。所以,得出结论:绿色模型的 β1 比黑色模型的 β1 小。




















