若尔当（约当/约旦）标准型的求解方法：
方法一：初等变换法
例：求矩阵 
STEP1：求 
注：定理指出，矩阵的特征矩阵（
）一定可以通过初等变换化为上述标准型，称为
矩阵的标准型。初等因子：
矩阵的标准型对角线上次数大于0且首项为1的一次方幂。本例题中，初等因子为
，
。
注：虽然上述两个初等因子对应的特征值相同，但是代表两个不同的若尔当块。
STEP2：写出每个初等因子对应的若尔当块
初等因子对应的特征值为对应若尔当块对角线元素，初等因子的阶数为对应若尔当块的阶数。
对应的若尔当块为：
；
对应的若尔当块为：
STEP3：写出若尔当标准型
与
的顺序可以变，但一般按照初等因子的顺序。
方法二：求特征值法
例：求矩阵
STEP1：求矩阵的特征值
令
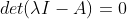
，解得
；
STEP2：求每个特征值的几何重数（相同特征值求一次即可）
几何重数：代表该特征值对应的若尔当块的个数；几何重数=特征矩阵的列数-rank(特征矩阵)。
本题中：
对应的几何重数=
=3-1=2。
STEP3：求每个特征值对应的若尔当块的最大阶数
设每个特征值对应的若尔当块的最大阶数为
，则
为使
成立的最小正整数。
引用
本题中，由于
为零矩阵，所以k=2，即
对应的若尔当块的最大阶数为2，所以
有两个若尔当块，一个一阶的，一个二阶的，即：
STEP4：写出若尔当标准型
与
的顺序可以变。
方法三：求Q矩阵（特征值均互异可用）
STEP1：求矩阵的特征值
STEP2：求矩阵的特征值对应的特征向量p1,p2,p3
STEP3：由特征向量组成Q矩阵
STEP4：求J
J=Q-1*A*Q
本文章为转载内容，我们尊重原作者对文章享有的著作权。如有内容错误或侵权问题，欢迎原作者联系我们进行内容更正或删除文章。
