解密树的平衡：二分搜索树 → AVL自平衡树 → 左倾红黑树

解密树的平衡：二分搜索树 → AVL自平衡树 → 左倾红黑树

• 二叉树框架
• 二分搜索树

• 验证
• 查找
• 添加
• 删除

• AVL平衡树

• 插入
• 删除

• 左倾红黑树

• 2-3 树
• 红黑树和 2-3 树的等价性
• 基本性质
• 插入
• 删除
• 白板编程红黑树

从二叉树框架开始，过渡到二分搜索树，通过自平衡机制，过渡到AVL树，通过绝对平衡，过渡到红黑树，一步接一步，把技术学到位。
 

---

二叉树框架

二叉树或者应该称为，二叉链表树。

• 每个节点都最多有两个叉的树
• 实现树的底层结构是链表

所以，二叉树和链表会有很多相同之处。

链表遍历框架：

class ListNode {
	int val;
	ListNode next;
}

void traverse( ListNode head ) {
	for( ListNode p = head; p != NULL; p = p.next )   // 迭代遍历
		do ···
}

void traverse( ListNode head ) {                      // 前序遍历
	print(head.val);
	traverse(head.next);
}

void traverse( ListNode head ) {                      // 后序遍历
	traverse(head.next);
	print(head.val);
}

二叉树遍历框架：

class TreeNode {
	int val;
	TreeNode left, right;
}

void traverse( TreeNode root ) {                       // 前序遍历
	print(root.val);
	traverse(root.left);
	traverse(root.right);
}

void traverse( TreeNode root ) {                       // 中序遍历
	traverse(root.left);
	print(root.val);
	traverse(root.right);
}

void traverse( TreeNode root ) {                       // 后序遍历
	traverse(root.left);
	traverse(root.right);
	print(root.val);
}

二叉树遍历框架拓展为多叉树遍历框架：

class TreeNode {
	int val;
	TreeNode[] children;
}

void traverse( TreeNode root ) {
	for( TreeNode child: root.children )
		traverse(child);
}

我们把这二叉树框架映入脑海里，下文的二分搜索树就是二叉树的延伸。
 

---

二分搜索树

数组的查找快，插入、删除慢，链表的插入、删除快，查找慢。

高效率的动态修改和高效率的静态查找，究竟能否同时兼顾？

通过对二分查找策略的抽象与推广，定义并实现二分搜索树结构，兼顾了：

• 链表插入的灵活性（直接插入即可，不需要挪动其他元素）
• 数组查找的高效性（二分查找）

插入、删除、查询操作均为 $O(log ~n)$。

实现二分搜索树，满足以下俩个条件：

• 若它的左子树不为空，左子树上所有节点的值都小于它的根节点。
• 若它的右子树不为空，右子树上所有的节点的值都大于它的根节点。

struct TreeNode {
	int val;
	TreeNode *left;
	TreeNode *right;
	
	TreeNode() : val(0), left(nullptr), right(nullptr) {}
	TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
	TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

 

---

验证

请打开题目：

• 验证二分搜索树的合法性：98. 验证二叉搜索树

按照二叉树框架：

void traverse( TreeNode root ) {                       
	/* 明确一个节点（root） 要做的事情 */

	// 其他部分，交给递归
	traverse(root.left);
	traverse(root.right);
}

按照二分搜索树的定义，一个节点自己要做的事情不就是比左孩子大，比右孩子小吗！

class Solution {
public:
    bool isValidBST(TreeNode* root) {
    	/* 明确一个节点（root） 要做的事情 */
		if( !root )                                         // 定义规定：空也是一颗二分搜索树
			return true;  
		if( root->left && root->val <= root->left->val )    // 定义规定：根节点 > 左孩子
			return false;
		if( root->right && root->val >= root->right->val )  // 定义规定：根节点 < 右孩子
			return false;

		// 其他部分，交给递归
		return isValidBST(root.left) && isValidBST(root.right);
    }
};

提交上去，发现居然不对。

二分搜索树的定义，不只是：

• 根节点 > 左孩子
• 根节点 < 右孩子

还有：

• 左子树上所有节点的值都小于它的根节点
• 右子树上所有的节点的值都大于它的根节点

比如：

10
   / \
  5   15
     / \
    6   20
P.S. 6 处于根节点的右子树，按照定义，凡右子树任何的子节点都要大于根节点 10

那么一个节点要做的事，不仅是和俩个孩子节点比较，还得和整个左子树、右子树的所有节点比较。

但其实我们也没必要和子树里面所有节点都比较，只需要知道一个子树的上界、下界，如果比较节点的值与 Min&Max，在范围外则 return false。

这个方法最关键的是理解对于每个节点来说，什么是他的 Min&Max。

以上图的树为例进行分析：

• 从 10 开始，因为是 root，所以可以为任何值。也就是在【Integer.MIN_VALUE, Integer.MAX_VALUE】范围内。
• 递归到 10 的右子树 15，15 的范围是多少呢？首先需要比 parent 要大，也就是 >10。上边界呢？没有改变，可以非常大，只要 >10 就行了。所以范围是【10+1，Integer.MAX_VALUE】。
• 递归到 15 的右子树 20，20 的范围是多少呢？首先需要比 parent 要大，也就是>15。上边界呢？没有改变，可以非常大，只要 >16 就行了。所以范围是【15+1，Integer.MAX_VALUE】。
• 递归到 15 的左子树 11，11 的范围是多少呢？首先需要比 parent 要小，也就是 <15。下边界呢？没有改变。所以范围是【11，15-1】。

class Solution {
public:
	bool isValidBST(TreeNode* root) {
    	return isValidBST(root, LONG_MIN, LONG_MAX);
    	// 使用 INT_MAX 会溢出，改用 LONG_MAX
  	}

	// 因为函数参数列表要增加参数，需要使用辅助函数
	bool isValidBST(TreeNode* root, long long min, long long max) {
    	if( !root )       // 节点为空，则说明一直到此的节点都在边界范围内，树没有问题
    		return true;
    
    	if( root->val <= min || root->val >= max )
        	return false;
        
    	return isValidBST(root->left, min, root->val) && isValidBST(root->right, root->val, max);
    	// 节点不是null，那么继续开始递归到左右子树（更新Min&Max）
    	// 并且只有他的左右子树都能通过测试时，这个节点才能通过测试。所以用 &&
    }
};

 

---

查找

按照二叉树框架：

void traverse( TreeNode root ) {                       
	/* 明确一个节点（root） 要做的事情 */

	// 其他部分，交给递归
	traverse(root.left);
	traverse(root.right);
}

在二分搜索树中查找一个数是否查找：

int target;
bool isInBST( TreeNode root ) {
	/* root 该做的事 */
	if( !root )
		return false;
	if( root->val == target )
		return true;

	// 递归框架
	return isInBST(root->left) || isInBST(root->right);
}

大框架是如此，此外 BST 还有 “左小右大” 的特点。

bool isInBST( TreeNode root, int target ) {
	/* root 该做的事 */
	if( !root )
		return false;
	if( root->val == target )
		return true;

	// 二分递归：一次排除一半
	if( root->val < target )
		return isInBST(root->right, target);
	if( root->val > target )
		return isInBST(root->left, target);
}

请打开题目：

• 700. 二叉搜索树中的搜索

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        return root->val > val ? searchBST(root->left, val) : searchBST(root->right, val);
    }
};

 

---

添加

在二分搜索树中插入一个数。

// 涉及到改，函数应该返回 TreeNode 类型，通过函数返回值接收
TreeNode insertIntoBST(TreeNode root, int val) {
	if( !root )                                             // 找到空位置
		return new TreeNode(val);                           // 插入新节点
	if( root->val == val )                                  // 已存在
		return root;							            // 不重复，直接返回
	if( root->val < val )						            // val 大
		root->right = insertIntoBST( root->right, val );    // 则插到右子树
	if( root->val > val )                                   // val 小
		root->left = insertIntoBST( root->left, val );      // 则插到左子树	
}

请打开题目：

• 701. 二叉搜索树中的插入操作

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {      // 俩个条件表达式嵌套
        return !root ? new TreeNode{val} : 
        (val < root->val ? root->left = insertIntoBST( root->left, val) : 
        root->right = insertIntoBST(root->right, val) , root);
    }
};

 

---

删除

先写出删除框架：

TreeNode deleteNode(TreeNode root, int key) {
	if( root->val == key )
		// 找到了，删除
	else if( root->val > key )	
		root->left = deleteNode(root->left, key);        // 去左子树寻找 key
	else if( root->val < key )
		root->right = deleteNode(root->right, key);      // 去右子树寻找 key
	return root;
}

删除有三种情况：

// 第一种：删除的是末端节点，没有孩子节点
if( !root->left && !root->right )
	return NULL;

// 第二种：待删除节点有一个子节点
if( !root->left )
	return root->right;
if( !root->right )
	return root->left;

// 第三种，待删除节点有俩个子节点，必须找到左子树最大节点，或者右子树最小节点，这里找右子树最小节点
if( root->left && root->right )
	TreeNode minNode = getMin(root->right);                   // 找到右子树的最小节点
	root->val = minNode->val;                                 // 最小节点上移到 root
	root->right = deleteNode(root->right, minNode->val);      // 删除最小节点

完整代码：

TreeNode deleteNode(TreeNode root, int key) {
	if( !root )
		return NULL;
	if( root->val == key ) {
		// 第二种：待删除节点有一个子节点，包含了第一种情况
		if( !root->left ) return root->right;
		if( !root->right ) return root->left; 
		
		// 左右孩子都存在，第三种情况
		TreeNode minNode = getMin(root->right);               // 找到右子树的最小节点
		root->val = minNode->val;                             // 最小节点上移到 root
		root->right = deleteNode(root->right, minNode->val);  // 删除最小节点
	}
			
	else if( root->val > key )	
		root->left = deleteNode(root->left, key);             // 去左子树寻找 key
	else if( root->val < key )
		root->right = deleteNode(root->right, key);           // 去右子树寻找 key
	return root;
}

TreeNode getMin(TreeNode node) {
	while( !node->left )                                      // 最左边的就是最小的
		node = node->left;
	return node;
}

无论是增、删、改、查：

• 二叉树的总体设计思路，把当前节点要做的事做好，其他的抛给递归框架，不用操心
• 如果当前节点会对下面的子节点有整体影响，可通过辅助函数增长参数列表，借助参数传递信息

请打开题目：

• 450. 删除二叉搜索树中的节点

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr)    
        	return nullptr;
        if (key > root->val)    
        	root->right = deleteNode(root->right, key);       // 去右子树删除
        else if (key < root->val)    
        	root->left = deleteNode(root->left, key);         // 去左子树删除
        else                                                  // 当前节点就是要删除的节点
        {
            if (! root->left)   
            	return root->right;                           // 情况1，欲删除节点无左子
            if (! root->right)  
            	return root->left;                            // 情况2，欲删除节点无右子
            TreeNode* node = root->right;                     // 情况3，欲删除节点左右子都有 
            
            while (node->left)                                // 寻找欲删除节点右子树的最左节点
                node = node->left;
            node->left = root->left;                          // 将欲删除节点的左子树成为其右子树的最左节点的左子树
            root = root->right;                               // 欲删除节点的右子顶替其位置，节点被删除
        }
        return root;    
    }
};

 

---

AVL平衡树

平衡树：对于任意一个节点，左子树与右子树的高度差不能超过 1。

所以，平衡树的成员还需要添加一个高度 height 以及计算出每个节点的平衡因子（左右子树高度差）是多少。

// 计算每个节点的平衡因子
int getBalanceFactor(TreeNode *root) {
	if( !root )
		return 0;
	return getBalanceFactor(root.left) - getBalanceFactor(root.right);
}

 

---

插入

在插入时，平衡树可能就不平衡了，失去树的优势，从树退化成链表。

如果该节点变得不平衡，则有 4 种情况：

• LL，插入在左侧的左侧
• RR，插入在右侧的右侧
• LR，插入在左侧的右侧
• RL，插入在右侧的左侧

1. 插入在左侧的左侧，导致高度差 > 1，需要右旋转

最简单的情况：

现在我们来讨论一下，通常的情况：

按照二分搜索树的特性：$T1<z<T2<x<T3<y<T4$，我们如果要改变树，也必须按照这个特性来平衡。整个右旋转过程如下（共 4 步）：

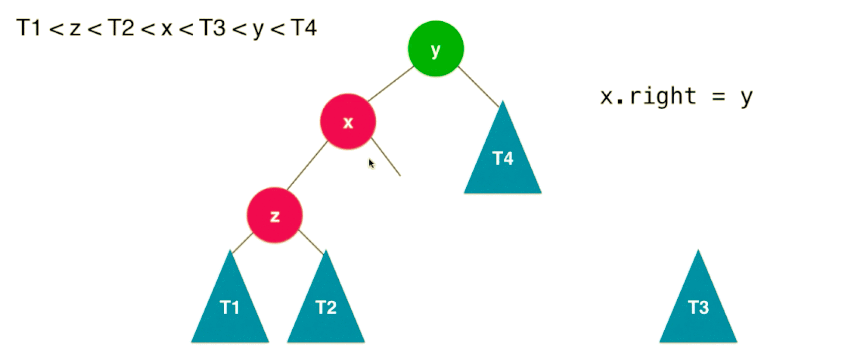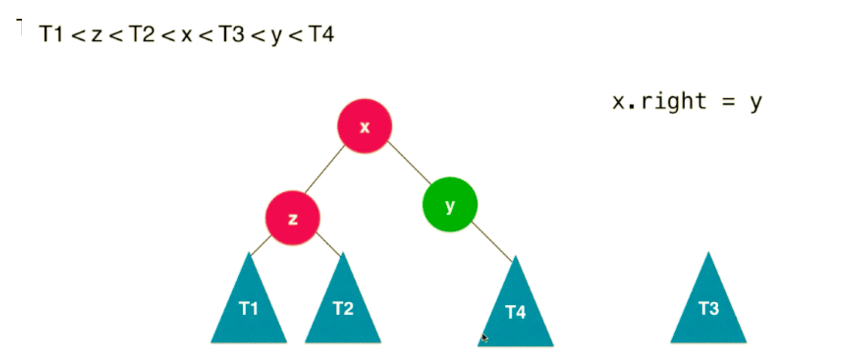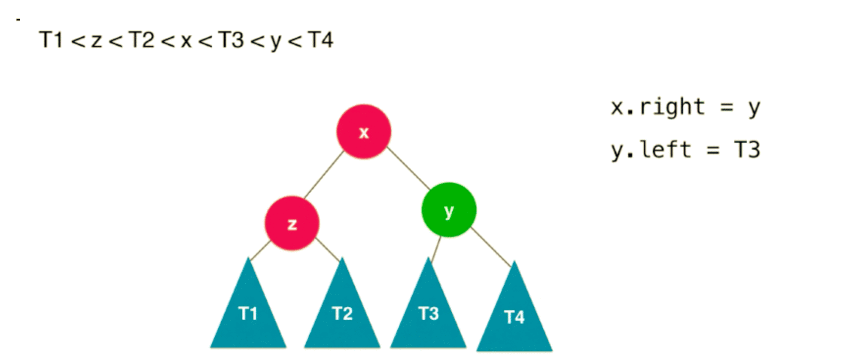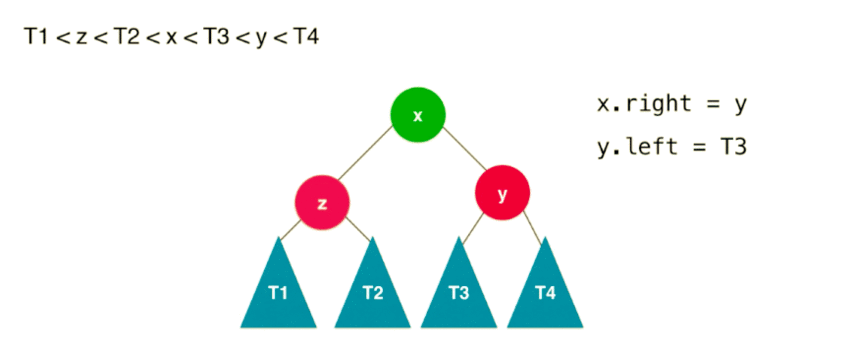
这个过程相对于，节点 y 顺时针的旋转到了节点 x 的右子树位置。

// 右旋转
Node *rightRotate(Node *y) {
	Node *x = y->left;
	Node *T2 = x->right;

	// 向右旋转过程
	x->right = y;
	y->left = T2;
	
	// 更新高度
	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;
	return x;
}

 
2. 插入在右侧的右侧，导致高度差 > 1，需要左旋转

过程推导如右旋转。

// 左旋转
Node *leftRotate(Node *x) {
	Node *y = x->right;
	Node *T2 = y->left;

	// 向左旋转过程
	y->left = x;
	x->right = T2;
	
	// 更新高度
	x->height = max(height(x->left), height(x->right)) + 1;
	y->height = max(height(y->left), height(y->right)) + 1;

	return y;
}

 
3. 插入在左侧的右侧，导致高度差 > 1，需要旋转

旋转后，就变成了左侧的左侧：

右旋转即可。

 
4. 插入在右侧的左侧，导致高度差 > 1，需要旋转

旋转后，就变成了右侧的右侧：

左旋转即可。

#include<bits/stdc++.h>
using namespace std;

class Node {
pubilc:
	int key;
	Node *left;
	Node *right;
	int height;
};

int height(Node *N) {
	if (N == NULL)
		return 0;
	return N->height;
}

int max(int a, int b) { return (a > b)? a : b; }

Node* newNode(int key) {
	Node* node = new Node();
	node->key = key;
	node->left = NULL;
	node->right = NULL;
	node->height = 1; 
	return(node);
}

// 右旋转
Node* rightRotate(Node *y) {
	Node *x = y->left;
	Node *T2 = x->right;

	// 向右旋转过程
	x->right = y;
	y->left = T2;
	
	// 更新高度
	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;
	return x;
}

// 左旋转
Node* leftRotate(Node *x) {
	Node *y = x->right;
	Node *T2 = y->left;

	// 向左旋转过程
	y->left = x;
	x->right = T2;
	
	// 更新高度
	x->height = max(height(x->left), height(x->right)) + 1;
	y->height = max(height(y->left), height(y->right)) + 1;

	return y;
}

int getBalance(Node *N) {
	if (N == NULL)
		return 0;
	return height(N->left) - height(N->right);
}

Node* insert(Node* node, int key) {
	if (node == NULL)
		return(newNode(key));

	if (key < node->key)
		node->left = insert(node->left, key);
	else if (key > node->key)
		node->right = insert(node->right, key);
	else               // 二分搜索树中没有重复元素
		return node;

	node->height = 1 + max(height(node->left), height(node->right));
	// 更新此祖先节点的高度

	int balance = getBalance(node);              
	// 得到这个祖先的平衡因子节点来检查这个节点是否成为不平衡的

	// 如果该节点变得不平衡，则有4种情况

	// 左侧的左侧
	if (balance > 1 && key < node->left->key)    // 左子树比右子树高 
		return rightRotate(node);                // 右旋转

	// 右侧的右侧
	if (balance < -1 && key > node->right->key)  // 左子树比右子树低 
		return leftRotate(node);                 // 左旋转

	// 左侧的右侧
	if (balance > 1 && key > node->left->key) {
		node->left = leftRotate(node->left);
		return rightRotate(node);
	}

	// 右侧的左侧
	if (balance < -1 && key < node->right->key) {
		node->right = rightRotate(node->right);
		return leftRotate(node);
	}
	return node;                                 // 返回（未更改的）节点指针
}

// 前序遍历
void preOrder(Node *root) {
	if(root != NULL) {
		cout << root->key << " ";
		preOrder(root->left);
		preOrder(root->right);
	}
}

int main() {
	Node *root = NULL;
	
	/* 构造平衡树 */
	root = insert(root, 10);
	root = insert(root, 20);
	root = insert(root, 30);
	root = insert(root, 40);
	root = insert(root, 50);
	root = insert(root, 25);
	
	preOrder(root);                            // 前序遍历
	return 0;
}

 

---

删除

平衡树的删除和二分搜索树一样：

1. 若为叶子节点，既没有左孩子节点也没有右孩子节点，直接删除；
2. 若只有一个孩子节点，则像链表一样将从其父节点和之间删除；
3. 若同时有左右孩子节点，按照中序遍历找出二叉树中比大的下一个节点（中序遍历下的后继节点），用其值代替，再继续用相同的规则递归的删除原始节点（实际上，中序遍历的后继节点不可能存在左孩子节点，要么无孩子节点，要么只有右孩子节点）；

不同的是，删除后，我们再让树保持平衡，此时也分 4 种情况：

• LL
• RR
• LR
• RL

删除完成后从的父节点开始依次向上，检查每个节点是否平衡，若不平衡则进行旋转操作，再更新节点高度，直到根节点。检查本身的时间复杂度为。

下图中删除节点，节点的中序遍历后继节点代替它，然后删除真正的。从新的开始检查每个节点是否平衡，直到根节点。本次删除结束。

Node* minValueNode(Node* node) {
	Node* current = node;

	/* 循环找到最左边的叶子 */
	while (current->left != NULL)
		current = current->left;

	return current;
}

Node* deleteNode(Node* root, int key) {
	if (root == NULL)
		return root;
	if ( key < root->key )
		root->left = deleteNode(root->left, key);
	else if( key > root->key )
		root->right = deleteNode(root->right, key);

	// 如果 key 与 root 的 key 相同，则是删除的节点
	else {
		// 只有一个子节点或没有子节点的节点
		if( (root->left == NULL) || (root->right == NULL) ) {
			Node *temp = root->left ? root->left : root->right;

			if (temp == NULL) {
				temp = root;
				root = NULL;
			} else 
				*root = *temp; 
			
			free(temp); temp = NULL;
		} else {
			Node* temp = minValueNode(root->right);      // 找到比待删除节点大的最小节点
			root->key = temp->key;                       // 用这个节点顶替待删除节点的位置
			root->right = deleteNode(root->right, temp->key);
		}
	}

	if (root == NULL)
	return root;

	root->height = 1 + max(height(root->left), height(root->right));
	
	int balance = getBalance(root);

	// 如果该节点变得不平衡，则有4种情况

	// Left Left Case
	if (balance > 1 && getBalance(root->left) >= 0)
		return rightRotate(root);

	// Left Right Case
	if (balance > 1 && getBalance(root->left) < 0) {
		root->left = leftRotate(root->left);
		return rightRotate(root);
	}

	// Right Right Case
	if (balance < -1 && getBalance(root->right) <= 0)
		return leftRotate(root);

	// Right Left Case
	if (balance < -1 && getBalance(root->right) > 0) {
		root->right = rightRotate(root->right);
		return leftRotate(root);
	}

	return root;
}

int main() {
	Node *root = NULL;

	root = insert(root, 9);
	root = insert(root, 5);
	root = insert(root, 10);
	root = insert(root, 0);
	root = insert(root, 6);
	root = insert(root, 11);
	root = insert(root, -1);
	root = insert(root, 1);
	root = insert(root, 2);

	preOrder(root);
	root = deleteNode(root, 10);
	preOrder(root);

	return 0;
}

 

---

左倾红黑树

红黑树比 AVL 树的实际性能更好，插入/删除次数上少一些，但也没有达到一个量级的碾压。

红黑树，依然是二分搜索树，也是一颗避免退化成链表的一种平衡树。

本文实现的是左倾红黑树，标准红黑树实现的一种。
 

---

2-3 树

要搞懂红黑树，就不得不先介绍 2-3 树。

2-3 树是一种多路树，其中所有非叶节点都有 2、3 个子节点。

2-3树，也满足二分搜索树的定义：

• 左孩子比 b 小
• 中间的孩子，在 b、c 俩者之间
• 右孩子比 c 大

2-3 树是绝对平衡树，绝对平衡，就是左右子树的高度差为 0，即高度相同。

这是怎么做到的呢？

插入 2-3 树从单个节点开始，在该节点中插入值直到它变满（3节点）

插满后，插入可能会导致分裂到根节点。

插入的下一个值将导致分裂为三个节点：

• 一个包含小于中值的值
• 一个包含大于中值的值
• 再将中值存储在父节点中

在拆分中插入 25 个结果：

绝对平衡的原因：

注意，左、右子树高度是绝对相同的（以下这种情况不可能）：

只会分裂成这个样子：

 

---

红黑树和 2-3 树的等价性

其实，哪怕我们让每个节点只存储一个元素，也可以实现这种绝对平衡。

这种树就是红黑树。

关键是 3 节点的实现，2-3 树的 3 节点，每个节点有 2 个元素。

而红黑树，每个节点只能有一个。

我们可以让俩个节点平行，如此就相对于 3 节点了。

逻辑关系如上，但物理实现却没有平行关系，节点 b 是节点 c 的左孩子。

但是为了体现平行关系，我们让：

• 2 节点的父/子值之间的链接用黑色链接表示
• 3 节点平行的节点内值之间的链接用红色链接表示

物理实现：

• 又因为二分搜索树的底层实现并没有边这个成员。
• 且每个节点只有一个父亲，父/子连接的边也只有一条边。

我们可以把这个边的信息存放在节点里面，比如让节点 b 变成红颜色：

红色节点表示和父亲节点是，平行关系。

把这个逻辑关系保存在节点上，而不是边上，就不需要添加特殊的边的代码。

具体来说 b < c，所有红色节点都是左倾斜的：

 如下图，把一颗 2-3 树转为红黑树：

这就是红黑树和 2-3 树等价关系，红黑树引入红色节点相对于2-3树的平行关系。

 

---

基本性质

红黑树结构：

#define RED 'R'
#define BLACK 'B'

struct RbNode {
public:
  char color;
  int value;
  RbNode *left;
  RbNode *right;
};

基本性质：

• 根节点是黑
• 每个节点或者红、或者黑
• 每一个叶子节点，是黑
• 如果一个节点是红，孩子节点一定是黑
• 从任意一个节点到叶子节点，经过的黑色节点是一样的

绝对平衡的性质，就让 2-3 树从任意一个节点到叶子节点，经过的节点数是一样多的。

对应到红黑树，就是所对应的黑色节点是一样多的。

所以，红黑树的最大高度是 $2log~n$。

• $log~n$：是树的高度
• $2log~n$：是因为3节点的黑色节点有一个红色节点
   

---

插入

回顾一下，2-3 树添加元素过程。

2-3 树添加一个新的元素，也是按照二分搜索树的策略查找插入位置，但永远不会添加到一个空的位置，只会融合进已有的节点中，去找到的最后一个叶子节点去融合：

• 如果找到的叶子节点是 2- 节点，就形成一个 3- 节点
• 如果找到的叶子节点是 3- 节点，暂时形成一个 4- 节点

解释一下：

• 2- 节点，一个父节节点，俩个孩子节点
• 3- 节点，俩个父亲节点，三个孩子节点
• 4- 节点，三个父亲节点，四个孩子节点

红黑树，红节点相对于 3- 节点俩个元素中最左侧的那个元素 b，代表这个节点和父节点是平行的（3-节点）。

因为这个原因，所以红黑树添加元素，这个新添加的节点永远是一个红色的节点。

当然，在红黑树中添加节点，可能会导致平衡被破坏，我们需要做相应的平衡机制。

······

红黑树的插入过程与AVL树类似，按照二分查找找到适合的位置插入新节点 x ，然后从 x 沿着父节点向上对每个节点检查，若红黑树的属性被破坏则通过以下规则调整自己。

平衡调整规则：

• LL
• RR
• LR
• RL

这四种旋转和 AVL 树的旋转操作其实是一样的，不过要对节点的颜色进行更新。

几种需要进行调整平衡的情况：

1. 情况一：红黑树为空，添加的节点（根节点）为红色

红黑树开始为空的时候，添加第一个节点，这个节点是红色的。

新插入节点都为红色，但红黑树定义是根节点必须为黑色，我们需要染成黑色。

 

2. 情况二：待插入元素大于父亲节点（添加在右边），需要左旋转

根节点 42，待插入元素 37 比 42 小，那么插在左侧，不需要调整就是一颗红黑树。

但如果待插入元素大于父亲节点，就需要调整。

根节点是 37，待插入元素 42 比 37 大：

但红黑树定义，所有红色节点都是向左倾斜，这时候就需要左旋转。旋转过程：

二分搜索树的旋转过程完成，但还需要检测一下颜色是否符合红黑树定义。原来未旋转前 node 是根节点，原来节点是什么颜色，那 x 就是什么颜色：

对于 node 颜色要变成红色，因为新加入节点 42 和 node 37 形成了一个 3- 节点，为了表示平行关系，node 需要染红：

以上，是红黑树的左旋转过程。

Node* leftRotate(Node* node){
	Node* x = node->right;

	// 左旋转
	node->right = x->left;
	x->left = node;

	// 更新颜色
	x->color = node->color;
	node->color = RED;
	return x;
}

 

3. 往 3- 节点中插入，插在右侧，需要做颜色翻转

根节点 42、左孩子 37，待插入元素 66 比 42 大，那么插在右侧

2-3 树，插入的下一个值将导致分裂为三个节点：

• 一个包含小于中值的值
• 一个包含大于中值的值
• 再将中值存储在父节点中

这就相对于 2-3 树中的 4- 节点（ 37\42\66 ），会拆分成 3 个 2- 节点。

3 个 2- 节点在红黑树中，都是黑节点，所以我们要把 37、66 染黑。

一个临时的 4- 节点拆分后，根节点要向上和它的父节点做融合。

融合意味着，新的根节点 42 要变成红色节点。

这个过程，没有调整元素位置，只是改变了颜色，也叫颜色翻转。

// 颜色翻转
void flipColors(Node* node){
	node->color = RED;
	node->left->color = BLACK;
	node->right->color = BLACK;
}

 

4. 往 3- 节点中插入，插在左侧，需要右旋转

根节点 42、左孩子 37，待插入元素 12 比 42 小，那么插在左侧

相对于：

node 节点需要右旋转：

二分搜索树的旋转过程完成，但还需要检测一下颜色是否符合红黑树定义。

原来未旋转前 node 是根节点，原来节点是什么颜色，那 x 就是什么颜色：

现在 node 节点是 x 的右孩子，此时 12/37/42 对应到 2-3 树中，还是一个临时的 4- 节点：

所以，要让 node 变成红色，表示它和父亲节点融合在一起的。

Node* rightRotate(Node* node){
	Node* x = node->left;

	// 右旋转
	node->left = x->right;
	x->right = node;

	// 更新颜色
	x.color = node->color;
	node->color = RED;
	return x;
}

 

红黑树所有插入情况一览：

其实 3- 节点的 3 种情况可以浓缩成 1 个逻辑链条：

• 如果新添加的元素，比初始的俩个节点都小，就相对于跳到第 3 图：

• 如果新添加的元素，比初始的俩个节点都大，就相对于跳到第 4 图：

 

---

删除

红黑树删除一个节点比添加一个节点，还要复杂。

• 前半部分与 AVL 树相同
• 删除完节点之后，递归向上，按照 5 种调整情况进行调整。

 

---

白板编程红黑树

一谈数据结构，就很容易问到红黑树。

如图，面试时在白板上手写红黑树，谁写的出来，谁是大佬……

但说实话，红黑树编程实现特别繁琐，操作过于复杂。

动不动上百行，红黑树大概是，最不适合白板编程问题之一。

考察红黑树的底层实现，几乎就是考察面试者是否在面试前记忆红黑树而已。

真正面试的是思路，都是从一个很平常的问题开始。

比如快速排序。

■ 子过程 partition 是：给定一个数组，选定其中一个值。如何把这个数组分成两部分，一部分小于这个值，一部分大于这个值？

■ partition 操作就有很多实现方式，单路，双路，再到三路快排。如果能一路优化下来，并且明确每次优化的目的是什么，就已经很可以看出面试者的水平了。

■ 快排的思路还可以解决“快速查找第k大的数字”这个经典问题。

■ 同时，快速排序本质是一个随机算法，因为在partition的过程中，pivot选择需要随机。这样也可以引出一些和随机算法相关的问题。

拓展性极好，而且白板编程在十行、二十行内。

面试刷题是否有用？

首先，通过刷题复习一下所学的计算机知识还是有用的，但是，如果仅仅是记住面试题的答案，而没有搞清楚对方出这道题的原因，通常过不了面试关。

比如一道经典的面试题可以用很多年，很多人都见过，但是90%的候选人依然无法回答得很完美，因为关于那道题有太多的坑，除非对计算机算法、组合数学或者通信有透彻的理解，否则无法回答得完美。

透过那道题，就能看清一个人解决问题的思路和应用所学知识的水平。