在开始之前,我们需要导入NumPy和Matplotlib两个库。导入过程可以通过以下代码来完成:
import numpy as np
import matplotlib.pyplot as plt
% matplotlib inline
本章给出的例子与Cameron Davidson Pilon在2015年出版的Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference一书中所给的例子类似。但是,我们的例子被重新编写以更加适配金融背景,书中的数学概念也可以从代码中更直观的体现。
假设你有一种证券,它要么值1美元,要么一文不值。收益取决于两步:(1)证券的收益随机,其概率为50%。在收益随机的情况下,50%可能获得1美元收益,50%收益为0;(2)证券拥有真正的收益,其概率也为50%。在这种情况下,获得1美元收益的概率
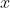
,称为真正收益概率(True Payoff Probability,TPP)。
这个收益方案如图10.1所示。

图10.1 收益方案
你更感兴趣的是找出真正的收益率是多少,因为真正的收益率将会告诉你采取什么交易策略。在本例中,你购买100股证券,在这100股证券中,有54股让你赚了1美元。
实际的TPP是多少呢?在本例中,可以通过给出解析解来分析最可能的TPP。但是我们将使用一种适用于更复杂问题的计算方法。
在第10.1.1节中,我们将证券收益过程进行模拟。
10.1.1 扁平先验
变量
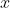
表示TPP。我们随机采样100个真值;如果你在真正收益情况下获得了1美元,则该真值为1,否则为0。我们在图10.1的受益方案中,在“开始”和“随机收益率”两个过程也进行随机抽样。尽管有的时候并不是全都需要,但对所有试验一口气全部采样的随机结果在计算效率上更高效。
最后,我们将所有收益相加,然后除以证券的数量,最终我们求的是本次仿真试验中的收益率。
下面的代码段是仿真运行函数。然而,你需要确保能够理解计算过程是如何与图10.1的方案对应的,这是非常重要的事情。[1]
def run_sim(x):
truth = np.random.uniform(size=100) < x
first_random = np.random.randint(2,size=100)
second_random = np.random.randint(2,size=100)
res = np.sum(first_random*truth +(1-first_random)*second_random)/100
return res
接下来,我们想试验一些可能的TPP。因此,本例将对一个候选TPP进行抽样,并使用此概率进行模拟。如果仿真输出的收益与我们在现实生活中观察到的收益相同,那么这个候选TPP就是一个真实概率。
下面的采样函数将返回真实概率。当候选概率与输入不等的时候,返回None:
def sample(data = 0.54):
x = np.random.uniform()
if run_sim(x) == data:
return x
由于需要对可能的TPP进行抽样,因此我们很自然地希望能加快这一过程。为此,我们使用JobLib的库,采用并行执行的方式来加速上述计算过程。
提示:
JobLib在Kaggle内核上已经预安装。
我们需要导入Parallel类和delayed方法。Parallel类将有助于并行地执行这些循环,delayed方法则有助于在并行循环内按顺序执行相应函数。通过以下代码来导入它们:
from JobLib import Parallel, delayed
上述Parallel类和delayed方法的具体细节与本例无关。Parallel(n_jobs=-1)方法使任务的并行执行数量与机器上的CPU数量相同。例如,delayed(sample)() for i in range(100000) 代码中sample方法将执行100000次。[2]
我们获得Python列表t,并将其转换为一个NumPy数组。正如你在以下代码段中看到的,数组中大约有98%的值为None。这意味着在采样器测试的
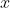
值中,有98%与我们的数据不匹配。
t = Parallel(n_jobs=-1)(delayed(sample)() for i in range(100000))
t = np.array(t,dtype=float)
share = np.sum(np.isnan(t))/len(t)*100
print(f'{share:.2f}% are throwaways')
98.01% are throwaways
因此,我们现在将丢弃所有None值,留下
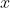
值:
t_flat = t[~np.isnan(t)]
plt.hist(t_flat, bins=30,density=True)
plt.title('Distribution of possible TPPs')
plt.xlim(0,1);
运行上述代码后,我们将得到如图10.2所示的输出。
正如你所看到的,图10.2展示了可能的TPP分布情况。这张图显示,TPP最可能的范围是50%~60%。虽然其他值也是有可能的,但它们的可能性更小。
你刚才看到的是贝叶斯方法的优点之一。所有的估计以分布形式展示,我们可以计算置信区间(在贝叶斯术语中称为“可信区间”)。

图10.2 朴素采样器发现的可能真实收益概率的分布
这让我们能够对事情的确信度更加精确,也让模型中其他参数值的可能性更加精确。将它与我们感兴趣的金融领域联系起来。在金融应用中,数以百万美元的金钱都按照模型输出进行交易,因此能够量化这种不确定性就是非常大的优势。
10.1.2 < 50%先验
此时,你可以将结果提交给证券交易领域的一名专家,他看了你的分析,摇了摇头说:“TPP不能超过0.5。”他解释道,“从基础业务来看,这在客观上不可能超过50%。”
那么,你将如何把这个事实融合到仿真分析中呢? 最直接的解决方案是仅试验从0到0.5的候选TPP。你所需要做的就是限制候选
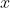
的采样空间。可以通过运行以下代码来实现:
def sample(data = 0.54):
x = np.random.uniform(low=0,high=0.5)
if run_sim(x) == data:
return x
现在,你可以像刚才那样进行仿真了:
t = Parallel(n_jobs=-1)(delayed(sample)() for i in range(100000))
t = np.array(t,dtype=float)
# Optional
share = np.sum(np.isnan(t))/len(t)*100
print(f'{share:.2f}% are throwaways')
99.10% are throwaways
t_cut = t[~np.isnan(t)]
plt.hist(t_cut, bins=15,density=True)
plt.title('Distribution of possible TPPs')
plt.xlim(0,1);
像前面那样,上面代码将输出图10.3所示的结果。

图10.3
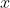
从0~0.5区间下潜在TPP分布
10.1.3 先验与后验
显然,你选择的值会影响仿真分析的结果,这也反映出你对
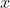
可能的值的认识。
在第一轮中,在你看到任何数据之前,认为所有介于0和100%之间的TPP都是等概率的,这被称为“扁平先验”,因为所有值的分布都是相同的,因此是扁平的。在第二轮中,你认为TPP必须低于50%。
在看到数据之前能表示你对
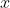
认识的分布称为“先验分布
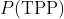
”,简称“先验”。我们从仿真中得到的可能
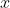
的分布(也就是看到数据
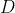
后)称为“后验分布
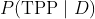
”,简称“后验”。
以下代码给出了第一轮和第二轮的先验和后验采样情况。首先是绘制扁平后验的结果,运行如下代码:
flat_prior = np.random.uniform(size=1000000)
plt.hist(flat_prior,bins=10,density=True, label='Prior')
plt.hist(t_flat, bins=30,density=True, label='Posterior')
plt.title('Distribution of $x$ with no assumptions')
plt.legend()
plt.xlim(0,1);
上述代码生成图10.4。

图10.4 扁平先验的采样结果
接下来是对小于50%先验的采样输出。运行如下代码:
cut_prior = np.random.uniform(low=0,high=0.5,size=1000000)
plt.hist(cut_prior,bins=10,density=True, label='Prior')
plt.hist(t_cut, bins=15,density=True, label='Posterior')
plt.title('Distribution of $x$ assuming TPP <50%')
plt.legend()
plt.xlim(0,1);
上述代码生成图10.5。尽管使用了相同的采样器,但你可以看到结果是非常不同的。

图10.5 对小于50%先验的采样结果
你注意到什么奇怪的事情了吗?第二轮的后验值大致等于第一轮的后验值,但第二轮后验值在0.5处被截断了。这是因为第二轮试验中当
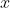
大于0.5的时候,它的先验值为0,对于其他值为1。
由于我们只记录与数据相匹配的仿真结果,因此直方图中显示的仿真结果反映了在给定TPP和
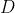
的情况下,运行仿真试验并输出观察数据
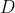
的概率
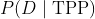
。
从仿真试验得到的后验概率
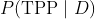
等于在给定某个TPP情况下进行试验并观察到数据的概率
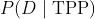
乘以概率
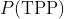
。
数学上,上述关系表示为:
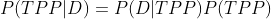
当数据可以通过诸如面对面会议等方式自然地获取时,那么我们可能需要说明数据收集方法中存在的偏见。大多数情况下,我们不必担心这个问题,可以简单地忽略它。但有些时候,这种测量能够放大某些结果。
为了缓解这个问题,我们需要除以数据分布
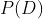
将其作为后验公式的最后补充,并得到如下公式:
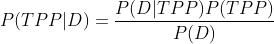
如你所见,这就是贝叶斯公式!当我们做仿真试验时,是从后验中采样。为什么不能直接用贝叶斯公式来计算后验呢?答案很简单,计算
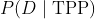
需要我们对TPP进行积分。这个计算是非常棘手的。我们的仿真方法是一种简单方便的替代解决方案。
提示:
第一轮先验(即所有的TPP都是等可能的)称为扁平先验,因为我们对TPP值的分布不做任何假设。在这种情况下,贝叶斯后验等于最大似然估计。
10.1.4 马尔可夫链蒙特卡罗算法
在第10.1.3节中,我们通过从先验中随机采样,然后试验采样值来近似估计后验分布。这种随机试验的方法在模型只有一个参数(比如TPP)时效果会很好。然而,随着模型复杂度的提高和参数的增加,随机搜索方法将变得更慢。最终,将可能有太多的参数组合没有机会生成数据。因此,我们需要频繁地指导搜索操作并使用更高的后验概率来采样参数。
这种有指向性但仍然随机的采样方法被称为马尔可夫链蒙特卡罗算法。蒙特卡罗表示随机和仿真,马尔可夫链表示我们在参数空间上以某些概率进行搜索。
在这里讨论的特定算法中,我们将以一定的概率采用一个不同的参数值,这个概率是该参数值的后验概率的比率。这里,我们将考虑计算参数值的后验概率。由于概率不能大于1,我们将把比率限制在1以内。但这只是一个数学上的限制,对算法来说并无太大影响。
图10.6展示了马尔可夫链蒙特卡罗算法的基本工作原理。

图10.6 马尔可夫链蒙特卡罗算法
图10.6显示我们处于“随机行走”中,或多或少地随机遍历不同的参数值。然而,实际上我们并不是完全“随机移动”,而是更倾向于具有更高后验概率的参数值。
为了执行这个算法,我们需要做4件事。
1.从当前参数值
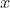
处提出一个新的参数值
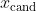
。
2.使用贝叶斯法则来估计参数
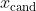
的后验概率
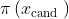
。
3.计算从
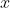
移动到新参数值
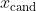
的概率
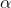
。(注意概率必须小于1。)
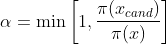
4.以概率
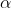
转移到新的参数值。
接下来,我们逐步构建这个算法的模块:
# REPETITION FROM FIRST SECTION
def run_sim(x):
truth = np.random.uniform(size=100) < x
first_random = np.random.randint(2,size=100)
second_random = np.random.randint(2,size=100)
res = np.sum(first_random*truth +(1-first_random)*second_random)/100
return res
# REPETITION FROM FIRST SECTION
def sample(x,data = 0.54):
if run_sim(x) == data:
return x
首先,我们需要设置一个新的
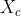
。由于我们不想盲目地随机搜索,而是更精确地随机游走,因此设置
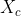
需要依赖于
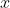
的先前值。在本例中,我们将从均值为
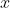
、标准差为0.1的正态分布中采样
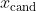
。
只要满足
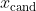
与
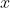
是相关的条件,从其他分布或具有不同标准差的正态分布中取样也是可以的:
def propose(x):
return np.random.randn() * 0.1 + x
在本章第一部分内容中,我们通过从先验中采样然后通过运行仿真程序的方法来实现直接从后验中采样。现在,我们通过马尔可夫链蒙特卡罗算法来采样,这样就不再直接从后验采样。因此,可以使用贝叶斯法则来计算后验概率。
记住通常不除以
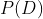
,因为我们不假设有偏测量。贝叶斯法则可以简化为
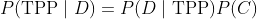
,其中
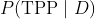
为后验概率,
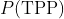
为先验概率,
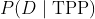
为似然值。因此,为了估计参数
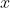
的似然值,我们使用该参数进行了多次仿真试验。
似然值是仿真试验匹配真实数据的比例:
def likelihood(x):
t = Parallel(n_jobs=-1)(delayed(sample)(x) for i in
range(10000))
t = np.array(t,dtype=float)
return (1 - np.sum(np.isnan(t))/len(t))
我们首先再次使用扁平先验计算,也就是每个TPP都是等概率的:
def prior(x):
return 1 #Flat prior
参数
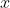
的后验概率为似然值乘以先验概率:
def posterior(x):
return likelihood(x) * prior(x)
现在,我们准备将上面所有内容整合到Metropolis-Hastings MCMC算法中。
首先,我们为
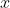
设置初始值。为了让算法快速找到可能的值,明智的做法是将
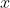
初始化为最大似然值或我们认为可能的某个估计值。如果要计算这个初始值的后验概率,运行以下代码即可:
x = 0.5
pi_x = posterior(x)
同样,需要记录试验中采样的所有值。为了展示,我们也跟踪记录了后验概率。运行以下代码:
trace = [x]
pi_trace = [pi_x]
现在,我们进入主循环。在此之前,我们需要记住算法包含4个步骤:
1.设置新的候选
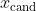
;
2.计算后验概率
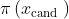
;
3.计算接受概率:
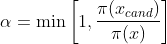
4.以概率
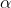
来设置
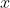
为
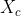
。
for i in range(1000): #Main Loop
x_cand = propose(x)
pi_x_cand = posterior(x_cand)
alpha = np.min([1,pi_x_cand/(pi_x + 0.00001)]) # Save division
u = np.random.uniform()
(x, pi_x) = (x_cand,pi_x_cand) if u<alpha else (x,pi_x)
trace.append(x)
pi_trace.append(pi_x)
if i % 10 == 0:
print(f'Epoch {i}, X = {x:.2f}, pi = {pi_x:.2f}')
Epoch 0, X = 0.50, pi = 0.00
Epoch 10, X = 0.46, pi = 0.04...
Epoch 990, X = 0.50, pi = 0.06g
在运行这个算法若干轮后,我们最终得到一个潜在作弊者收益份额的分布。跟之前所做的一样,运行以下代码使结果可视化:
plt.hist(trace,bins=30)
plt.title('Metropolis Hastings Outcome')
plt.xlim(0,1);
结果如图10.7所示。

图10.7 Metropolis Hastings采样器的输出
通过查看trace随时间变化的轨迹,trace数据显示了算法是如何以高度可能的值为中心进行随机移动的:
plt.plot(trace)
plt.title('MH Trace');
我们将以图表形式获得输出结果如图10.8所示,该结果向我们展示了Metropolis Hasings采样器的运行轨迹。

图10.8 Metropolis Hastings采样器的轨迹
为了更好地理解,我们绘制了后验概率随所试验值变化的情况:
plt.scatter(x=trace,y=pi_trace)
plt.xlabel('Proposed X')
plt.ylabel('Posterior Probability')
plt.title('X vs Pi');
成功执行代码后,我们将得到图10.9所示的输出图像。

图10.9 试验值和后验概率
10.1.5 Metropolis-Hastings MCMC
为了展示PyMC3的强大功能和灵活性,我们将它用于一个经典的计量经济学问题,但重点要从贝叶斯角度对其进行阐述。
提示:
本例直接改编自PyMC3文档中的示例,而PyMC3文档中的例子改编自霍夫曼论文“No-U-Turn Sampler”。
股票价格和其他金融资产价格都波动,日收益的方差被称为波动率。波动率是一种常用的风险评估方法,因此对其进行准确的度量是非常重要的。
简单的解决方案是计算收益的事后风险度量,即方差。但是,表达实际收益波动率的不确定性是有益的。与我们之前看过的收益例子类似,这里存在一个实际值的分布,从这个分布中可以得到已实现的值。因为存在可能的波动率值的分布,其中观察到的波动率可能就是一个已实现的样本,这也称为“随机波动率”。
在本例中,我们建立标准普尔500指数的随机波动率模型。为此,我们首先加载数据,你可以直接从互联网下载数据,也可以在Kaggle平台上找到数据。
运行以下代码加载数据:
df = pd.read_csv('../input/S&P.csv')
df['Date'] = pd.to_datetime(df['Date'])在这个例子中,我们对收盘价感兴趣,因此需要从数据集中提取收盘价。数据集先显示新的数据。因此需要将其反转,通过以下代码实现:
close = pd.Series(df.Close.values,index=pd.DatetimeIndex(df.Date))
close = close[::-1]
以下代码绘制了收盘价。
close.plot(title='S&P 500 From Inception');
SP500
我们将获得图10.10所示的图表。

图10.10 从股市开市以来到2018年S&P500收盘价
数据集包含了标准普尔自开市以来的数据,这对我们来说有点太多了。所以在本案例中,我们将其在1990年截断。通过运行下列代码来指定这个时间:
close = close['1990-01-01':]
由于我们对收益感兴趣,因此需要计算价差。我们使用np.diff来获取每日价差。为了便于画图,我们将每日价差结果用pandas Series对象来存储:
returns = pd.Series(np.diff(close.values),index=close.index[1:])
returns.plot();
输出结果如图10.11所示。

图10.11 从1990年到2018年的S&P500的收益
PyMC3包含一些处理时间序列所需的特殊分布,如随机游走。当我们想要对股票价格进行建模时,使用PyMC3是非常正确的方法。
首先,导入PyMC3及其时间序列工具random walk类:
import pymc3 as pm
from pymc3.distributions.timeseries import GaussianRandomWalk
然后,建立模型,可以运行以下代码来实现建模:
with pm.Model() as model:
step_size = pm.Exponential('sigma', 50.) #1
s = GaussianRandomWalk('s', sd=step_size, #2
shape=len(returns))
nu = pm.Exponential('nu', .1) #3
r = pm.StudentT('r', nu=nu, #4
lam=pm.math.exp(-2*s),
observed=returns.values)
现在让我们回顾下建模需要执行的代码命令。如你所见,它有4个关键要素组成。
1.波动率

被建模为随机游动过程,该随机游走的步长为step_size。步长的先验分布是
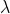
= 50的指数分布。(再次说明,理解所使用的每个分布的细节知识对于演示和试验来说并不是必需的。)
2.然后对随机波动率本身进行建模。由于步长本身就是一个随机变量,请注意我们是如何将步长融入随机波动率模型中的。随机游走的长度应与观察到的收益值相同。
3.我们建立了满足nu个自由度的StudentT分布的实际股票收益模型。nu的先验也是指数分布。
4.最后,我们对实际收益进行建模。将实际收益建模成比例因子为lam的StudentT分布,其中lam是由随机波动模型生成的。为了使模型基于观察到的数据进行构建,我们将观察的收益值作为参数传入模型中。
PyMC3的标准采样器不是Metropolis Hastings,而是No-U-Turn采样(No-U-Turn Sampler,NUTS)。如果我们不指定采样器而仅调用sample,则PyMC3将默认为NUTS。
为了使采样平稳运行,需要指定较大量的tune采样。采样器将会从这些tune采样中抽取样本,以便找到一个好的起点。类似于之前的burned采样,这些tune采样也不会成为后验中的一部分。
我们需要设置较高的target_accept值,来告诉NUTS在接受值时要宽容。可以运行以下代码来实现:
with model:
trace = pm.sample(tune=2000,nuts_kwargs=dict(target_accept=.9))
PyMC3有一个很好用的工具,它可用于可视化采样结果。我们对波动率随机游动的标准偏差
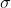
以及实际收益所符合的StudentT分布的自由度比较感兴趣。
在并行运行两段代码时,你可以看到两个不同的输出分布。如果我们将采样器运行更长的时间,那么这两个结果将会收敛。可以通过对它们进行平均来获得更好的估计,这就是PyMC3针对预测所采用的方法。现在让我们尝试使用以下代码:
pm.traceplot(trace, varnames=['sigma', 'nu']);
TracePlot
图10.12显示了该代码的执行结果。

图10.12 PyMC3采样器的结果概览(左侧两个采样器生成的分布,右侧是它们的轨迹)
在最后一步,我们展示了随机波动率是如何随时间变化的。你可以看到它是如何与经济波动周期(例如2008年金融危机)完美契合的。你还可以看到,在某些时期中,模型对波动率大体是确定的:
plt.plot(returns.values)
plt.plot(np.exp(trace[s].T), 'r', alpha=.03);
plt.xlabel('time')
plt.ylabel('returns')
plt.legend(['S&P500', 'Stochastic Vol.']);
该代码的输出如图10.13所示。

图10.13 1990年至2018年的推断随机波动率
有大量的应用可以使用此类相对小规模的贝叶斯模型来进行建模,其主要优点是模型易于解释并且可以很好地表达不确定性。由于模型很清楚地表述了需求,因此概率编程与数据科学中的“storytelling”方法很一致。
在第10.1.6节中,我们将从浅层概率编程转向深层概率编程。
10.1.6 从概率编程到深度概率编程
到目前为止,我们开发的贝叶斯模型都很浅。因此,我们要考虑是否可以将深度网络的预测能力与贝叶斯模型的优势相结合,这是一个活跃的研究领域。
深度网络具有大量参数,这使得在参数空间中搜索成为难题。在传统的监督深度学习中,我们使用反向传播来解决这个问题,反向传播也可以用于贝叶斯模型。但是,它不是进行贝叶斯深度学习的唯一方法,甚至不一定是最佳方法。
总体来说,有4种方法可以用于贝叶斯深度学习。
- 使用自动微分变分推理(Automatic Differentiation Variational Inference,AVI)。这意味着用引导模型来近似后验分布,然后使用梯度下降来优化模型参数。PyMC3使用AVI优化器可以实现这一点。请参阅Alp Kucukelbir等人于2016年发表的论文“Automatic Differentiation Variational Inference”。或者,你可以使用Pyro,它实现了快速的、GPU优化的AVI。尽管在这里不适合花大量篇幅介绍PyMC3,但还要推荐PyMC3文档,它是一个很好的教程。
- 假设后验值呈正态分布,然后使用标准神经网络库(例如Keras)并学习每个参数的均值和标准差。还记得我们在使用变分自编码器时如何从参数化正态分布中采样值吗?我们可以对每一层都这样做。与AVI相比,这种方法训练速度更快,占用的计算资源和内存更少,但灵活性较差,其参数是非贝叶斯神经网络的两倍。
- 使用dropout技巧。在使用时间序列时,我们在测试时间打开了dropout功能,并多次运行推理以获得置信区间。这是一种非常容易实现的贝叶斯学习,没有比常规神经网络更多的参数。但是,它在推理时速度较慢,并且也不具有AVI的所有灵活性。
- 挑选并混合。为了训练神经网络,我们需要一个可以从AVI获得的梯度信号。我们可以以常规方式训练神经网络的socket(有时我们称之为“特征提取器”),并以贝叶斯方式训练网络的头部。这样,我们可以获得不确定性估计,而不必承担贝叶斯方法的全部成本。
本文摘自:《金融中的机器学习》

机器学习是设计与应用算法的科学,可从数据中进行学习和预测,其应用已经非常普遍。金融领域集中了大量的交易数据,为人工智能技术的运用奠定了良好的数据基础。本书面向金融领域的读者,介绍了机器学习技术的原理与实践。
本书包括10章,介绍了神经网络算法、结构化数据的处理、计算机视觉处理技术、时间序列分析、自然语言处理、生成模型的应用、强化学习技术、数据建模与调试、贝叶斯推理和概率编程等内容。
本书由资深金融从业者编写,融合了其在金融项目中关于机器学习的实践经验,适合金融领域的数据科学家、数据分析师、金融科技公司的技术研发人员以及对金融领域的机器学习技术感兴趣的读者阅读。























