一、 Scipy模块
开源科学库,SciPy一般都是操纵NumPy数组来进行科学计算,统计分析,可以说是基于NumPy之上。SciPy提供了许多科学计算的库函数,包含的功能,最优化、线性代数、积分、插值、拟合、特殊函数、快速傅里叶变换、信号处理、图像处理、常微分方程求解器,系数矩阵计算等,
- 应用场景:Scipy是高端科学计算工具包,用于数学、科学、工程学等领域
- 安装 pip install scipy
""" 包含子模块
cipy.cluster向量计算
Kmeansscipy.constants物理和数学常量
scipy.fftpack傅立叶变换
scipy.integrate积分程序
scipy.interpolate插值
scipy.io数据输入输出
scipy.linalg线性代数程序
scipy.ndimagen维图像包
scipy.odr正交距离回归
scipy.optimize优化
scipy.signal信号处理
scipy.sparse稀疏矩阵
scipy.spatial空间数据结构和算法
scipy.special一些特殊的数学函数
scipy.stats统计
"""二 、概率密度
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']#用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False#用来正常显示负号
#正态分布概率密度
X = []
Y = []
for a in np.linspace(-5, 5, 100):
y = stats.norm.pdf(a)
X.append(a)
Y.append(y)
plt.plot(X, Y)
plt.xlabel("x")
plt.ylabel("p")
plt.title("正态分布概率密度")
plt.show()三、正态分布查表
正态分布查表其实就是查累积概率分布。
设某校学生身高服从均值为160, 方差为3600的正态分布,那该校学生身高在180以下的学生比例是多少?
转换为标准正态分布,
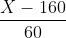
服从标准正态分布,
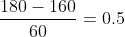
,于是我们查标准正态分布表0.5的值,用
scipy.stats.norm.cdf(0.5)
from scipy import stats
p = stats.norm.cdf(0.5)
print(p)四、常用统计方法
from scipy.stats import chi2 # 卡方分布
from scipy.stats import norm # 正态分布
from scipy.stats import t # t分布
from scipy.stats import f # F分布
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.stats as stats
from scipy.stats import chi2_contingency # 列联表分析
# matplotlib画图注释中文需要设置
from matplotlib.font_manager import FontProperties
xy_font_set = FontProperties(fname=r"c:\windows\fonts\方正稚艺简体.ttf", size=12)
zhushi_font_set = FontProperties(fname=r"c:\windows\fonts\方正粗倩简体.ttf", size=12)
titleYW_font_set = FontProperties(fname=r"c:\windows\fonts\Gabriola.ttf", size=20)
titleZW_font_set = FontProperties(fname=r"c:\windows\fonts\汉仪细行楷简.ttf", size=18)
# rvs: Random Variates
# pdf: Probability Density Function 概率密度函数
# cdf: Cumulative Distribution Function 概率密度函数的积分函数
# sf: Survival Function (1-CDF)
# ppf: Percent Point Function (Inverse of CDF) 百分点函数,概率密度函数的积分值
# isf: Inverse Survival Function (Inverse of SF)
# stats: Return mean, variance, (Fisher’s) skew, or (Fisher’s) kurtosis
# moment: non-central moments of the distribution
# ppf以概率的形式,查询函数值-----------类似分布临界表
plt.figure()
# example ------------------------------------------- 卡方分布(右侧单边)
plt.subplot2grid((2, 2), (0, 0))
df = 20 # 自由度
# print(chi2.ppf(0.01, df)) # 计算函q=0.01概率时数值。其中 q = 1-a
# print(chi2.cdf(8.260, df)) # 知道x值求a
x = np.linspace(chi2.ppf(0.01, df), # 绘制概率密度图
chi2.ppf(0.99, df), 100)
plt.plot(x, chi2.pdf(x, df), alpha=0.6, label='chi2 pdf')
plt.title(u'自由度为20时的卡方概率密度函数图', fontproperties=titleZW_font_set, size=10)
# 计算平均数、方差、标准差
# print(chi2.mean(df))
# print(chi2.var(df))
# print(chi2.std(df))
# example ---------------------------------------------------- 标准正态分布(左侧单边)
plt.subplot2grid((2, 2), (0, 1))
# print(norm.ppf(0.6179)) # 知道q时求x, q=a
# print(norm.cdf(0.3)) # 知道x时求q
x = np.linspace(norm.ppf(0.01), norm.ppf(0.99), 100)
plt.plot(x, norm.pdf(x), alpha=0.6, label='norm pdf')
plt.title(u'标准正态分布概率密度函数图', fontproperties=titleZW_font_set, size=10)
# example ----------------------------------------------------- t分布(双边分布)
plt.subplot2grid((2, 2), (1, 0))
df = 15
x = np.linspace(t.ppf(0.01, df), t.ppf(0.99, df), 100)
# print(t.ppf(0.95, df)) # q=0.95,a=(1-q)*2
# print(t.cdf(1.753, df))
plt.plot(x, t.pdf(x, df), alpha=0.6, label='t pdf')
plt.title(u'自由度为15时的t分布概率密度函数图', fontproperties=titleZW_font_set, size=10)
# example ------------------------------------------------------ F分布(右侧单边分布)
plt.subplot2grid((2, 2), (1, 1))
df = 5
dn = 8
x = np.linspace(f.ppf(0.01, df, dn), f.ppf(0.99, df, dn), 100)
# print(f.ppf(0.95, df, dn))
plt.plot(x, f.pdf(x, df, dn), alpha=0.6, label='f pdf')
plt.title(u'自由度为5和8时的f分布概率密度函数图', fontproperties=titleZW_font_set, size=10)
# example ------------------------------------------------------- 非标准正态分布
plt.figure()
std = 1
mean = 2
normalDistribution = stats.norm(mean, std) # 构建统计分布
x = np.linspace(normalDistribution.ppf(0.01), normalDistribution.ppf(0.99), 100)
plt.plot(x, normalDistribution.pdf(x))
# plt.show()
# example -------------------------------------------------------- 对连续数据进行正态拟合
plt.figure()
train = pd.read_csv("csv/Titanic/train.csv")
train_Age = train.dropna(subset=['Age'])
M_S = stats.norm.fit(train_Age['Age']) # 正态拟合的平均值与标准差
train_Age['Age'].plot(kind='kde') # 原本的概率密度分布图
normalDistribution = stats.norm(M_S[0], M_S[1]) # 绘制拟合的正态分布图
x = np.linspace(normalDistribution.ppf(0.01), normalDistribution.ppf(0.99), 100)
plt.plot(x, normalDistribution.pdf(x), c='orange')
plt.xlabel('Age about Titanic')
plt.title('Titanic[Age] on NormalDistribution', size=20)
plt.legend(['Origin', 'NormDistribution'])
np.random.normal()的意思是一个正态分布,normal这里是正态的意思。
numpy.random.normal(loc=0,scale=1e-2,size=shape)
参数loc(float):正态分布的均值,对应着这个分布的中心。
参数scale(float):正态分布的标准差
参数size(int 或者整数元组):输出矩阵的shape,默认为None。
# ----------------------------------------------------------------- R x C列联表,独立性检验
# 建立关于性别与存活
train_pclass_0 = train['Pclass'][train['Survived'] == 0].value_counts()
train_pclass_1 = train['Pclass'][train['Survived'] == 1].value_counts()
train_pclass_01 = pd.concat([train_pclass_0, train_pclass_1], axis=1, sort=True)
train_pclass_01.columns = ['Not_Survived', 'Survived']
g, p, dof, expctd = chi2_contingency(train_pclass_01.values) # g为chi2值,服从自由度为dof的卡方分布
print(g)
# 拟合优度检验,判断两个分类型变量是否独立
# 首先绘制卡方自由度为dof的曲线
plt.figure()
x = np.linspace(chi2.ppf(0.01, dof), chi2.ppf(0.99, dof), 100)
plt.plot(x, chi2.pdf(x, dof))
# 以95%置信区间,查看小概率事件区间
plt.axvline(chi2.ppf(0.975, dof), color='r')
plt.axvline(chi2.ppf(0.025, dof), color='r')
plt.title('chi2 distribution'+'whose dof is '+str(dof))
plt.text(chi2.ppf(0.975, dof), 0.02, 'q=0.95,z='+str(round(chi2.ppf(0.975, dof), 2)), ha='right', va='top', color='g', alpha=0.8, size=15)
plt.text(chi2.ppf(0.025, dof), 0.02, 'q=0.05,z='+str(round(chi2.ppf(0.025, dof), 2)), ha='left', va='top', color='g', alpha=0.8, size=15)
plt.show()






















