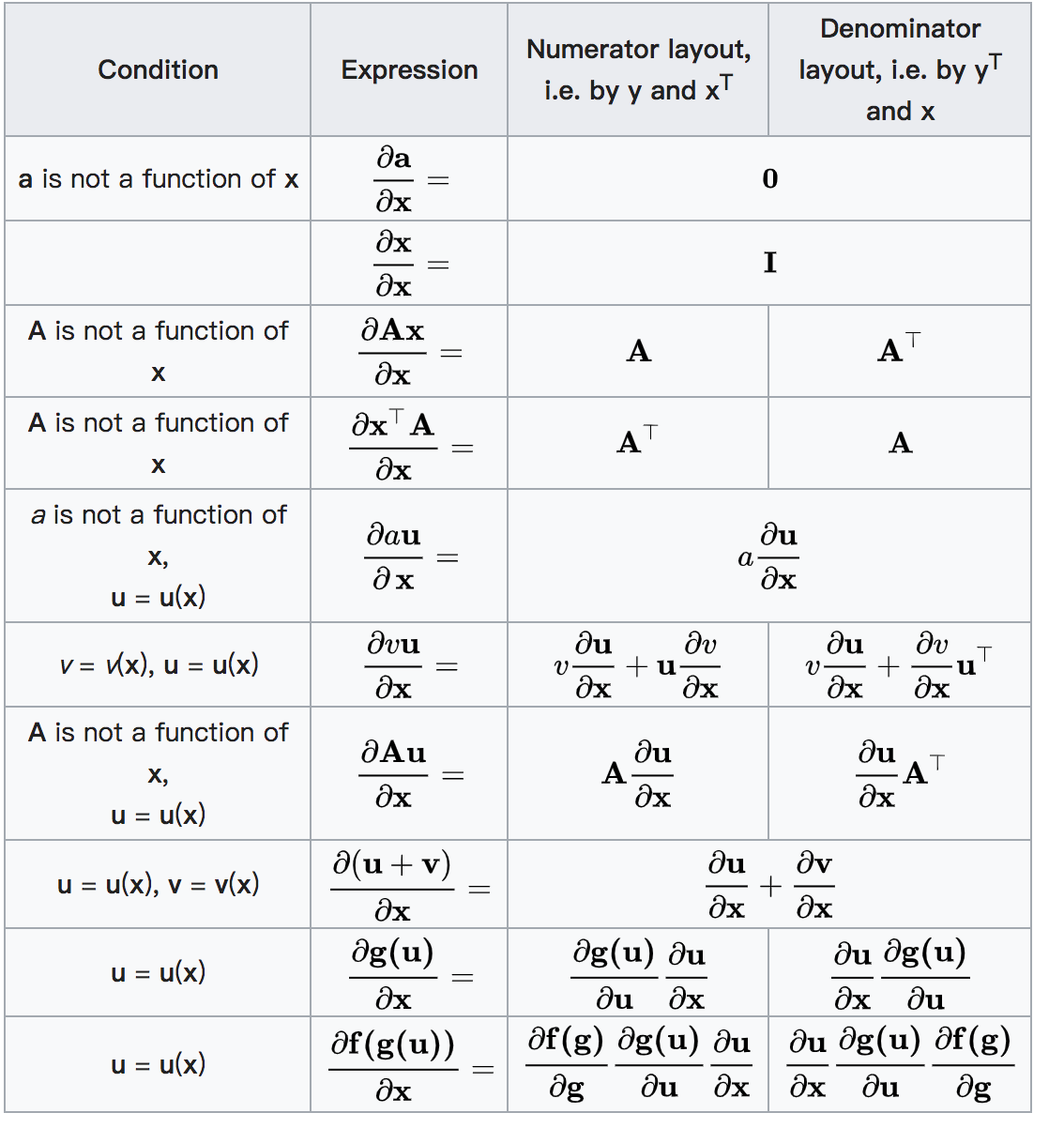
本文让大家更好地学习使用向量、矩阵和高阶张量的求导。1 简化,简化再简化很多关于数组的求导的困惑来自于一次性想做太多事。这些事包括同时对多个部分求导,和式的求导,和应用链式法则。同时做这么多事情,至少在我们还没有足够熟练之前,那就很容易会出现错误。1.1 对每个部分展开式子成显式求和及等式为了简化一个给定的计算,通常将对于输出的一个简单的标量元素使用标量变量展开成显式公式。一旦我们对于输出的单个标
转载
2024-03-06 18:00:38
15阅读
目录1、f'(x)=lim(h->0)[(f(x+h)-f(x))/h]2、f(x)=a的导数, f'(x)=0, a为常数3、f(x)=x^n的导数, f'(x)=nx^(n-1), n为正整数4、f(x)=x^a的导数, f'(x)=ax^(a-1), a为实数5、f(x)=a^x的导数, f'(x)=a^xlna, a>0且a不等于16、f(x)=e^x的导数, f'(x)=e^
转载
2023-07-28 14:24:31
991阅读

 ...
转载
2021-09-16 10:33:00
430阅读
2评论
设计函数求一元多项式的导数。(注:xn(n为整数)的一阶导数为nxn−1。)输入格式: 以指数递降方式输入多项式非零项系数和指数(绝对值均为不超过 1000 的整数)。数字间以空格分隔。输出格式: 以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。注意“零多项式”的指数和系数都是 0,但是表示为 0 0。(这句话的意思其实是 0 的n次方求导后对应的输出为
转载
2023-08-21 14:59:28
259阅读
1第一次作业1.1题目描述 对形如4*x+x^2+x的多项式求导。1.2类图1.3度量分析 在完成第一次作业时,我的写法没有特别的“面向对象”。唯一封装起来的是Node,代表多项式的一个项。PolyDerivation是一个方法庞杂的类,先判断输入是否合法,再将多项式拆分成独立的项,接着求导,同时也包含了程序的入口main。这无疑是一个面向方法的写法。 写valid方法判断合法性的时候,经历
转载
2023-07-17 23:53:26
114阅读

原创
2022-06-18 00:26:03
679阅读

2019年北航OO第1单元(表达式求导)总结1 基于度量的程序结构分析量化指标及分析以下是三次作业的量化指标统计:关于图中指标在这里简要介绍一下:ev(G):基本复杂度,用来衡量程序非结构化程度。基本复杂度高意味着非结构化程度高,难以模块化和维护。Iv(G):模块设计复杂度,用来衡量模块判定结构,即模块和其他模块的调用关系。模块设计复杂度高意味模块耦合度高,这将导致模块难于隔离、维护和复用。v(G
转载
2023-12-28 23:13:07
27阅读

前言在前三次OO作业中,我们重点对程序的输入输出设计、程序结构与层次化设计、程序鲁棒性进行了学习与应用,实现了由易到难的表达式求导程序。对于之前一直习惯于面向过程编程的我而言,这三次作业着实是一个不小的挑战。由于对于程序结构性设计的考虑欠妥,导致每次作业的拓展性较差,越往后走越能发现程序出现bug的机率上升,而且bug的查找与修复过于依赖测试点,修复过程中也存在按下葫芦浮起瓢的情况。借助这一次博客
转载
2023-11-06 15:18:31
45阅读

最近点对问题:给定平面上的N个点,找出距离最近的两个点。分治法:
1 )如果数组长度(即点的个数,一般≤3)在一定范围内时直接求出最近点,蛮力求解,递归退出条件;
&nb
转载
2024-01-14 17:49:03
47阅读
上一篇文章我们复习了函数求导的定义和一些常见函数的导数,今天这篇文章我们回顾一下复杂函数的求导方法。先强调一下,今天的文章很重要,想要看懂机器学习各种公式推导,想要能够自己推一推各种公式,函数求导是基础中的基础,在算法这个领域,它比积分要重要得多。我们先来看第一种情况:多个函数进行四则运算的导数。函数四则运算求导法则我们假设和都在x点有导数,那么它们进行加减乘除四则运算之后的结果的导数有如下性质:
原创
2021-04-29 16:29:11
1405阅读
Strange fuction Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 4717 Accepted Submission(s): 3383
原创
2023-04-20 11:34:24
61阅读
# Java求导教程
## 1. 整体流程
在解决问题之前,我们首先要了解整个求导的流程。下面是求导的基本步骤表格:
| 步骤 | 描述 |
| --- | --- |
| 步骤1 | 输入被求导函数 |
| 步骤2 | 将函数转化为可求导的形式 |
| 步骤3 | 使用求导规则进行求导 |
| 步骤4 | 输出求导结果 |
现在我们将逐一介绍每个步骤需要做的事情。
## 2. 步骤详解
原创
2023-09-03 06:04:16
258阅读
OO_JAVA_表达式求导_第一弹---------------------------------------------------表达式提取部分词法分析 首先,每一个表达式内部都存在不可分割的字符组,比如一个不止一位的数字,或是一个sin三角函数,这样不能分离的字符组我称之为词法单元,依照其定义,可以将第三次作业的表达式分割成如下词法单元:SPACE:即空格和TAB字符的组合纯数字:即纯粹由
转载
2023-11-06 13:34:10
159阅读

和、差、积、商求导法则 设u=u(x),v=v(x)都可导,则:(Cu)’ = Cu’, C是常数 (u ± v)’ = u’ ± v’ (uv)’ = u’v + uv’ (u/v)’ = (u’v – uv’) / v2 1、2不解释,下面给出3、4的推导过程乘法法则的推导过程 乘法法则可扩展:除法法则的推导过程示例1:f'(1/x)...
原创
2021-06-07 16:58:57
5229阅读
和、差、积、商求导法则 设u=u(x),v=v(x)都可导,则:(Cu)’ = Cu’, C是常数 (u ± v)’ = u’ ± v’ (uv)’ = u’v + uv’ (u/v)’ = (u’v – uv’) / v2 1、2不解释,下面给出3、4的推导过程乘法法则的推导过程 乘法法则可扩展:除法法则的推导过程示例1:f'(1/x)...
原创
2022-01-16 18:20:15
6799阅读
## JAVA 求导函数
### 1. 引言
在数学领域中,求导函数是一种非常重要的概念。它用来描述函数在某一点的变化率,可以帮助我们研究函数的性质和解决实际问题。在计算机科学中,通过使用编程语言,我们可以实现求导函数的功能。本文将介绍如何在Java中实现求导函数,并提供相应的代码示例。
### 2. 求导函数的定义
求导函数的定义可以通过极限的概念来描述。对于一个函数f(x),它在某点x
原创
2023-11-15 05:20:16
225阅读
# 在 Java 中实现求导数
求导数是微积分中的重要概念,尤其在科学与工程领域应用广泛。在这篇文章中,我们将学习如何在 Java 中实现一个简单的求导数工具。我们会分步进行,通过使用表格、流程图和序列图来帮助理解整个过程。
## 1. 整体流程
首先,了解求导数的整体流程。我们可以将其划分为以下几个步骤:
| 步骤 | 描述 |
|------|------|
| 1 | 定义一个
# Java 向量求导:基础与实践
在机器学习和数据科学领域,向量的求导是一个重要的工具,它帮助我们优化模型和计算梯度。在Java中,通过使用标准数学库和自定义方法,我们可以实现向量的求导功能。本文将深入解析向量求导的基本概念,并提供Java代码示例,以便您更好地理解这一主题。
## 什么是向量求导?
在数学上,**向量**是一个有大小和方向的量。在多变量函数中,求导过程涉及到对每个变量的偏
原创
2024-09-06 05:49:17
14阅读
# Java求导函数
在数学中,求导是一个重要的概念。它可以帮助我们判断函数在某一点的斜率和变化趋势。在计算机编程领域,我们也可以使用Java来实现求导函数。本文将介绍什么是求导,为什么需要求导,以及如何使用Java来实现求导函数。
## 什么是求导?
求导是微积分的一个基本概念,它用于计算函数在某一点的斜率。在数学中,函数的导数是函数在某一点处的斜率,它表示了函数在该点的变化趋势。求导可以
原创
2023-08-17 15:40:30
297阅读
# Java 求导数:基础概念与实现
导数是微积分中的一个基本概念,它用于衡量一个函数在某一点的变化率。在编程中,尤其是使用Java语言时,我们如何实现求导操作呢?本文将给出一个简单的示例,讲解如何在Java中实现自动求导。
## 一、求导的基本概念
求导的基本思想是计算函数在某一点的斜率。简单来说,给定一个函数 \(f(x)\),它的导数表示为 \(f'(x)\),可以通过以下极限公式定义
原创
2024-08-16 09:31:18
88阅读



