UVa 1193 / POJ 1328 / Beijing 2002 Radar Installation (贪心&区间选点)

1193 - Radar Installation

Time limit: 3.000 seconds

http://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=3634

http://poj.org/problem?id=1328

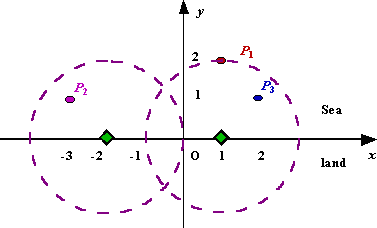
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d

We use Cartesian coordinate system, defining the coasting is the x -axis. The sea side is above x -axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x -y

Input

The input consists of several test cases. The first line of each case contains two integers n (1n1000)and d , where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n

The input is terminated by a line containing pair of zeros.

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. `-1' installation means no solution for that case.

Sample Input

3 21 2 -3 1 2 1 1 2 0 2 0 0

Sample Output

Case 1: 2Case 2: 1

对于每个小岛，对应着x轴上的一段区间，我们就是要用最少的点，让每个区间内都至少有一个点。

当然也可以对x排序（区间中点）

完整代码：

/*UVa: 0.018s*/
/*POJ: 16ms,188KB*/

#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

struct node
{
	int x, y;
	bool operator < (const node a) const
	{
		return x < a.x;
	}
} island[1000];

int main(void)
{
	int n, i, count, cid = 0;
	double tx, lx, rx, llx, rrx, d;
	while (scanf("%d%lf", &n, &d), n)
	{
		for (i = 0; i < n; i++)
			scanf("%d%d", &island[i].x, &island[i].y);
		sort(island, island + n);
		count = 0;
		for (i = 0; i < n; i++)
		{
			if (island[i].y > d || island[i].y < 0)
			{
				count = -1;
				break;
			}
			if (i == 0)
			{
				count = 1;
				tx = sqrt(d * d - island[i].y * island[i].y);
				lx = island[i].x - tx;
				rx = island[i].x + tx;
			}
			else
			{
				tx = sqrt(d * d - island[i].y * island[i].y);
				llx = island[i].x - tx;
				rrx = island[i].x + tx;
				if (llx <= rx && rrx >= lx)
				{
					lx = (lx < llx) ? llx : lx;
					rx = (rx > rrx) ? rrx : rx;
				}
				else
				{
					count++;
					lx = llx;
					rx = rrx;
				}
			}
		}
		printf("Case %d: %d\n", ++cid, count);
	}
}