首先还是一样,让我们看看什么是素数。素数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
因此我们从简单的开始,例:找出100->200之间的所有素数。
同样我们需要
- 遍历100->200的所有自然数,这次我们使用for循环来实现遍历。
- 判断是否因数只有1和其本身,我们只要循环判断该数在1到它本身没有其他因数即可
- 我们看到使用了两次循环,因此我们应该循环嵌套
- 当然为了直观看出代码的效率我们使用count来计数(count1为运行次数,count2为有效次数)
由此我们写出如下代码:
#include<stdio.h>
int main ()
{
int i = 0,count1,count2; //count计数器
for(i=100;i<=200;i++) //i的遍历
{
int j;
for(j=2;j<=i;j++) //因子j
{
count1++; //内循环一次计一次
if(i%j == 0) //若整除我们则确定为不是素数
{
break; //直接break跳出减少次数
}
}
if(i == j) //若j到i时还没整除则为素数,打印i,计为一次有效
{
printf("%d\t",i);
count2++;
}
}
printf("\n");
printf("一共运行了%d次\n",count1);
printf("一共有素数%d个\n",count2);
return 0;
}运行结果如下:
101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
一共运行了3314次
一共有素数21个
--------------------------------
Process exited after 0.09238 seconds with return value 0
请按任意键继续. . .我们看到这个效率并不是很高,那是否可以优化一下算法呢?
我们思考知道偶数一定不是素数因此得出:
#include<stdio.h>
int main ()
{
int i = 0,count1,count2;
for(i=101;i<=200;i+=2) //我们这里改变i从首个奇数101开始,每次循环+2,跳过偶数判断
{
int j;
for(j=2;j<=i;j++)
{
count1++;
if(i%j == 0)
{
break;
}
}
if(i == j)
{
printf("%d\t",i);
count2++;
}
}
printf("\n");
printf("一共运行了%d次\n",count1);
printf("一共有素数%d个\n",count2);
return 0;
}结果如下:
101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
一共运行了3263次
一共有素数21个
--------------------------------
Process exited after 0.06562 seconds with return value 0
请按任意键继续. . .我们看到结果一样,但运行次数确实减少了,达到了优化的目的。
但这个优化是否还可以近一步?
我们知道一个合数一定可以写成两个数的积(即:i=a*b),由此知道a,b中一定有一个数小于根号i,
另一个大于根号i。
所有我们判断i是否为素数,只需要判断i在根号i范围内没有因子即可
我们在代码中引入数学库函数,代码如下:
#include<stdio.h>
#include<math.h>
int main ()
{
int i = 0,count1,count2;
for(i=101;i<=200;i+=2)
{
int j;
for(j=2;j<=sqrt(i);j++) //循环范围改变
{
count1++;
if(i%j == 0)
{
break;
}
}
if(j>sqrt(i)) //判断条件改变
{
printf("%d\t",i);
count2++;
}
}
printf("\n");
printf("一共运行了%d次\n",count1);
printf("一共有素数%d个\n",count2);
return 0;
}运行结果如下:
101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
一共运行了367次
一共有素数21个
--------------------------------
Process exited after 0.08626 seconds with return value 0
请按任意键继续. . .同样,素数个数一样,但运行极大的减少了。
如果我们要从1到20000范围查找素数,比较三种方法的效率高低,得出
一个有2262个素数
方法1:一共运行了21269832次
方法2:一共运行了21259833次
方法3:一共运行了291302次
确实可以看出方法3的效率
以上方法我们通常叫做试除法(一个一个除再判断)
接下来我们还有筛选法
筛选法也叫埃氏筛选法
筛选法和试除法其实有着本质上的区别,试除法是判断每个数是不是素数来达到目的;而筛选法不是,筛选法是将不是素数的数全部去除,然后得到余下的数来达到目的。
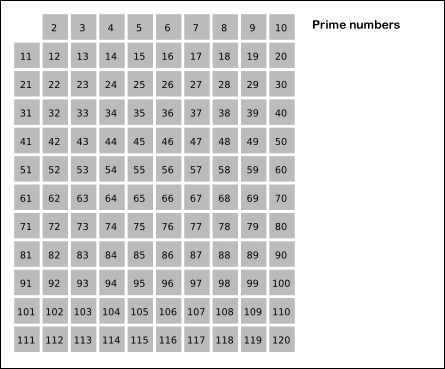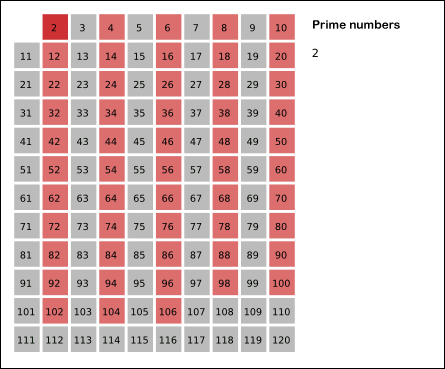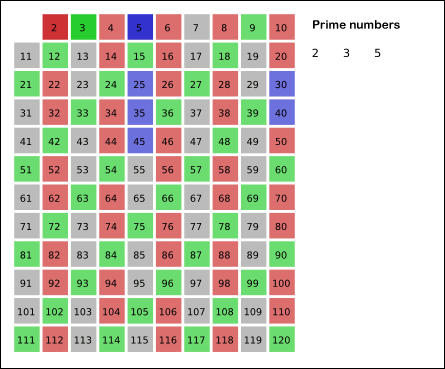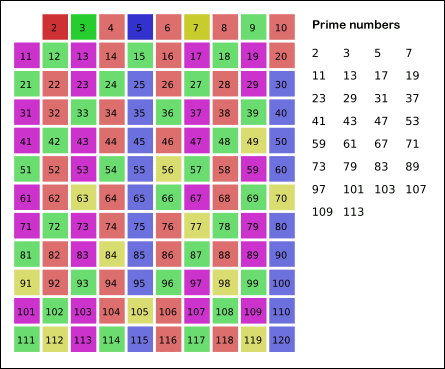
首先1不是质数也不是合数,所以要划去;接着2是公认最小的质数,所以要保留下来,再把所有2的倍数去掉;然后接下来遇到的第一数不会是2的倍数,所以它必然只可能被1和他自身整除,为素数,而2后面第一个没有被划去的数是3,所以要保留素数3,再把所有3的倍数去掉;接着往复之前的判断,剩下的那些大于3的数里面,最小的是5,所以5也是质数,再去掉五的倍数......
上述过程不断重复,就可以把某个范围内的合数全都除去(就像被筛子筛掉一样),剩下的就是质数了。如果理解还不怎么清晰,来看看直观地体现出筛法的工作图,如下所示:
下面我们来看看如何实现。
看图我们发现
- 它先找到一个最小的素数,再其排除所有的倍数(这里我们使用for循环排除)
- 然后我们思考如何才能使排除的数不再循环判断(这里我们可以用判断语句,使排除的数不符合条件,从而达到不循环的目的)
- if判断条件有0为假的特点,所以我们想到给所有的被排除数赋值为0,这里使用数组即可
我们还是以100->200为例再原有代码的基础上更改
从而有如下代码:
#include<stdio.h>
int main()
{
int i=0,count1=0,count2=0,arr[201] = {0};
for(i=2;i<=200;i++) //给数组赋初始值
arr[i]=1; //这里初值不为0即可,使开始所有数符合循环条件
for(i=2;i<=200;i++)
{
if(arr[i]) //这里注意,因为第一次是2进来,且后面排除的数不会进来
{ //因此能进来的一定是素数
int j=0;
if(i>=100 && i<=200) //这里判断100->200之间,然后下面打印
{
printf("%d\t",i);
count2++; //计素数
}
for(j=i+i;j<=200;j+=i) //开始排除倍数
{
arr[j] = 0; //使被排除的数不符合判断条件
count1++; //分析出排除次数等于运行次数
}
}
}
printf("\n");
printf("一共运行了%d次\n",count1);
printf("一共有素数%d个\n",count2);
return 0;
}运行结果如下:
101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
一共运行了323次
一共有素数21个
--------------------------------
Process exited after 0.05069 seconds with return value 0
请按任意键继续. . .运行结果看出,运行效率确实更好了,数据越多效果越明显。
我们分析运行过程,发现还可以更优化,例如:6=2*3;这里的2我们排除了一次后3又排除了一次,
相当于6排查了两次,还可以优化一下,使每个数只排查一遍
即:我们排查2时从2*2开始排查,排查3时从3*3开始排查,而2*3在排查2时已经查过了;同理排查4时从4*4开始,2*4和3*4在2和3时查过,如此我们每次只需要从i*i开始排查即可
于是得到代码如下:
#include<stdio.h>
int main()
{
int i=0,count1=0,count2=0,arr[201] = {0};
for(i=2;i<=200;i++)
arr[i]=1;
for(i=2;i<=200;i++)
{
if(arr[i])
{
int j=0;
if(i>=100 && i<=200)
{
printf("%d\t",i);
count2++;
}
for(j=i*i;j<=200;j+=i) //从i*i开始
{
arr[j] = 0;
count1++;
}
}
}
printf("\n");
printf("一共运行了%d次\n",count1);
printf("一共有素数%d个\n",count2);
return 0;
}运行结果:
101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199
一共运行了232次
一共有素数21个
--------------------------------
Process exited after 0.05693 seconds with return value 0
请按任意键继续. . .然后我们来查小于20000的素数,比较几种方法的效率;
方法4:一共运行了47864次
方法5:一共运行了35485次
看出来了吗,筛选法只用了几万次,而试除法运行了几十万次,甚至几千万次
在庞大的基数下筛选法的效率就体现出来了。
然而我们还会发现16=4*4=2*8,我们还是有一些数据排查过两次,类似的完全平方数例如36,64等
我们是否还能再优化呢?找到这些数和代码之间的微妙联系,试着分析可行性吧。























