embedding用与数据降维 数据降维的目的

前几个章节我们将了机器学习的基础知识以及数据预处理和特征选择，本章节我们将讲述数据降维，在次之前，首先我们要明白为什么要进行数据降维操作？

• 加快运算速度
• 有利于防止过拟合（但防止过拟合最好的方法却是正则化）
• 减少用来存储数据的空间

2.3数据降维

当特征选择完成之后，可以直接训练模型，但是可能由于矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也就必不可少了。数据降维可以保证原始数据信息量没有缩减的条件下减少特征量。

• 维度越高，数据的每个特征维度上的分布就越是稀疏，这对机器学习算法基本上是灾难性的，我们称之为维灾难。
• 特征有比较明显的自相关性时会让很多模型的效果变差，因此先降维。
• 有些时候降维没多大关系，纯粹时为了去除杂质;
• PCA没有类别信息的，不知道样本属于哪个类，通过用PCA对全体数据进行操作；LDA有类别信息，将会投影到类间距最小和类间距最大的特征间;

通常情况下，我们会使用PCA和LDA两种方式进行降维，但是他们的应用场景和原理也都是不一样的。PCA是选择投影后使得数据方差最大的方向进行投影，方差越大信息量越多，而且PCA是无监督算法，没有类别之分。如果我们的目的是分类，那么毫无疑问LDA更加合理，LDA是无监督的，LDA投影后使得类内方差小而类间方差变大，用到了类别信息。

2.3.1主成分分析(PCA)

找到数据方差最大的方向。降维之后的数据可以代表原来数据的所有特征，但是这些数据却失去了实际的意义。

算法流程：

• 数据预处理：中心化
• 求样本的协方差矩阵;
• 对协方差矩阵做特征值分解
• 选出最大的k个特征值对应的k个特征向量
• 将原始数据投影到选取的特征向量上；
• 输出投影后的数据集；

方差指的是一个向量数据内部的离散程度；而协方差描述的是两个向量数据之间的相关性

协方差只能处理两维的数据，当维度多了之后就需要多个协方差，这个时候就需要我们通过矩阵来组织这些数据，协方差矩阵就是一个对称的矩阵，对角线是各个维度的方差。

下面我们举个例子：

m个样本为n个特征的数据。也就是m*n的矩阵，这时候我们让该矩阵与其转置矩阵相乘就得到了协方差矩阵。

 

 

2.3.2线性判别分析(LDA)

2.3.2.1简单介绍

该方法在NLP中被称为是文档主题模型。既可以用于分类,也可以用来降维.通过投影的方式投影到维度更低的空间中，使得投影后的点按照类别区分，同一类别的数据点在投影后的空间中更加接近。使得类内方差最小类间方差最大(最大化类间距离最小化类内距离)。

2.3.2.2公式推导

目的：类间的方差最大，类内的方差最小。eg：

首先定义两个样本C1和C2，均值分别为u1，u2，投影方向为w，那么投影之后两个样本之间的距离(两个簇中心点之间的距离)表示为：

接着表示出投影后样本的方差

构建优化目标

化简之后可以得到

此时我们分别定义类间散度矩阵Sb和类内散度矩阵Sw：

优化目标简化为：

我们认为最大化的J(w)就是

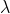
，这时可得：

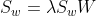
整理之后可得：

总之，我们最大化目标值就是选出对应矩阵最大的特征之

。

2.3.2.3LDA流程

1. 计算每个类别的均值ui和全局样本的均值u
2. 计算类内散度矩阵Sw和类间散度矩阵Sb，以及全局散度矩阵St
3. 对矩阵做特征值分解;
4. 取出最大的d’个特征值作为对应的特征向量
5. 计算投影矩阵；