为什么会出现CORDIC算法呢?
对于三角函数计算,理论接触较多的应该就是级数展开的方法 ,通过逼近的方式进行计算,比如泰勒级数。但是因为这种多项式函数在计算的过程中需要大量使用到浮点数计算,而对于缺乏硬件乘法器的器件而言这种计算方式的实现是很困难的。有了问题,自然就会有人出来解决,1959年J. Volder就首次提出了CORDIC算法,只需要进行移位和加减运算的快速算法。
CORDIC算法能干什么?
这里只介绍关于三角函数方面CORDIC的作用:
1、得到坐标轴上一点的角度(相位信息);
2、得到坐标轴上一点对应的cos(a)和sin(a) (幅值信息)。
ps:使用cordic计算幅值的方法不好,可以选择更好的,比如查找表的方法,因此这里不再过多介绍计算幅值的方法。
CORDIC算法的原理是什么?
对于坐标轴上点的相位,就是和x轴正半轴(后面统称x轴)的夹角。求一个点的相位也就是将要求的点进行旋转,当点旋转到与x轴第一次重合时,旋转过的相位大小就是这个点的相位。CORDIC算法通俗来讲就是把这个旋转过程变成了“离散”旋转,每次旋转特定的角度,旋转N次。在旋转过程中不停的判断,如果落在x轴就停止,如果发现在x轴上方就逆时针旋转(相位增加),如果发现在x轴下方就顺时针旋转(相位减小),将旋转过程中的相位变化进行累加,最终就可以得到一个点的相位。这里可以总结这个旋转过程有两点要求:
1、旋转过程中能够实时得到y的值,因为我们需要y的值来判断我们旋转的点是否到达了x轴(点在第一象限的话,y=0则表明点落在了x轴上);
2、每次旋转需要知道旋转的角度,以便于计算相位。
有了上面的原理,现在需要做的就是得到一个点在坐标轴上旋转和相位的关系式。
首先假设坐标轴上有任意一点(x0,y0)经过旋转后得到(x1,y1),如下图所示:

因为是旋转,幅值相等,则可以推导公式:

ps:这里介绍一种方便的方法推导,使用复变函数推导相位旋转,有兴趣化简一下即可对应上面的公式:

这里可以把(x0,y0)看作是输入点,上面的公式的确满足了旋转的第一个要求,也就是可以实时计算出旋转后的y值,但是这个公式中包含了
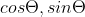
,它们计算起来已经很复杂了,怎么办呢?接下来就是取巧的过程:
1、对于cosΘ而言,只是影响y值的大小,但是并不影响判断点是否落在x轴上,因此这里直接将cosΘ省略;
2、对于任意的tanΘ的确不好求其结果,但是我们可以限制每次旋转的角度,使tanΘ的值是特殊值,这里选择的tanΘ值是(1,1/2,1/4,...,1/(2^n))。这里值的选择是方便硬件进行计算,可以直接进行算术右移,最大限度简化操作。
3、既然tanΘ的值有了,那么对于每次旋转的角度Θ值而言也就是确定的了(45,26.565051177078,14.0362434679265等等)。对于实际工程而言,旋转次数(迭代)肯定是有限的,这个次数是和浮点数转化为定点数精度有关的。比如转化精度是浮点数1转化为定点数256,则45°对应的定点数是45*256=11520,且能分辨的最小Θ值是1/256=0.00390625°。因为有最小分辨率限制,如果角度再小也就没有意义了,因此如果转化倍数是256,则最大迭代次数是15次。
ps:CORDIC算法只是一个近似计算,也就是说15次迭代后点不一定是落在x轴上的。转化精度也高,迭代次数越多,结果越准确
有了上面的推论,相位旋转公式可以写成:

对于旋转过程中相位累加的公式可以写成:

这里的z是有初始值的,初始值和象限有关,第一象限和第四就是z=0(x>0),第二象限就是z=90(y>0),第三象限就是z=-90(y<0)。在下面给出的示例代码中,是默认输入值x>0的。如果想将程序扩展到四个象限,判断输入点的象限,然后取z的不同初始值和对输入点进行象限变换(比如输入点在第二象限(x0,y0),则将点逆时针旋转90°得到新点(y0,-x0))即可,有兴趣的可以进行添加





















