
前言:
本章的目的是弄清楚法线的数学基础,让我们一齐撬开光照系统的大门吧!
正文:
首先从2维的角度来看,我们在直角坐标系中随便点两个点,无论我们点在哪里,这两个点都会有共线(colinear)的性质,也就是必定有一条直线可以穿过它们。

12.1 无论连点在哪里,都必定有一条直线可以穿过它们
除此之外,还有一条直线可以垂直地穿过这两个点所定义的线,使得两线之间呈90度垂直。这条线就是法线。
![a06485eb8e95b6305ec2d1970f70e93d.png blender 光滑组_unity shader [gamma]_03](https://s2.51cto.com/images/blog/202410/04234121_67000ca1460db65787.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
12.2 两线垂直相交
当我们谈到法线(Normal),即标准化(Normalized)的向量(Vector)时,其实说的是一个单位长度(Unit Length)的向量,它的长度满足如下公式:

对向量计算感兴趣的读者可以参阅下面这篇文章。文章的作者用JS实现了一个简单的向量标准化模型,玩着还挺有趣,请务必拜读。
https://www.khanacademy.org/computing/computer-programming/programming-natural-simulations/programming-vectors/a/vector-magnitude-normalizationwww.khanacademy.org
每一条直线都存在着两个可计算的标准化向量,一个向上一个向下。

12.3 两个相反方向的标准化向量垂直于直线
这里的向量可以用来做很多东西,除了反射等光照计算外,物理计算也是一大主要用途。比如一个球以给定波动角度(Incident Angle)弹到与直线平行的平面上时,会以何种角度反弹回去。

12.4 物体以相同的波动角度弹入及弹出平面(不考虑阻力及能量损耗)
除此之外,还有类似“角色沿着直线向下滑行时会以何种速度移动?”这种问题,也可以通过计算法线来得到解答。
关于Normal在二维空间的表示大概就是这样了,那么3D的世界里是怎么样的呢?
同样,随便画两个点就可以产生一条有共线特性的直线,那么随便画3个点则可以产生一个有共面

12.5 共面指的是这三个点必定会出现在同一个平面上
然而4个或以上的点则不一定会产生共面,这是因为第四个点只要朝着平面法线的方向移动,就必定会偏离平面。读者可以去这里观察由不同数量的点组成的几何模型。
Definition of Coplanarwww.mathsisfun.com
关于共面的几何含义就不多讲了,为了方便之后的讲解,下面的3维模型统一使用四边形来说明。
一个平面上也存在两个不同方向的标准化向量,如图所示:
![330342f2955c62323f727aef2d88de31.png blender 光滑组_unity shader [gamma]_08](https://s2.51cto.com/images/blog/202410/04234122_67000ca2508b529995.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
12.6
这两个法向量同样是指向相反方向,我们可以说它们是这个平面的正交线(Orthogonal line),因为它们在透视系统中与平面呈90度直角正交叉。
为了得到法线的标准化向量,我们需要对多变形的其中两条线进行叉乘,并获得标准化的结果。与点乘不同,叉乘的结果是一个向量而不是一个标量,因此我们需要用到的这两条线其实也是一个向量,为了得到向量的积,我们需要从某个点出发,然后获取其指向另外两个点的方向,并将两个向量进行叉乘,最终得出的叉积与两个向量和垂直,也就是我们需要的法线向量。

12.7
关于叉乘的更多资讯,可以拜读牧野的文章:
blog.csdn.net
但是实际上我们很少需要亲自使用叉乘来计算法线向量。(那你之前说那么多干嘛)通常我们导入模型的时候,它就已经拥有法线了,如果没有那我们就打爆美术的狗头(删掉)。
我们已经看过了一点法线的数学基础,因此通常刚入门的同学都会理所当然地认为法线就是一个面正方向只有一个标准法线,但其实在各大3D建模软件里面,法线是逐个顶点提供的。以上面的正方形为例,建模软件为其计算4个对应顶点的法线。

12.8 以Blender为例,模型上面的四边形拥有4个正法线向量
为什么是这样做呢?由于模型的四边形动不动便是成千上百,因此法线的计算本身也是非常损耗资源的,因此如此一来的话相邻四边形之间便可以有一些法线是共享的(面之间有些顶点也是共享的,建过模的都懂)
那么既然模型自带法线,那就好办了,在Unity中法线应该是和顶点信息一样,可以通过语义获取。在编写appdata与v2f结构体时,加入一个NORMAL属性
float3 normal : NORMAL;
自问自答
为什么Vertex位置信息是一个float4类型,而法线是float3类型,不都是点嘛?
顶点坐标和正切线是float4,表示齐次坐标,用于投影几何。我们一般见到的3维坐标其实是欧氏几何里的笛卡儿坐标。而齐次坐标则是在此之上加上了一个w坐标轴,用以表示这个点是一个向量还是点。
那么接下来看一段简单的shader:
v2f vert(appdata v)
{
v2f o;
o.vertex = mul(UNITY_MATRIX_MVP, v.vertex);
o.normal = normalize(v.normal);
return o;
}
float4 frag(v2f i) : SV_Target
{
float3 color = (i.normal + 1) *0.5;
return float4(color.rgb, 1);
}
在Vertex shader中做的事情很简单,将法线向量化传递给fragment shader,接着由于法线可以指向两个相反方向,它的值是介于-1到1之间,为了让输出的颜色好看些,我们用(normal + 1) * 0.5 这个公式映射到0到1之间。
![83bb77391ca677797e8daeda44eda56f.png blender 光滑组_unity shader [gamma]_11](https://s2.51cto.com/images/blog/202410/04234123_67000ca30ed7596005.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
12.9 逐顶点计算法线输出颜色的结果
在3D建模软件中,顶点之间可以进行光滑线性插值来让模型的表面更加光滑,将两个顶点之间的两个法线向量插值得出两点之间所有的法线向量值。这里以blender为例:
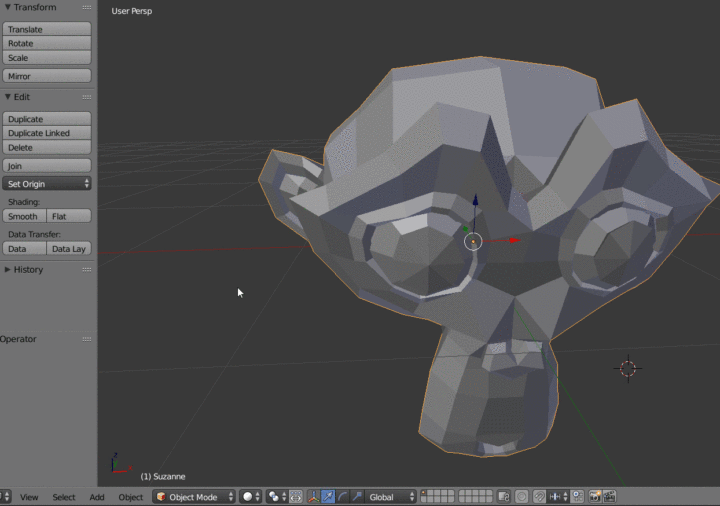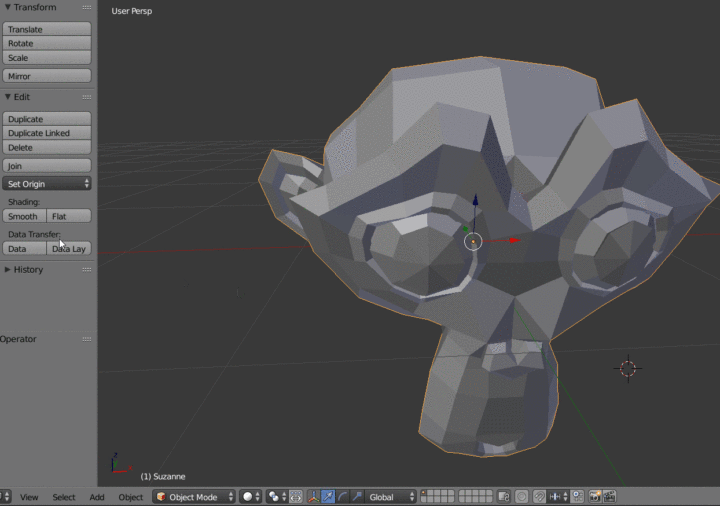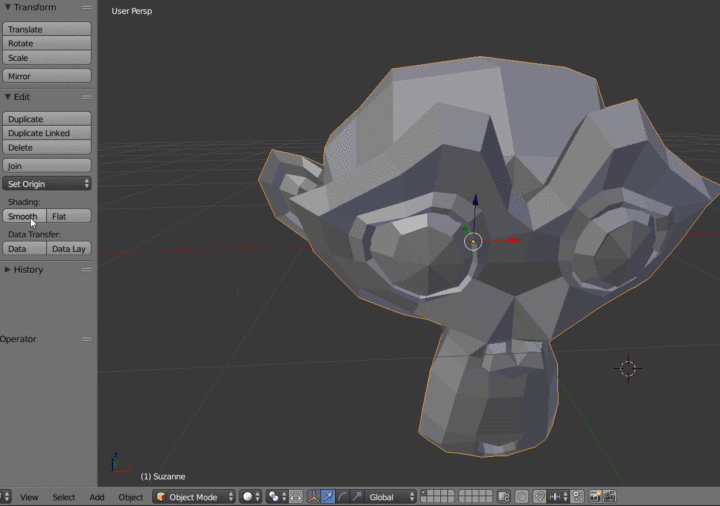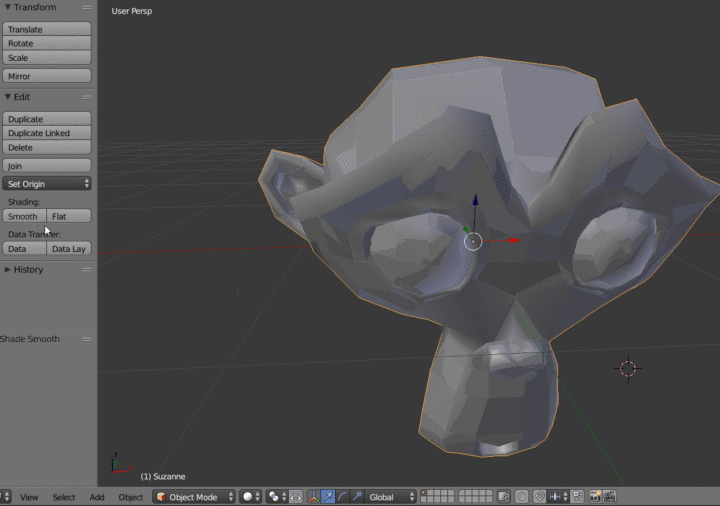
12.10 在Object Mode中对模型进行Smooth Shading处理
将同一个材质放置于光滑模型上的效果:
![db7f535b0956acfb29bff6c46f5fb2c0.png blender 光滑组_unity shader [gamma]_13](https://s2.51cto.com/images/blog/202410/04234123_67000ca389dc697401.jpg?x-oss-process=image/watermark,size_16,text_QDUxQ1RP5Y2a5a6i,color_FFFFFF,t_30,g_se,x_10,y_10,shadow_20,type_ZmFuZ3poZW5naGVpdGk=/resize,m_fixed,w_1184)
12.11 对顶点法线进行线性插值后得到的光滑模型























