python leetcode孤岛问题 leetcode用python

LeetCode题集三

• 简单题

• 100. 相同的树
• 101. 对称二叉树
• 104. 二叉树的最大深度
• 107. 二叉树的层次遍历 II
• 108. 将有序数组转换为二叉搜索树
• 110. 平衡二叉树
• 111. 二叉树的最小深度
• 112. 路径总和
• 119. 杨辉三角 II
• 119. 杨辉三角 II

---

简单题

100. 相同的树

题目：

思路：

树结构常用到递归，这里使用递归来实现。深度优先探索结点是否相同。

解法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        # 当同一个位置都为空的时候，返回True
        if not p and not q:
            return True

        # 深度优先
        if p and q and p.val==q.val:
            l = self.isSameTree(p.left, q.left)
            r = self.isSameTree(p.right, q.right)
            return l and r
        
        # 剩余的情况均为False
        return False

---

101. 对称二叉树

题目：

思路：

递归：使用额外的函数来对比左右结点，之后进行递归；
迭代：使用队列来实现，将两个对称的结点一组加入队列，然后取出进行对比判断。

解法：

• 递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:

        if not root: 
            return True

        return self.cmp_node(root.left, root.right)

    def cmp_node(self, node_1, node_2):
        if not node_1 and not node_2:
            return True
        elif not node_1 or not node_2:
            return False
        elif node_1.val != node_2.val:
            return False
        return self.cmp_node(node_1.left, node_2.right) and self.cmp_node(node_1.right, node_2.left)

• 迭代

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:

        if not root:
            return True

        # 使用队列
        queue = collections.deque()
        queue.append((root.left,root.right))

        while queue:
            left, right = queue.popleft()
            if not left and not right:
                continue
            if not left or not right:
                return False
            if left.val != right.val:
                return False
            queue.append((left.left, right.right))
            queue.append((left.right, right.left))
            
        return True

---

104. 二叉树的最大深度

题目：

思路：

递归：深度优先，如果不为空的话，深度至少是1，递归查找左右子结点可以得到答案；
迭代：广度优先，将一排结点加入到队列中然后查找他们是否存在直接点来进行计算。

解法：

• 递归（DFS）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:

        if not root:
            return 0

        left = 1 + self.maxDepth(root.left)
        right = 1 + self.maxDepth(root.right)

        return max(left, right)

• 迭代（BFS）

# BFS
    def maxDepth(self, root):

        if not root:
            return 0

        res = 0
        queue = [root]

        while queue:

            for _ in range(len(queue)):
                node = queue.pop(0)
                if node.left:
                    queue.append((node.left))
                if node.right:
                    queue.append((node.right))

            res += 1

        return res

---

107. 二叉树的层次遍历 II

题目：

思路：

递归：参考了别人的实现，主要还是深度优先实现。
迭代：与球二叉树的最大深度类似，不过最后需要的是结点的值，而不是整个结点。

解法：

• 递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
        res = []
        
        def dfs(root, depth):
            if not root:
                return []
            if len(res) < depth+1:
                res.append([])
            res[depth].append(root.val)
            dfs(root.left, depth+1)
            dfs(root.right, depth+1)
            
        dfs(root, 0)

        return res[::-1]

• 迭代

class Solution:
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []

        queue = [root]
        res = []

        while queue:

            node_values = []

            for _ in range(len(queue)):

                node = queue.pop(0)
                if node.left:
                    queue.append((node.left))
                if node.right:
                    queue.append((node.right))

                node_values.append(node.val)

            # 插在前面一层的前面
            res.insert(0, node_values)

        return res

---

108. 将有序数组转换为二叉搜索树

题目：

思路：

递归：找到根节点（中心位置）后，将左右两边继续递归，递归! 永远的神!

解法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:

        if not nums:
            return None

        mid = len(nums) // 2

        root = TreeNode(nums[mid])
        root.left = self.sortedArrayToBST(nums[:mid])
        root.right = self.sortedArrayToBST(nums[mid+1:])

        return root

---

110. 平衡二叉树

题目：

思路：

递归：计算左右子树，如果左右子树是平衡二叉树的话，再看他们的左右子树

解法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
       
    # 计算二叉树深度
    def cal_height(self, root):  
        if not root:
            return 0
        return max(self.cal_height(root.left), self.cal_height(root.right)) + 1

    def isBalanced(self, root):

        if not root:
            return True

        if abs(self.cal_height(root.left) - self.cal_height(root.right)) <= 1:
            # 判断两个子树是否都是平衡二叉树
            return self.isBalanced(root.left) and self.isBalanced(root.right)  
        else:
            return False

---

111. 二叉树的最小深度

题目：

思路：

递归：子结点为空的时候为0，子结点非空的时候为1，其他情况递归。
迭代：和层次遍历类似，一层层向下遍历，当某个结点左右子结点都为空的时候，可以跳出循环返还这个深度了。

解法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

# 递归
class Solution:
    def minDepth(self, root: TreeNode) -> int:

        if not root:
            return 0
        if not root.left and not root.right:
            return 1            
        res = inf
        if root.left:
            res = min(res, self.minDepth(root.left))
        if root.right:
            res = min(res, self.minDepth(root.right))
            
        return res+1

• 迭代：

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0

        res = 1
        queue = [root]

        while queue:

            for i in range(len(queue)):
                node = queue.pop(0)

                if node.left:
                    queue.append(node.left)

                if node.right:
                    queue.append(node.right)

                if not node.left and not node.right:
                    return res
            
            res += 1

        return res

---

112. 路径总和

题目：

思路：

递归遍历，通过逐渐减少sum值去比较。
迭代也是一样的思路，不过得使用一个栈。

解法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def hasPathSum(self, root: TreeNode, sum: int) -> bool:

        if not root:
            return 0

        if not root.left and not root.right:
            return root.val == sum    
        
        return self.hasPathSum(root.left, sum - root.val) or self.hasPathSum(root.right, sum - root.val)

• 迭代

class Solution:
    def hasPathSum(self,root,sum):
        if not root:
            return False
        stack = [(root,sum)]
        while stack:
            node, val = stack.pop()
            if not node.left and not node.right and node.val == val:
                return True
            if node.right:
                stack.append((node.right,val-node.val))
            if node.left:
                stack.append((node.left,val-node.val))
        return False

---

119. 杨辉三角 II

题目：

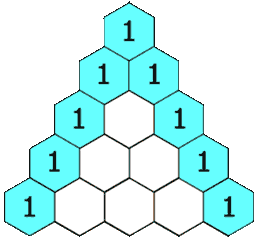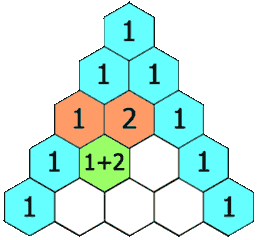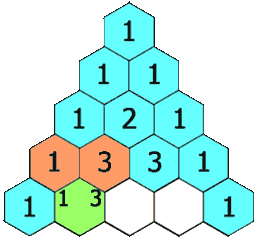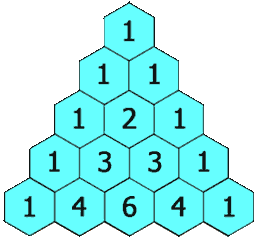
思路：

：按照给的规律直接暴力求解
巧妙求解：参考了别人的答案，可以错位相加求解

解法：

• 暴力求解

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:

        if not numRows:
            return []

        res = [[1]]

        for i in range(1, numRows):
            tmp = [1, 1]

            for j in range(1, i):
                num = res[i - 1][j - 1] + res[i - 1][j]
                tmp.insert(j, num)

            res.append(tmp)

        return res

• 巧妙求解

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        if numRows == 0: 
        	return []
        res = [[1]]
        while len(res) < numRows:
            newRow = [a+b for a, b in zip([0]+res[-1], res[-1]+[0])]
            res.append(newRow)      
        return res

---

119. 杨辉三角 II

题目：

思路：

在上那个一题的基础上修改实现。

解法：

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:

        res = [[1]]

        while len(res) <= rowIndex:
            newRow = [a + b for a, b in zip([0]+res[-1], res[-1]+[0])]
            res.append(newRow)      
        return res[rowIndex]

---