接雨水解法详解:
题目:

基本思路:从图上可以看出要想接住雨水,必须是凹字形的,也就是当前位置的左右两边必须存在高度大于它的地方,所以我们要想知道当前位置最多能存储多少水,只需找到左边最高处max_left和右边最高处max_right,取他们两个较小的那边计算即可(短板效应)。
其实接下来的解法要解决的问题就是如何找到max_right和max_left。
不过我们首先来看一个无法AC的解法:
解法一:按行
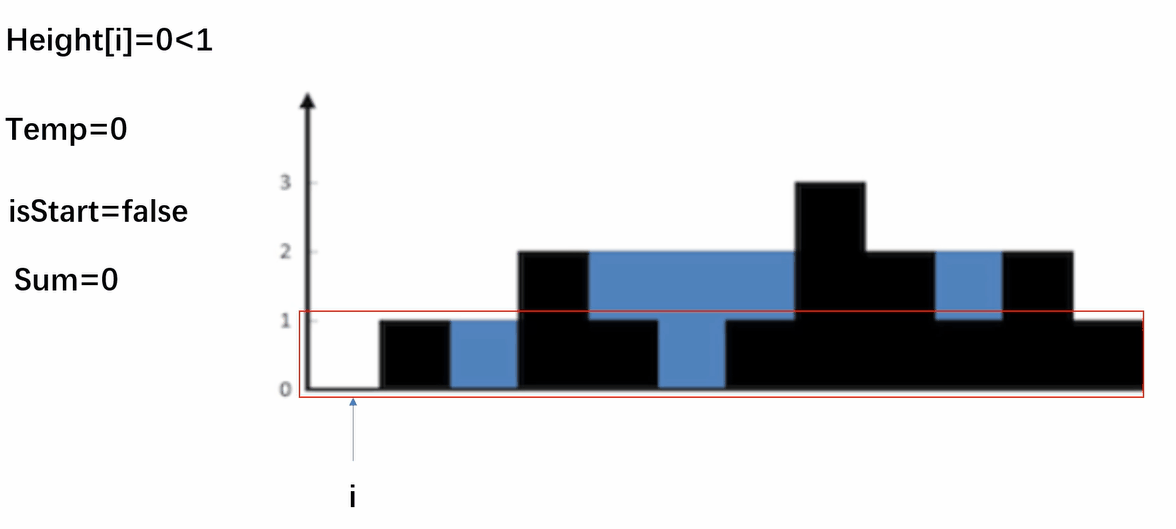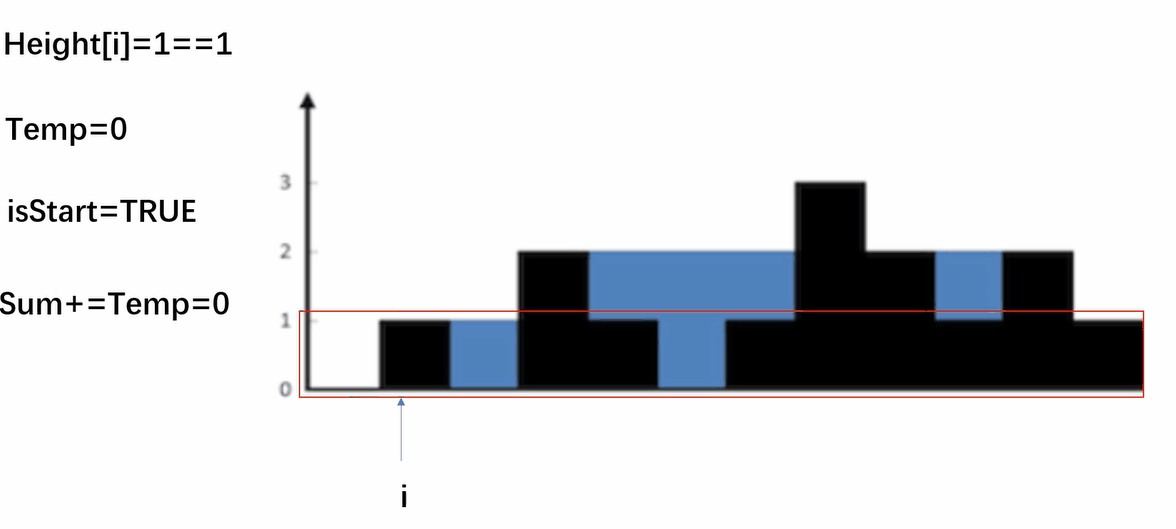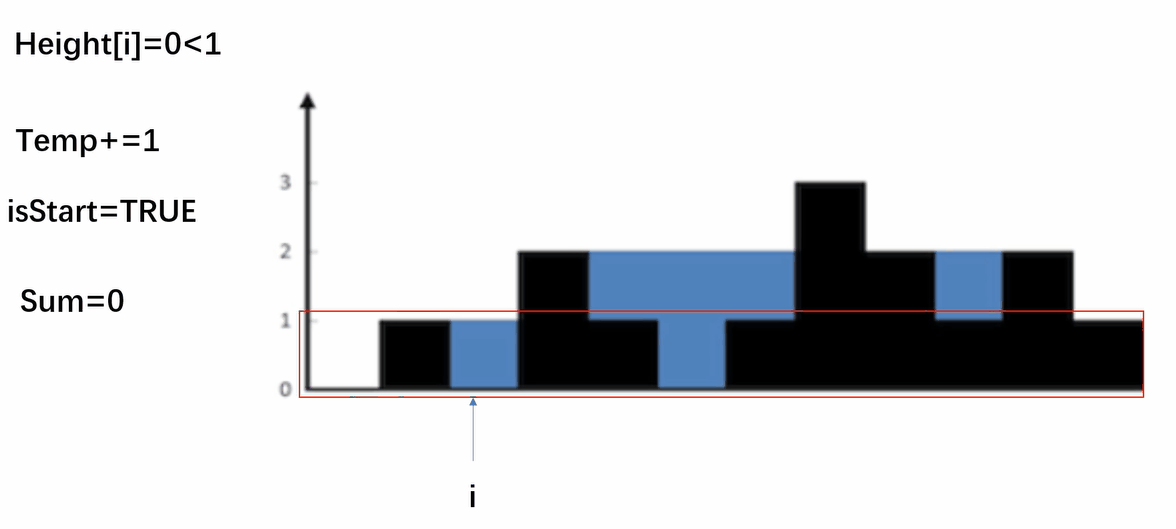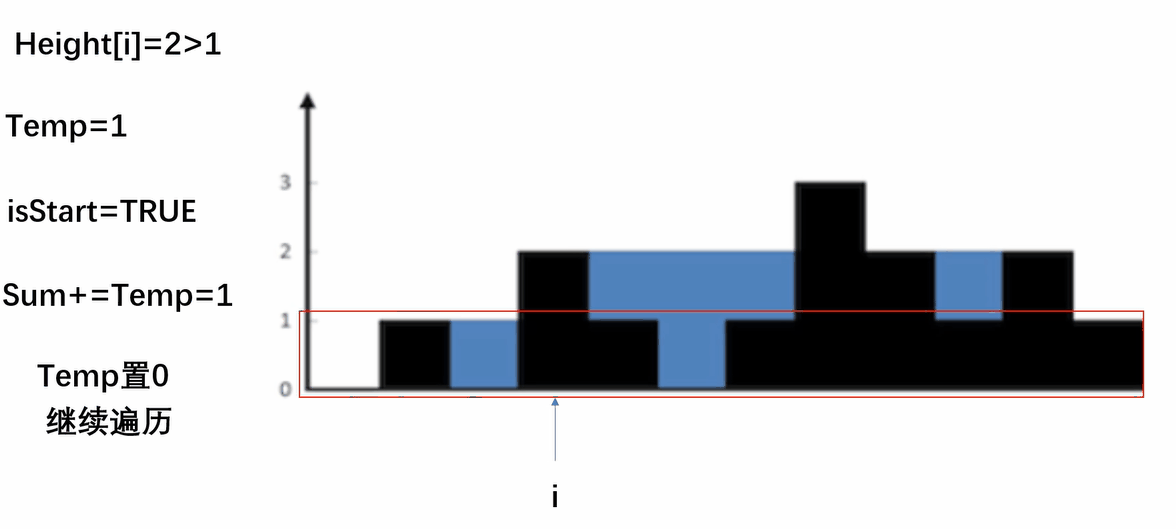
按行顾名思义就是一行一行地进行计算,首先我们计算第一行,设置一个变量temp临时存储当前接的水和开始标志isStart,当碰到第一个高度大于等于行数的位置时,temp置0,开始计算,接下来如果碰到小于行数的位置时,temp+1,碰到大于行数的位置时,temp置0,继续往后遍历,如此遍历完一行继续遍历下一行。
class Solution {
public int trap(int[] height) {
int sum = 0;
int max = getMax(height);//找到最大的高度,以便遍历。
for (int i = 1; i <= max; i++) {
boolean isStart = false; //标记是否开始更新 temp
int temp_sum = 0;
for (int j = 0; j < height.length; j++) {
if (isStart && height[j] < i) {
temp_sum++;
}
if (height[j] >= i) {
sum = sum + temp_sum;
temp_sum = 0;
isStart = true;
}
}
}
return sum;
}
private int getMax(int[] height) {
int max = 0;
for (int i = 0; i < height.length; i++) {
if (height[i] > max) {
max = height[i];
}
}
return max;
}
}不过此解法会在最后两个测试用例处,TLE掉,我们只需了解一下这种思想,medium难度的题还是可以过的。
解法二:按列
这个解法就是我们刚开始所说思路的最朴素的解法了,要求i位置接水量,只需找到i左边最高位置的高度max_left和右边最高位置的高度max_right,然后取较小的那个min_height=min(max_right,max_left),最后计算i位置接水量:min_height-height[i],当然如果min_height<height[i],就不用计算啦。

class Solution {
public int trap(int[] height) {
int ans=0;
for(int i=1;i<height.length-1;i++){//第一个和最后一个位置肯定存不了水
int max_left=0;
for(int j=i-1;j>=0;j--){//找到当前位置左边最高处
max_left=Math.max(max_left,height[j]);
}
int max_right=0;
for(int j=i+1;j<height.length;j++)//找到当前位置右边最高处
max_right=Math.max(max_right,height[j]);
int min_high=Math.min(max_right,max_left);
if(min_high>height[i]){
ans+=min_high-height[i];
}
}
return ans;
}
}解法三:动态规划
我们知道解法二每到一个位置都会遍历左右两边来寻找它的左右最高处,这样就会导致O(n^2)的时间复杂度,我们能不能事先就找好每个位置对应的max_left和max_right,显而易见是可以的,所以我们需要声明两个数组max_left和max_right来存储每个位置对应的左右最高点,因为我们只在它左右两边寻找,我们可以写出当前位置i的max_left[i]=max(max_left[i-1],height[i-1]),右边同理,接下来就是和解法二一样了。
class Solution {
public int trap(int[] height) {
int[] max_left=new int[height.length];
int[] max_right=new int[height.length];
int ans=0;
for(int i=1;i<height.length-1;i++){
max_left[i]=Math.max(max_left[i-1],height[i-1]);
}
for(int i=height.length-2;i>=1;i--){
max_right[i]=Math.max(max_right[i+1],height[i+1]);
}
for(int i=1;i<height.length-1;i++){
int min_height=Math.min(max_right[i],max_left[i]);
if(min_height>height[i]){
ans+=min_height-height[i];
}
}
return ans;
}
}解法四:双指针
从动态规划解法可以看出,只要max_left[i]<max_right[i],积水的高度由max_left[i]决定,也就是积水的高度是由较低的那边决定,所以此时我们应该继续由较低->较高那个方向遍历,直到此时较低的这边发现比另一边更高的位置,再转换方向,这样我们就可以一次遍历且只需两个指针便可完成计算。
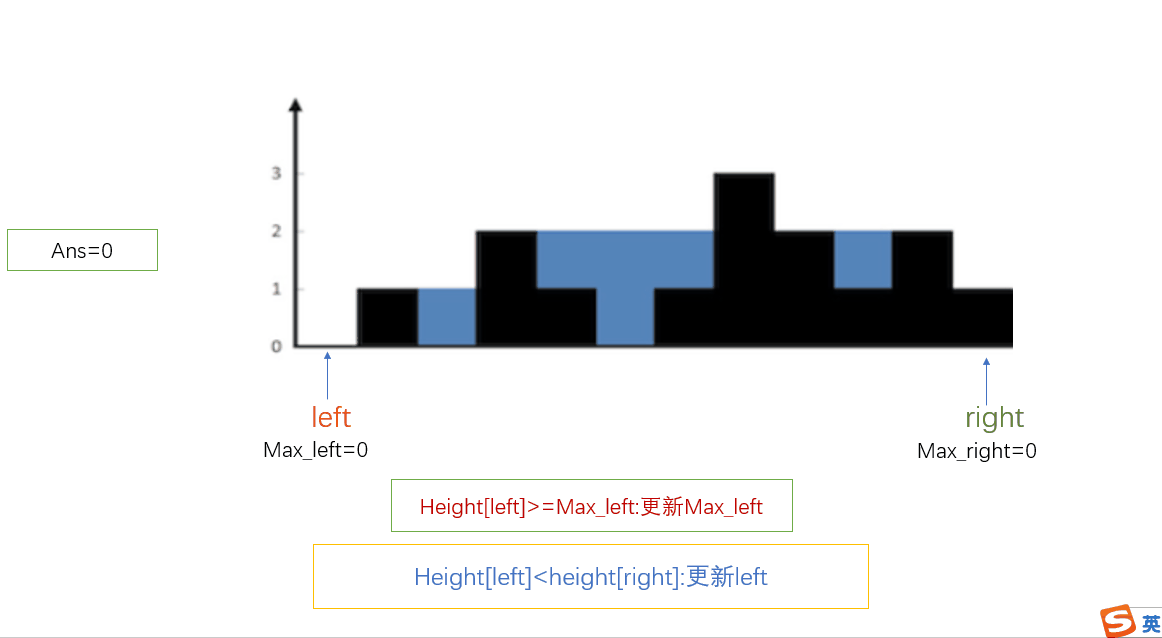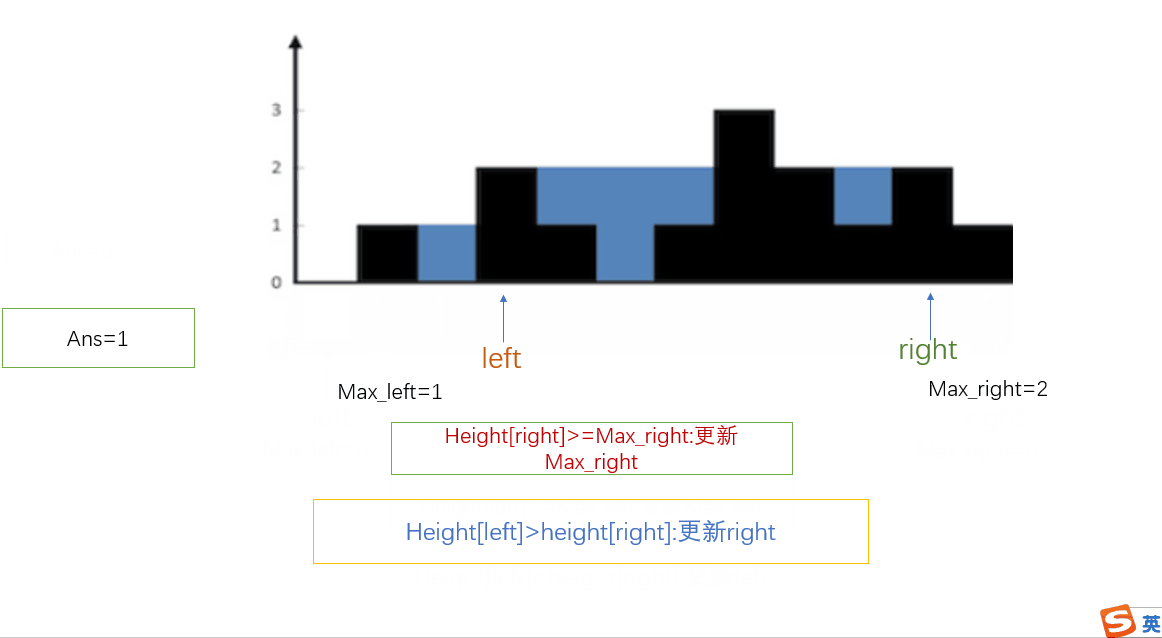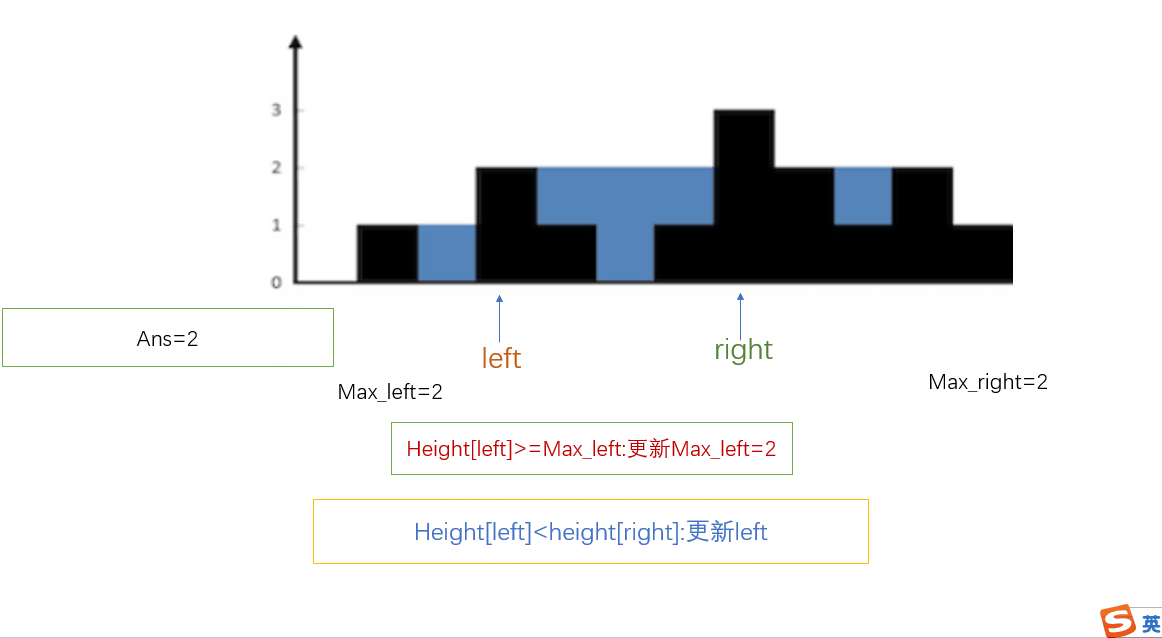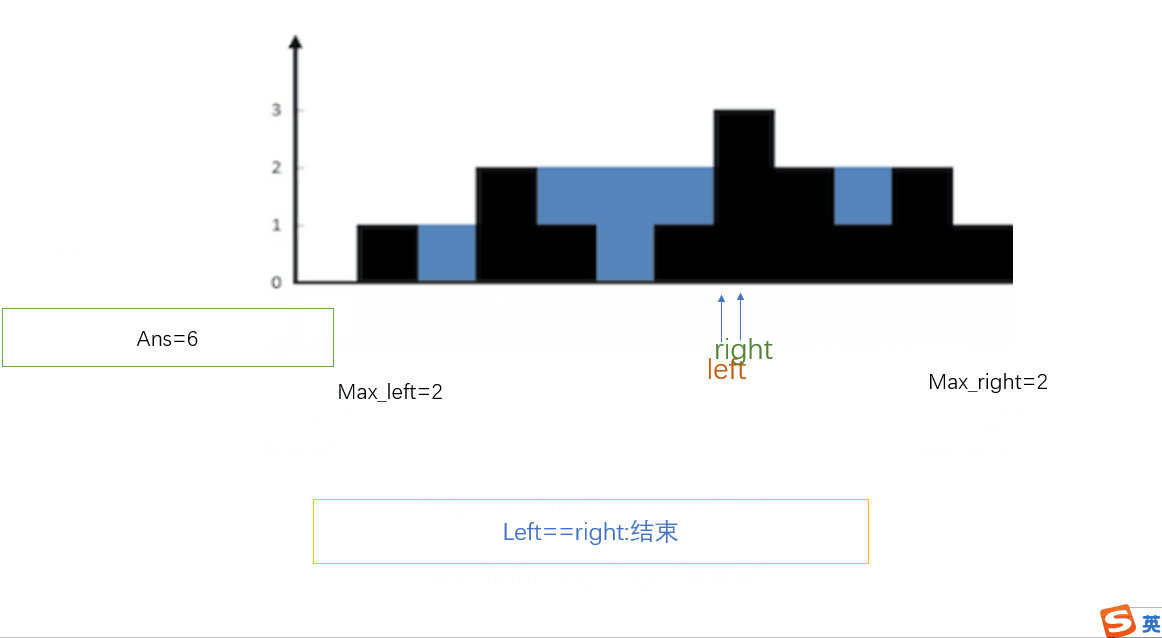
- 初始化 left 指针为 0 并且 right 指针为 size-1
-
While left<right, do:If height[left] < height[right]If height[left]≥left_max, 更新 left_maxElse left_max−height[left] 到ansleft = left + 1. -
ElseIf height[right]≥right_max, 更新 right_maxElse 累加 right_max−height[right] 到 ansright = right - 1.
int trap(vector<int>& height)
{
int left = 0, right = height.size() - 1;
int ans = 0;
int left_max = 0, right_max = 0;
while (left < right) {
if (height[left] < height[right]) {
height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
++left;
}
else {
height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
--right;
}
}
return ans;
}解法五:单调栈
思路:单调栈可以保证栈底到栈顶是单调递减的,也就是说栈顶元素可以由它前一个元素所界定,我们遍历数组时可以维护一个单调栈来存储索引,当当前元素小于栈顶元素时,入栈,当当前元素大于等于栈顶元素时,此时栈顶元素的接水量就取决于其前一个元素和当前元素较小的那个,栈顶元素出栈。
算法:
- 使用栈来存储条形块的索引下标。
- 遍历数组:
- 当栈非空且 height[current]>height[st.top()]
- 意味着栈中元素可以被弹出。弹出栈顶元素
- 计算当前元素和栈顶元素的距离,准备进行填充操作
distance=current−st.top()−1
- 找出界定高度
- bounded_height=min(height[current],height[st.top()])−height[top]
- 往答案中累加积水量ans+=distance×bounded_height
- 将当前索引下标入栈
- 将 current 移动到下个位置
int trap(vector<int>& height)
{
int ans = 0, current = 0;
stack<int> st;
while (current < height.size()) {
while (!st.empty() && height[current] > height[st.top()]) {
int top = st.top();
st.pop();
if (st.empty())
break;
int distance = current - st.top() - 1;
int bounded_height = min(height[current], height[st.top()]) - height[top];
ans += distance * bounded_height;
}
st.push(current++);
}
return ans;
}总结:
这种多解法的题目可以尽量去了解它的每一种解法,这对扩展自己的解题思维有很大的帮助,其实这个题目这么多解法大部分都是在解决怎么高效找出左右两边最高点,时间复杂度由O(n^2)提升到O(n),空间复杂度也由O(n)->O(1),所以有时候很多方法都是由暴力逐渐改善的,本人表达可能词不达意,还请谅解,如有任何问题,请留言指出,不甚感激。





















