关于快速排序算法最多比较次数与最少比较次数的问题
最常见的快速排序算法的衡量标准是时间复杂度,即最坏情况 \(O(n)\) ,最优与平均情况均为 \(O(n\ log_2^n)\)
对 50 个整数进行快速排序需进行的关键码之间的比较次数可能达到的最大值和最小值分别是多少?
最好情况与最坏情况
快速排序的情况好坏取决于一趟划分后枢轴量的位置。枢轴量划分的越均匀就越好,越不均匀也就越差。
最大比较次数
最大比较次数出现在最坏情况,也就是初始序列完全有序的情况。这种情况下每次划分都是最不均匀的,即一边是零个另一边是全部。可以参考下面十个元素的例子,这种情况比较次数轻易可以看出是 \(1+2+3+\dots+(n-1)=\frac{n(n-1)}{2}\)

最小比较次数
最小比较次数出现在最好情况,即每次枢轴量都可以完美均分序列(我称之为完美枢轴),即每一趟枢轴都会刚好在正中间,例如:
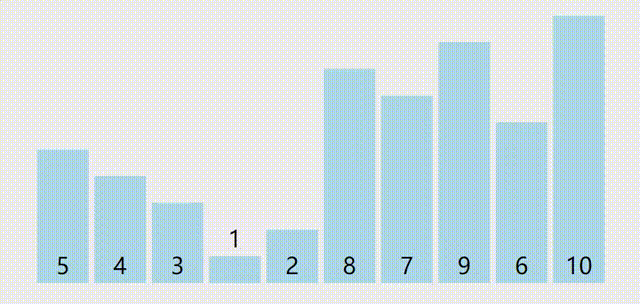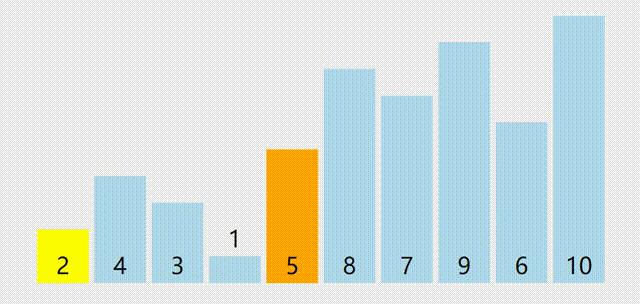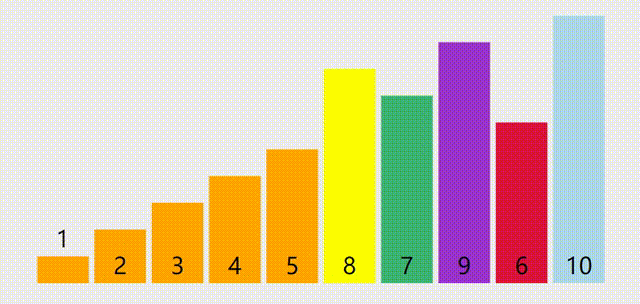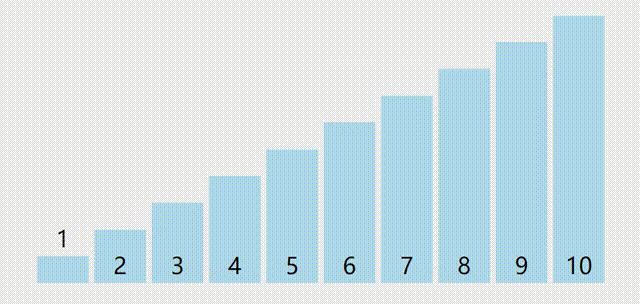
此种情况下不太好直接计算比较次数,可以使用递推的方法进行计算,如果我们把对 \(n\) 个元素进行快排的最小比较次数记为 \(best(n)\)。首先列出元情况,也就是 0 个元素和 1 个元素的情况:
\[best(0) = 0\qquad best(1) = 0 \]
则可以利用公式
\[\begin{align} best(n) &= 枢轴归位所需比较次数 + best(枢轴归位后左半部分) + best(枢轴归位后右半部分)\\ &= \qquad(n-1) \qquad\ \quad+ \qquad best(\left\lfloor\frac{n-1}{2} \right\rfloor) \quad\ \ + \qquad best(\left\lfloor\frac{n}{2} \right\rfloor)\\ \end{align} \]
一步步递推下去:
\[best(2) = 1 + best(0) + best(1) = 1\\ best(3) = 2 + best(1) + best(1) = 2\\ best(4) = 3 + best(1) + best(2) = 4\\ \dots \]
回归题目,对 50 个整数进行快速排序需进行的关键码之间的比较次数可能达到的最小值为:
\[\begin{align} best(50) &= 49 + best(24) + best(25)\\ &= 49 + 23 + best(11) + best(12) + 24 + best(12) + best(12) \\ &= 49 + 23 + 24 + best(11) + 3\times best(12)\\ &= 49 + 23 + 24 + 10 + best(5) + best(5) + 3\times (11 + best(5) + best(6))\\ &= 49 + 23 + 24 + 10 + 33 + 5\times best(5) + 3\times best(6)\\ &= 49 + 23 + 24 + 10 + 33 + 5\times(4 + best(2) + best(2)) + 3\times(5 + best(2) + best(3))\\ &= 49 + 23 + 24 + 10 + 33 + 20 + 15 + 13\times best(2) + 3\times best(3)\\ &= 49 + 23 + 24 + 10 + 33 + 20 + 15 + 13\times best(2) + 3\times(2 + best(1) + best(1))\\ &= 49 + 23 + 24 + 10 + 33 + 20 + 15 + 6 + 13\times best(2) + 6\times best(1)\\ &= 49 + 23 + 24 + 10 + 33 + 20 + 15 + 6 + 13\times 1 + 6\times 0\\ &=193 \end{align} \]





















