这两天内心有点不平静,不是很想学新东西。准备写一个算法和数据结构的系列做个总结。 内容主要来自《算法导论》和Robert Sedgewick的《算法》(强烈推荐这本书)一些简单的基本内容就不再赘述(例如链表定义,基本的排序算法等等)。
下面我们讨论红黑树,这里我们假定大家已经学习和掌握了二叉查找树和2-3树。
大家知道二叉查找树的查找性能是不稳定的,如果一颗二叉查找树只有左子树或者右子树,那它实际上就成为了一个排序链表,查找复杂度为O(n)(即遍历单链表)。而我们又不能够避免这一现象的发生,因此我们需要考虑将二叉查找树进行优化。下面介绍的红黑树就是这一的一种数据结构,它能够保证数据的查找效率为O(log n)。
1.红黑树定义
定义一(最常见的定义,《算法导论》的红黑树,下面我们主要讨论这个红黑树):
- 每个结点要么是红的要么是黑的。
- 根结点是黑的。
- 每个叶结点(叶结点即指树尾端NIL指针或NULL结点)都是黑的。
- 如果一个结点是红的,那么它的两个儿子都是黑的。
- NIL指针的每条路径都包含相同数目的黑结点。(我们下面称这个数目为树的黑高度)
由上面的第4条我们能够感觉出这棵树的大部分节点都是黑的。
在树的最长路径上,不存在相邻的红节点,因此最长路径的长度至多为黑高度的二倍(每一个红节点的父亲都是黑的,因此红节点个数≤黑节点个数,总长度=红节点个数+黑节点个数≤2*黑节点个数)。这一性质保证了树大致是平衡的(不会出现只有左子树或右子树的情况)。
定义二(《算法》的红黑树定义):
- 每个结点要么是红的要么是黑的 (我们称红节点与它父节点的链接为红链接)。
- 根结点是黑的。
- 红节点均为左链接
- 没有任何一个节点同时和两条红链接相连
- 树是完美黑平衡的,即任意空链接到根节点路径上的黑链接数量相同
2.红黑树的本质
定义一的红黑树的实际上是一颗2-3-4树。
由于树形结构在计算机上不易表示,因此我会以图片的形式上传。这里我们约定□(方块)代表红节点,○(圆圈)代表黑节点。
这是一颗红黑树:
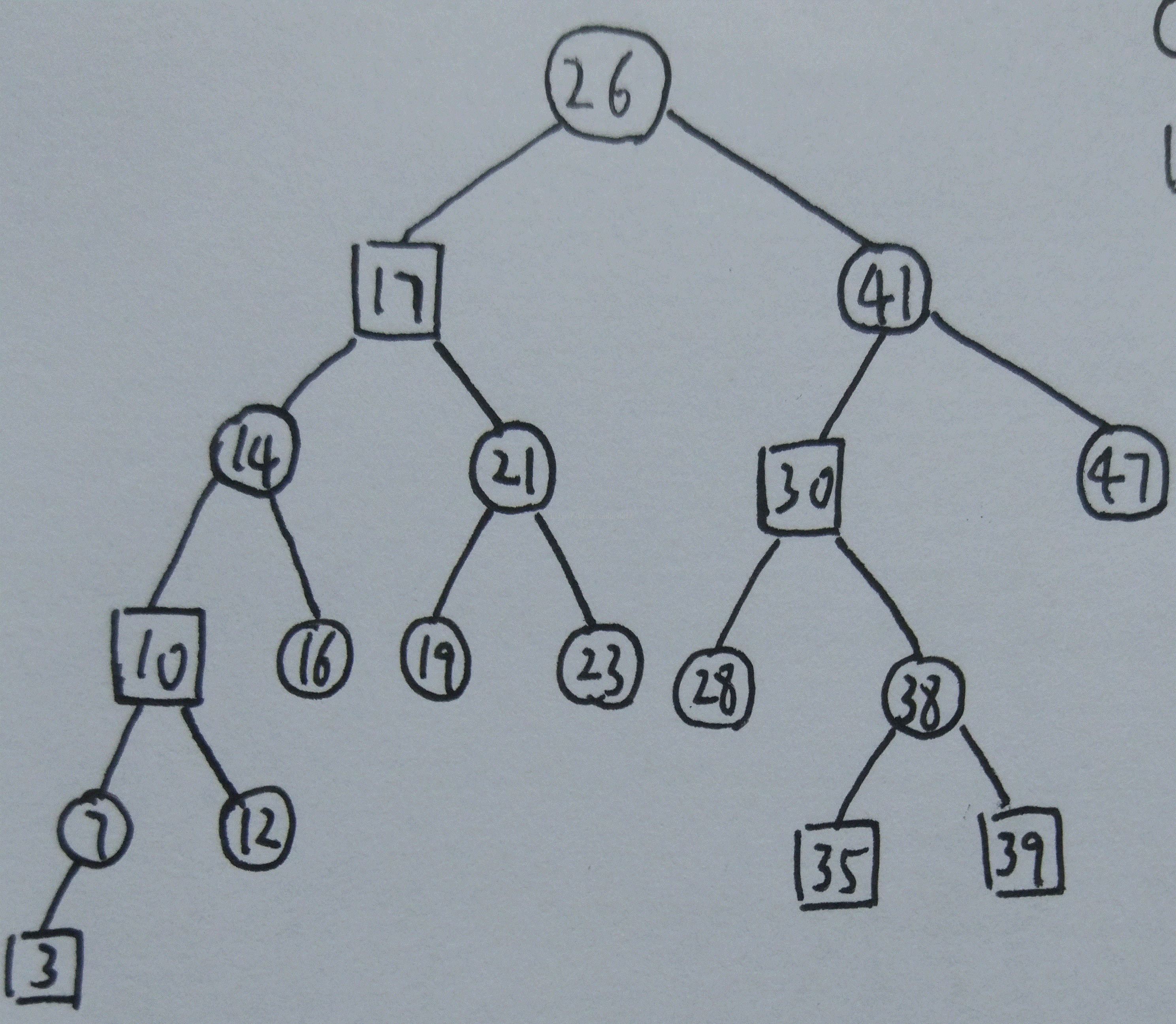
我们定义红链接为红节点与它父节点的链接,我们尝试画平所有的红链接:
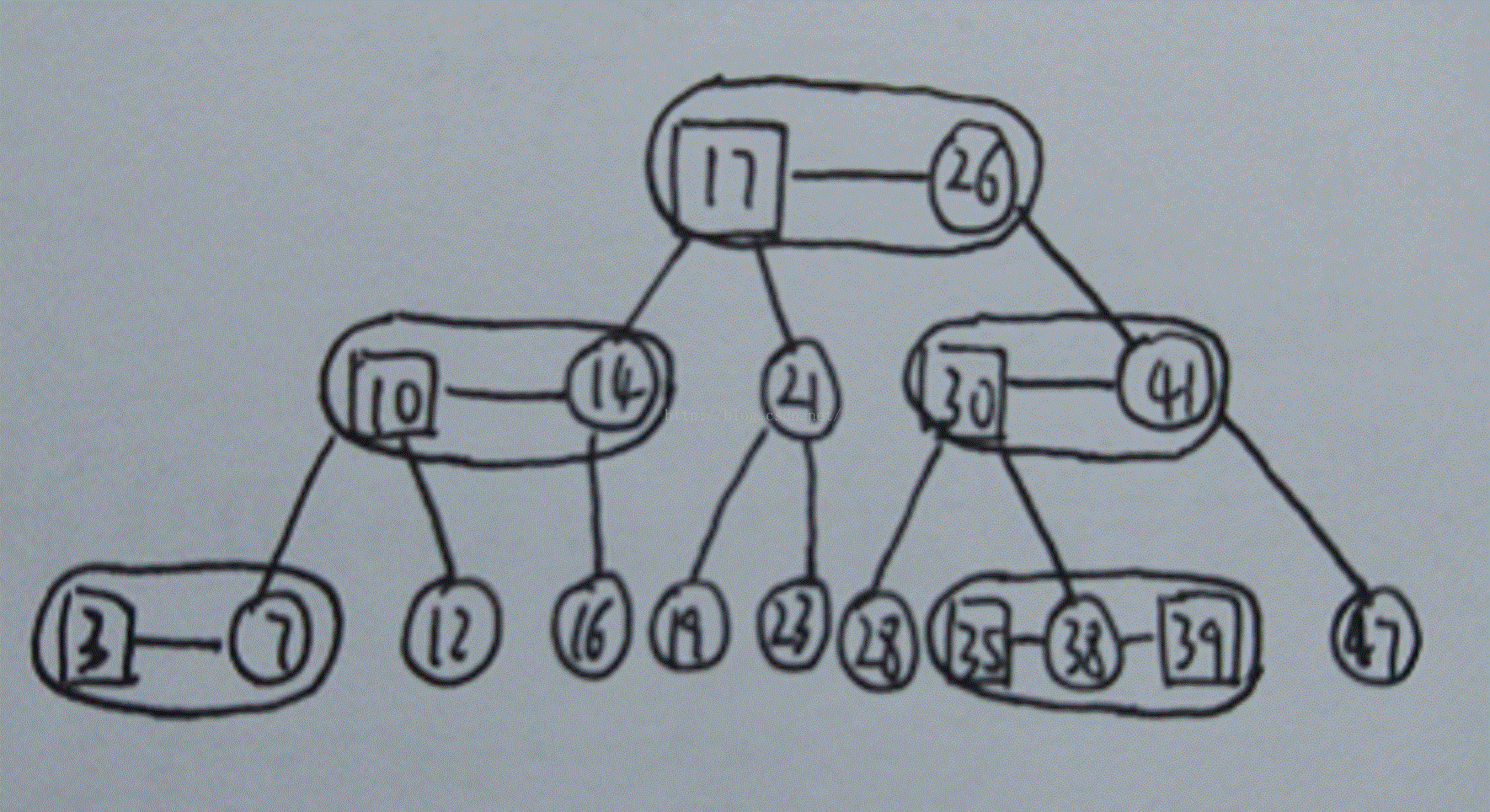
看着有点乱?我们忽略大节点内部的链接,得到了一颗2-3-4树:
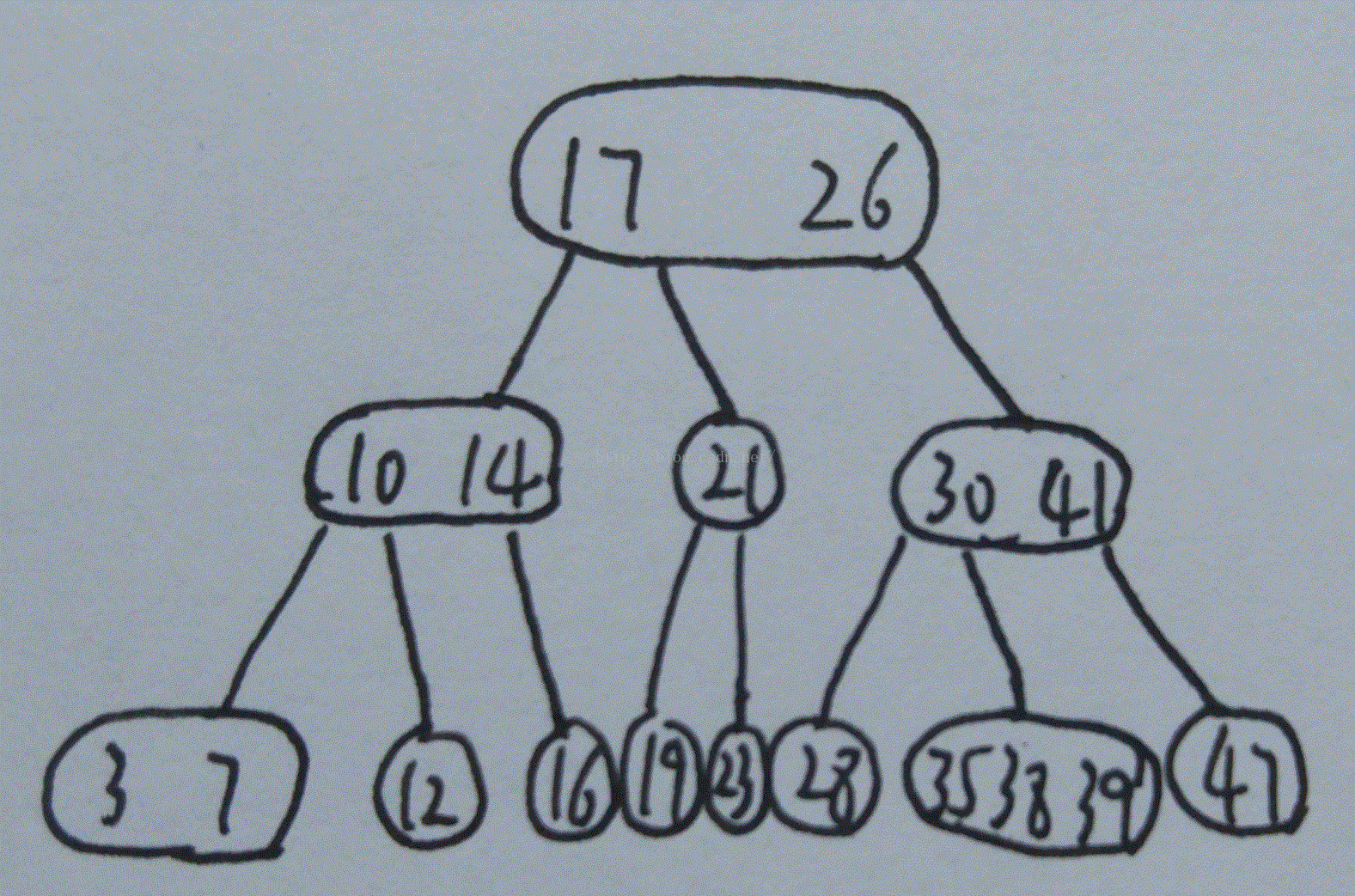
4节点在红黑树中的形状是这样的(黑节点的两个孩子均为红节点,这三个节点即为一个4-节点):
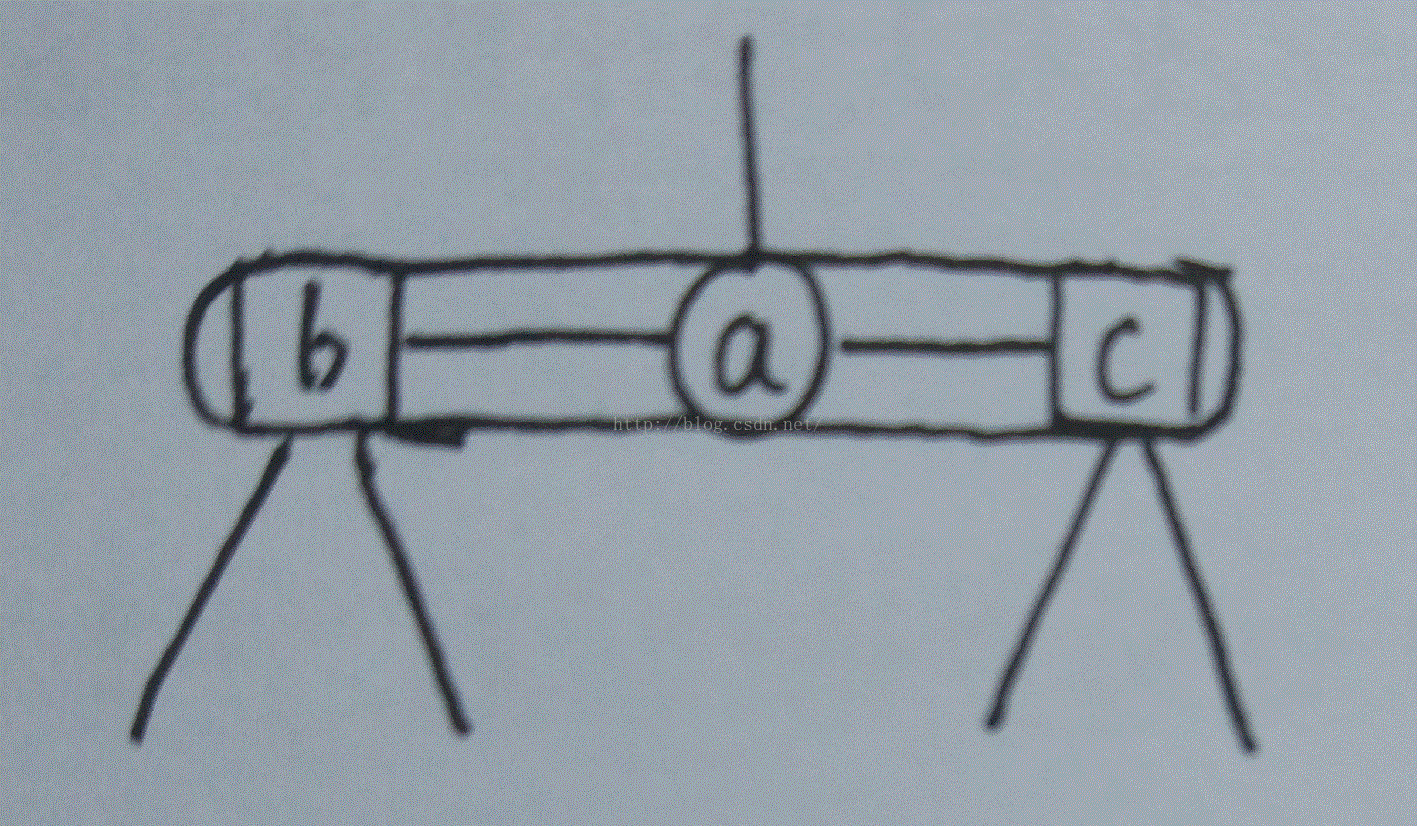
3-节点形状是这样的:
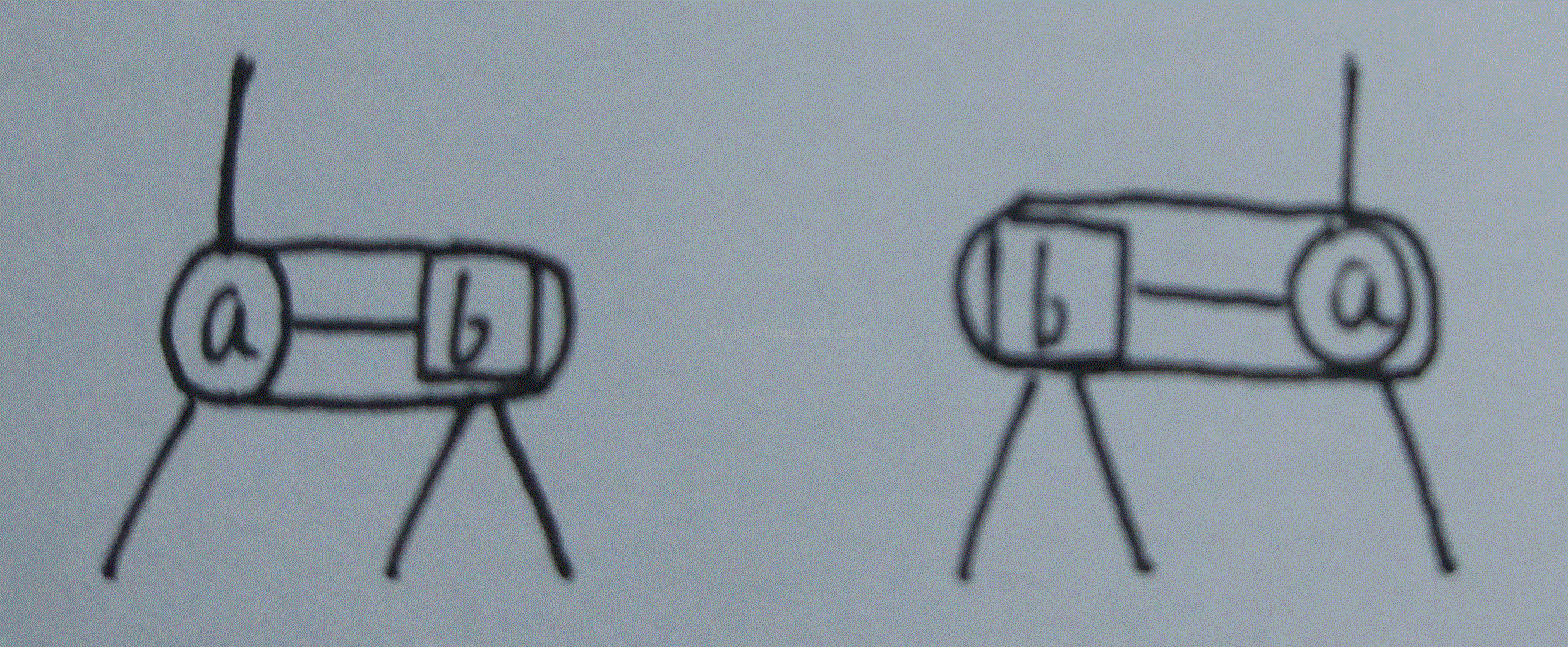
3.红黑树基本操作
红黑树既然能够保证查找的高效,那么在进行插入和删除的时候就肯定不能像普通的二叉查找树那么随意了,为了保证红黑树的平衡,我们可能会进行调整从而保证树的黑高度相同这一特性。
我看过的许多博客对红黑树的插入和删除都是直接介绍了右旋左旋然后插入怎么旋转删除怎么旋转,尤其是删除的时候往往比较复杂,很容易丧失学习的主动性。下面我们来介绍红黑树的插入删除操作并说明为什么要这么做。
由于红黑树的本质是一颗2-3-4树,因此我们只需将2-3-4树的插入删除方式对应到红黑树即可。这里我们先介绍两个操作,左旋和右旋:
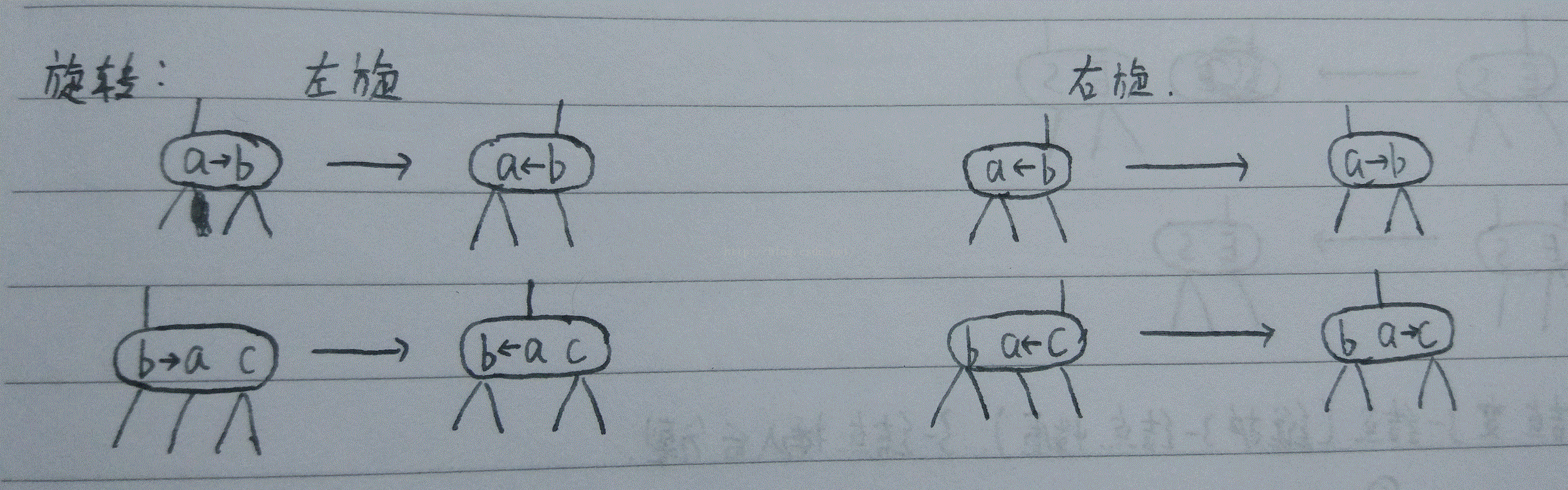
代码如下:
Left_Rotate(TreeNode a)
{
b = a.right;
a.right = b.left;
b.left = a;
//如果有父节点的指针
b.parent = a.parent;
a.parent = b;
//如果没有父节点的指针,让上面的方法返回新节点的引用(return b),执行p = Left_Rotate(p)即可
}
Right_Rotate(TreeNode b)
{
a = b.left;
b.left = a.right;
a.right = b;
return a;
}
插入
当我们插入一个节点时,我们默认插入一个红节点
插入到2-节点,直接插入变为3-节点
插入到3-节点,插入变为4-节点(需要调整4-节点形状)
插入到4-节点,将4-节点向上分裂为两个2-节点
下面这个例子涉及到了所有的情况:
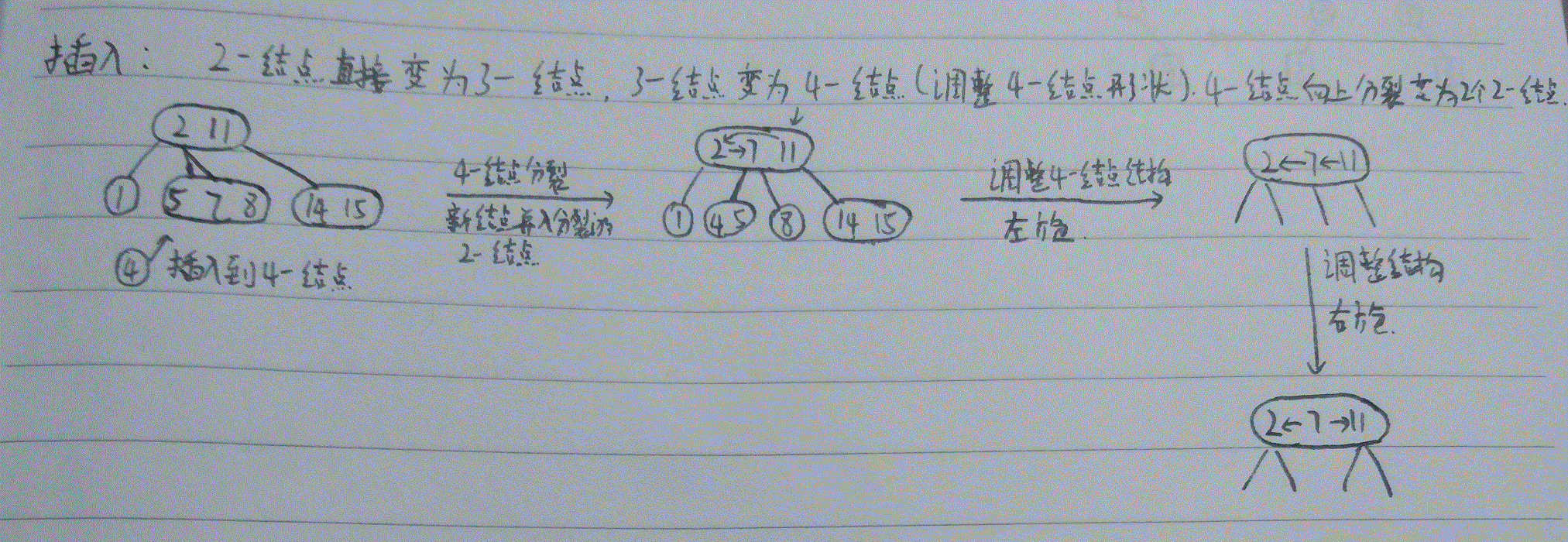
删除
首先,我们删除二叉查找树的节点时,一般是找它的中序遍历的前节点(左子树的最右节点)或者后节点(右子树的最左节点)来替代,因此我们实际上删除的是叶子节点。
当删除的叶节点是红节点(3-节点或4-节点)时,直接删除不会影响红黑树的平衡。
当删除节点是叶节点是,有以下3种情况(这里我们假设实际删除的节点是目标节点的后继):
这里我们假定节点已被删除,树A的高度比他的兄弟节点高度少1。
1.A的兄弟节点为3-节点或4-节点:
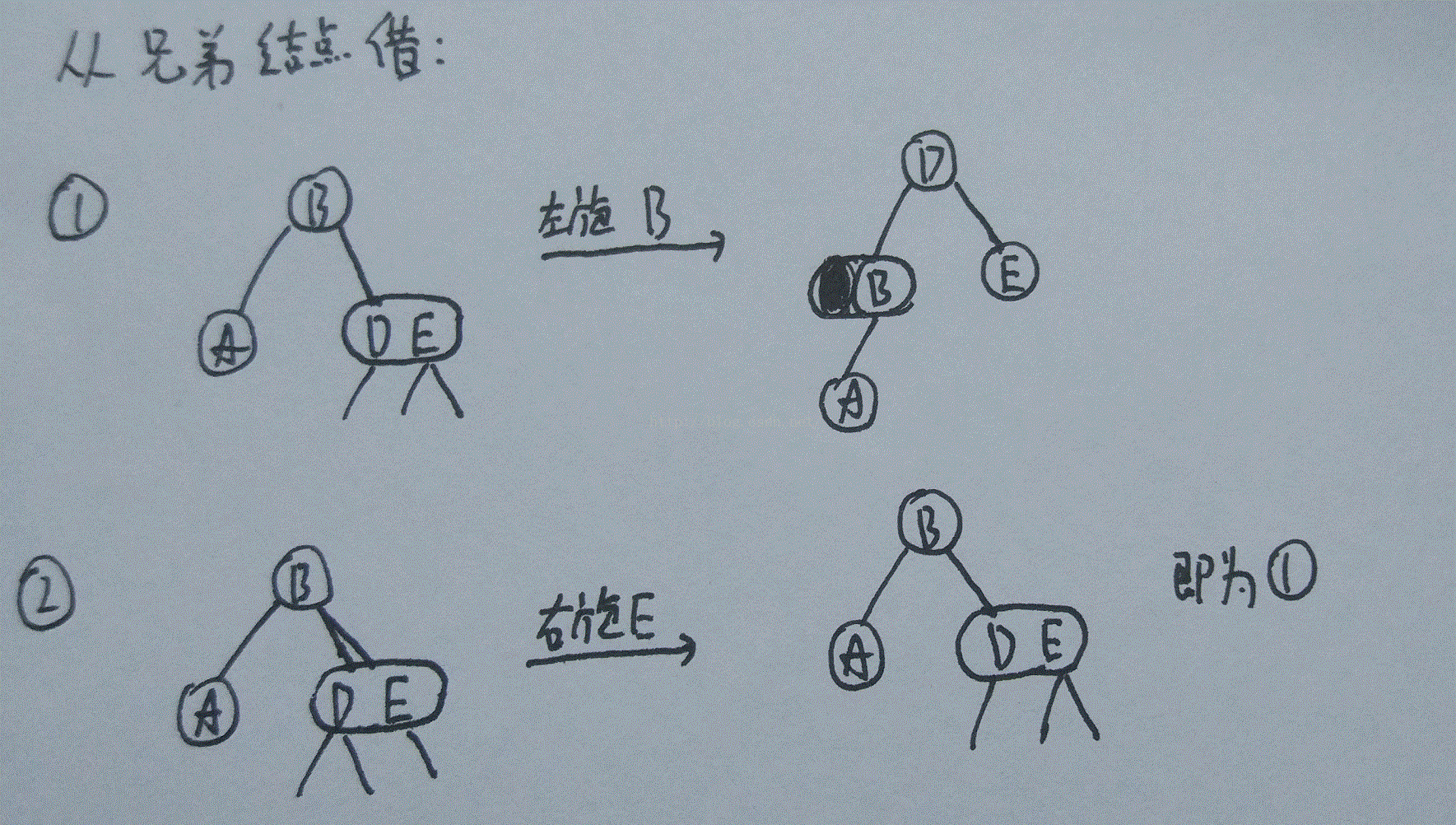
2.A的父节点为3-节点或4-节点:
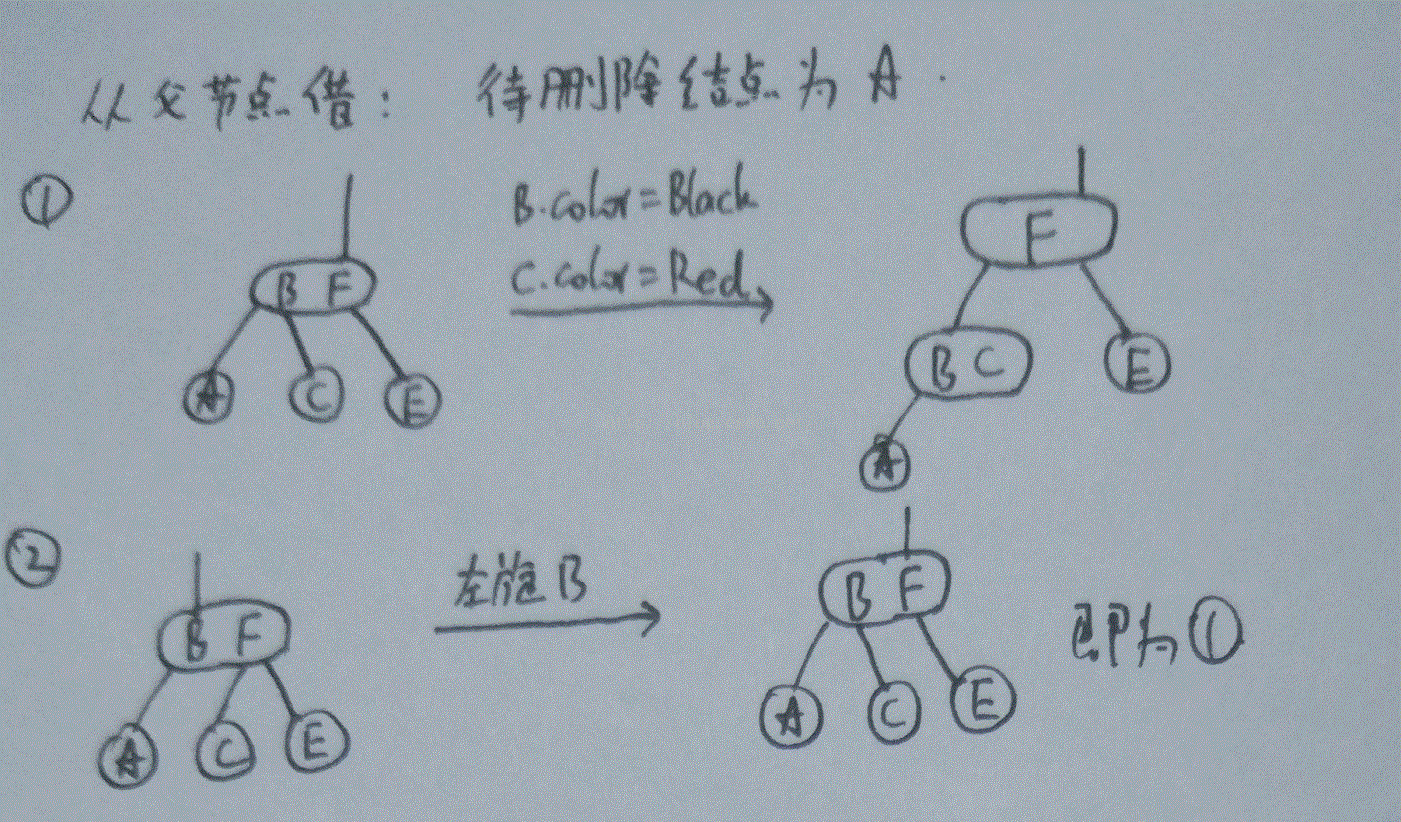
3.父节点和兄弟节点都是2-节点:
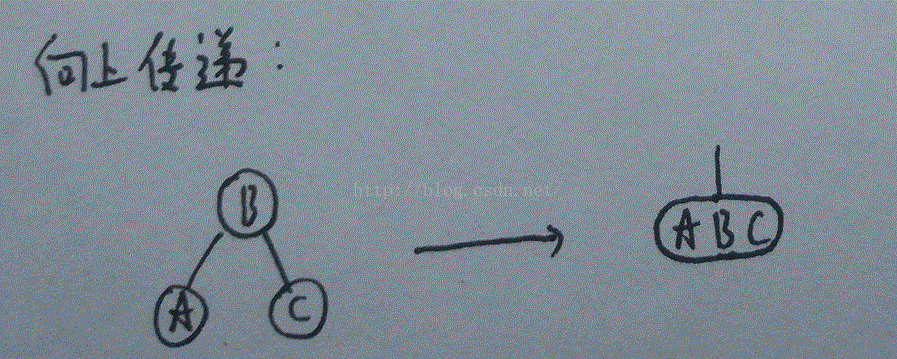
我们把这个问题传递到了B的父节点,一直传递到根节点或者出现上述两种情况之一。
PS:前面红黑树的定义二要求红链接为左链接,这种约定可以简化许多插入和删除的操作。(这棵树是2-3树而不是2-3-4树)有兴趣的同学可以去看《算法》这本书。





















