文章目录
- 一.什么是数据聚类
- 二.基于GMM的聚类
- 三.k-means聚类法
- 四.层次凝聚聚类
- 五.DBSCAN聚类法
一.什么是数据聚类
如果我们想要对全部都是无标签的数据进行分类,这时候数据聚类就是一大类方式。聚类的意思顾名思义,按照一定的法则,将部分“相近的”数据聚成同一类,给它们相同的标签即可。
下面介绍几种比较有代表性的聚类方法。文章中的GIF图来源于以下文章:https://www.sohu.com/a/225353030_99992181。
二.基于GMM的聚类
在半监督学习中我们已经讲过在部分数据有标签的情况下如何用GMM进行所谓的样本训练了。在这里,我们要自己去定义类的数量,之后随机初始化对应的多元高斯分布,然后以同样的操作使用EM算法即可。(当然最开始计算每个类别出现的概率,这个也可以随机,一般是每个类别的数量相同)
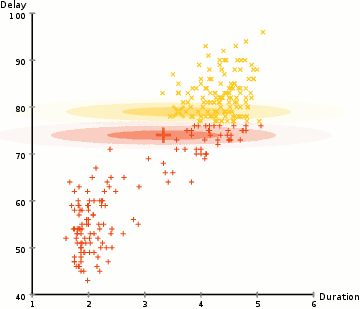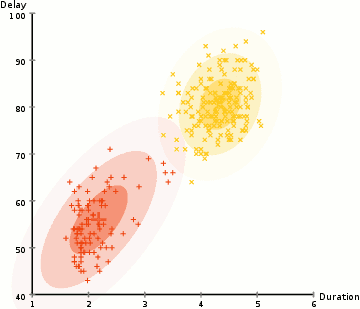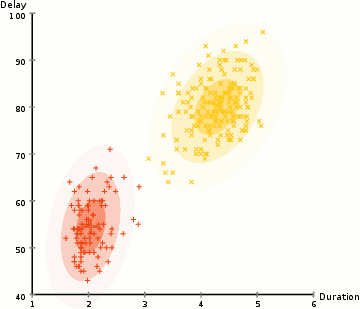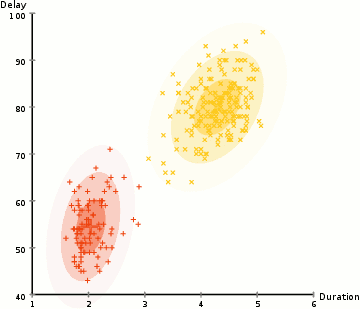
由于EM算法本身是收敛的,因此这样做我们可以保证最后的结果是收敛的。
这种方法的优点在于我们不仅可以知道每个点在哪个类,我们还可以知道每个点在所有类的概率,非常的舒服,变为了连续型的数据。但缺点在于我们还是不知道到底应该分成多少类,而且这样做确实是比较麻烦的。
三.k-means聚类法
我们将基于GMM的聚类法进行简化,不再关注后验概率,而只是通过计算每个点到各个聚类中心的距离,来确定每个点该分到哪个类,然后同样使用EM算法来通过不断地迭代来收敛。
因此算法的步骤如下:
1.初始化聚类的数量和聚类中心,一般来说我们都会选择比较分散的几个点作为聚类中心。将数据的每个维度的量纲进行标准化,保证几何距离有意义。
2.(E步)计算每个点到聚类中心的距离,距离的定义可以自己决定,一般是几何距离;之后标记到对应的类别中。
3.(M步)通过对每个类别中所有的点取平均,来更新聚类中心。如果每个中心的移动距离改变的很小或者没有改变(这时说明E步每个点的标签都没有改变),那算法结束;否则回到第2步。
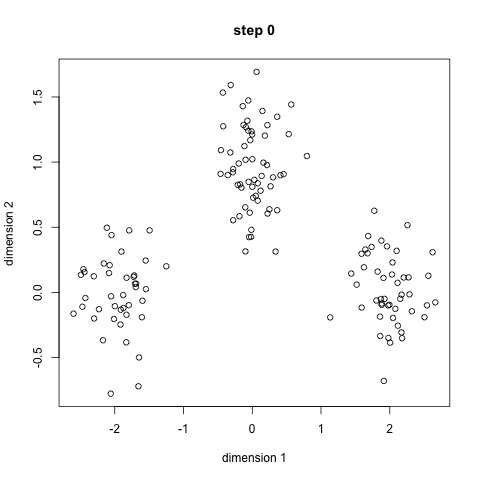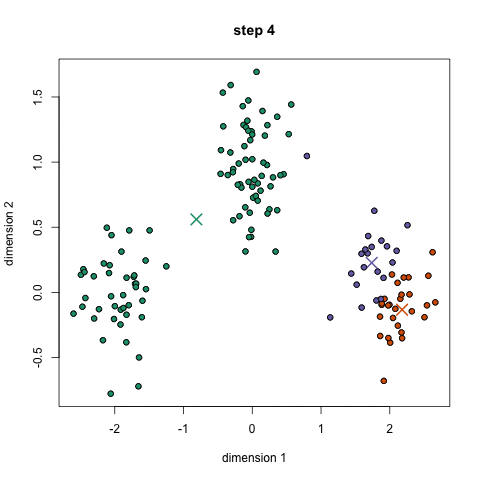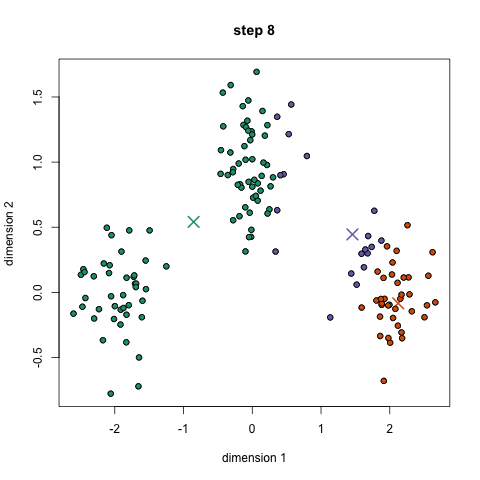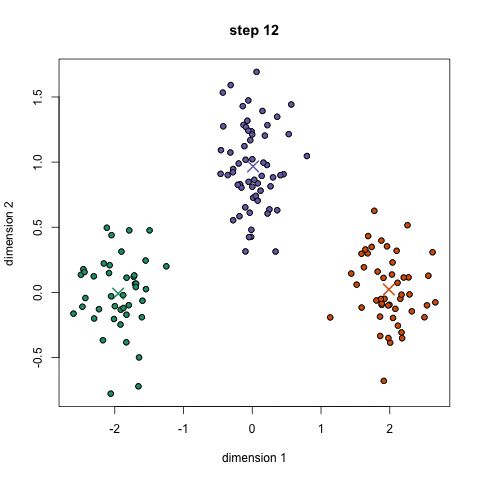
这种方法十分简单易行,不仅好理解而且计算速度很快,对于n个点的图,算法复杂度是的。但缺点也十分明显,只能知道是哪一类的,不知道属于这类的具体概率;而且同样我们不知道到底要聚成多少类比较好。
四.层次凝聚聚类
这种聚类的原理就是,改为自底向上进行聚类,同时将聚类的信息存储在二叉树中。步骤如下:
1.从目前的图中找到距离最小的两个点,当然这个距离也是自己去定义的,之后把这个点作为树的两个叶节点,然后去掉这两个点,加入一个点作为新类。注:新加入的点并不是这两个点的算数平均,因为这两个点也可能是经过了不同数量的原始点的聚类得到的;应是按照这两个点所谓的代表着原始点的数量来进行加权平均。这时如果之剩下一个点则算法结束,聚类完成。
2.计算图中剩下所有的点到这个新点的距离,重复步骤1。
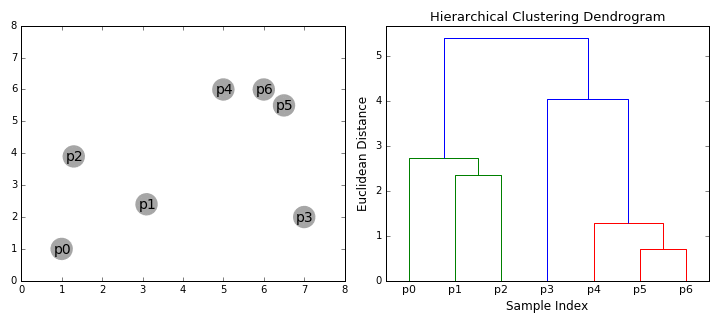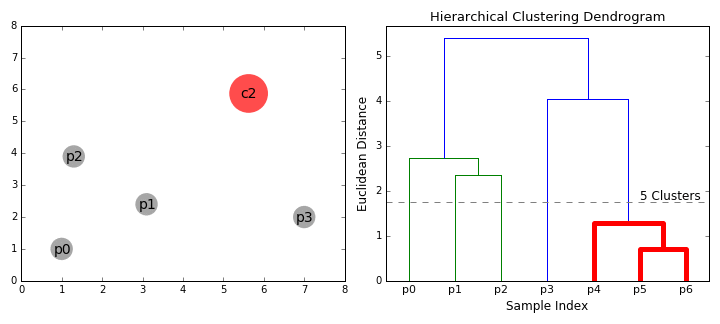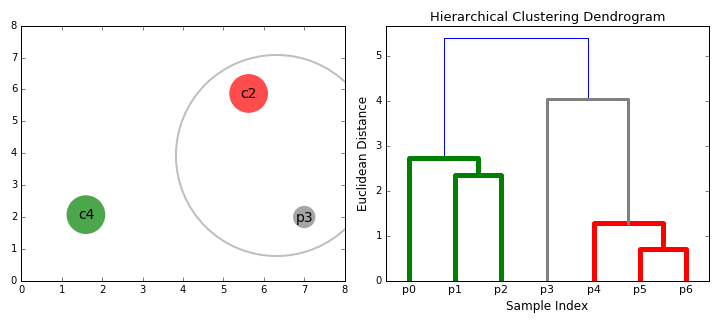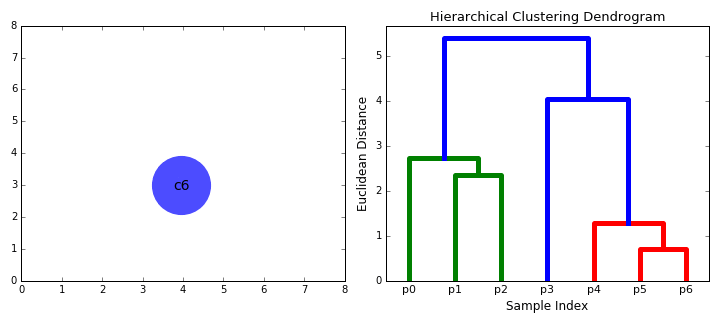
这样做其实我们操作完之后,想聚成多少类都是十分容易计算出结果的,因此可以抵消一部分由于我们不知道类别数量带来的负面影响。当然,这样做其实是一种暴力式的做法。我们最开始要计算个距离,加上后续点的加入,我们一共要计算
个距离。在这n次中都是从
个距离中选出最小的,因此时间复杂度达到了O(n^2),由于要存储树状信息,因此额外需要
的复杂度。实际操作起来会很慢。
五.DBSCAN聚类法
的值,一个是MinPts的值。

动图如下图所示。
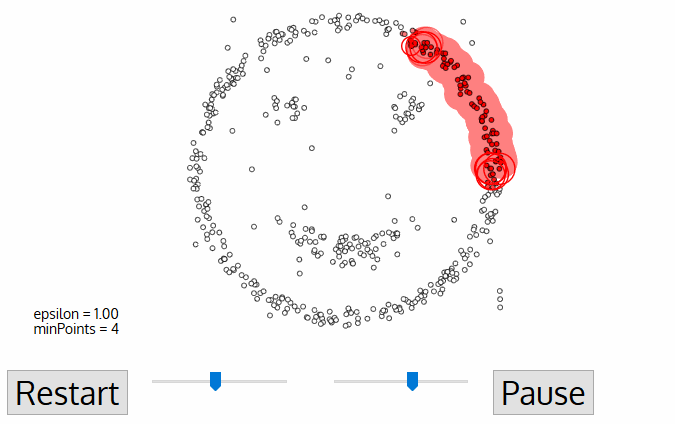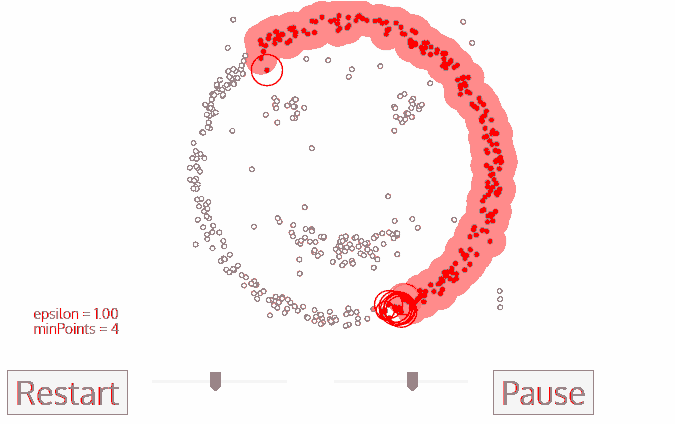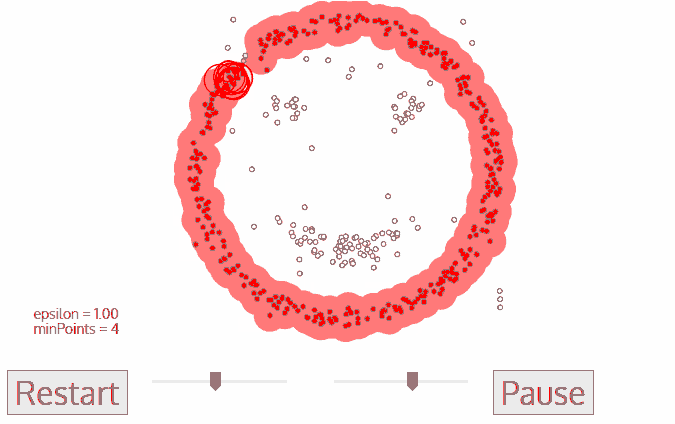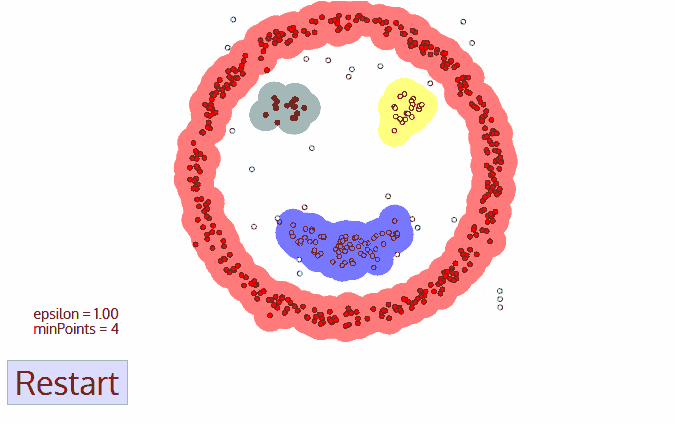
的时间就可以完成。
但这样做的缺点也很明显:我们基于了每个类之中都比较密集,而类与类的边界处数据量很少的特点;对于不符合这种特点的数据集来说,这种方法完全不适用。同时两个超参数的选择可能也会对结果有很大的影响,现实中可能要多取几个数值来多做几次聚类,查看效果。





















